模型推理一文看懂Img2Col卷积加速算法

Posted 2021-07-22 极智视界

  本教程详细解释了直接卷积计算与Img2Col卷积加速算法的实现原理。

1、直接卷积计算

  直接卷积计算一定是很直接的，也是大多数人学习卷积神经网络时所直观了解的卷积计算方式。

  直接卷积是按照卷积层的计算特性进行计算，卷积核中的权重矩阵在经过补零后的输入特征图中滑动，每次在输入特征图中会划出一个与权重矩阵大小一致的子矩阵与之进行对应元素的相乘并累加(点积运算)。

  具体来讲，对于只有一个通道的输入特征图矩阵 X(5 x 5)，现在共有两个卷积核，其中卷积核1的权重为 W1，b1偏置中的所有元素为0；卷积核2的权重为 W2，b2偏置中的所有元素为1；两个卷积核的权重都是 3 x 3 的矩阵，卷积核移动的步长为2，pad 为1。

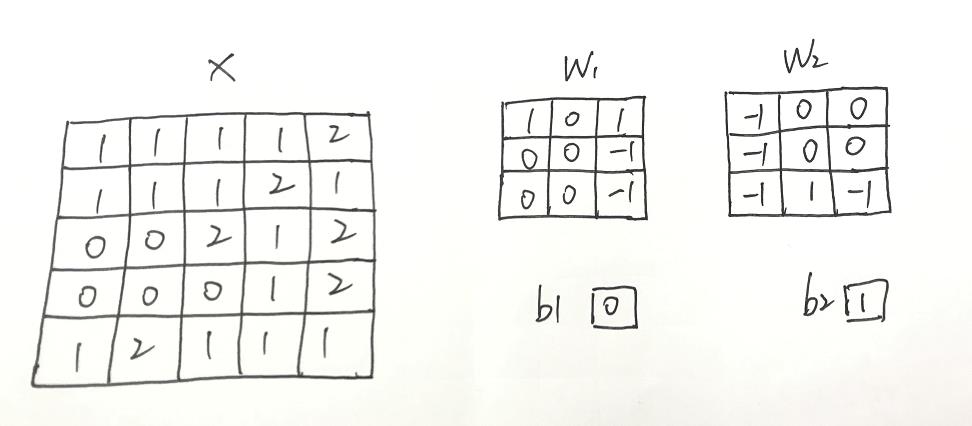
​  进行卷积计算时，首先对于输入特征矩阵 X 进行pad补零，由于pad 为1，故将特征矩阵向外延伸一圈，得到矩阵 Xp。

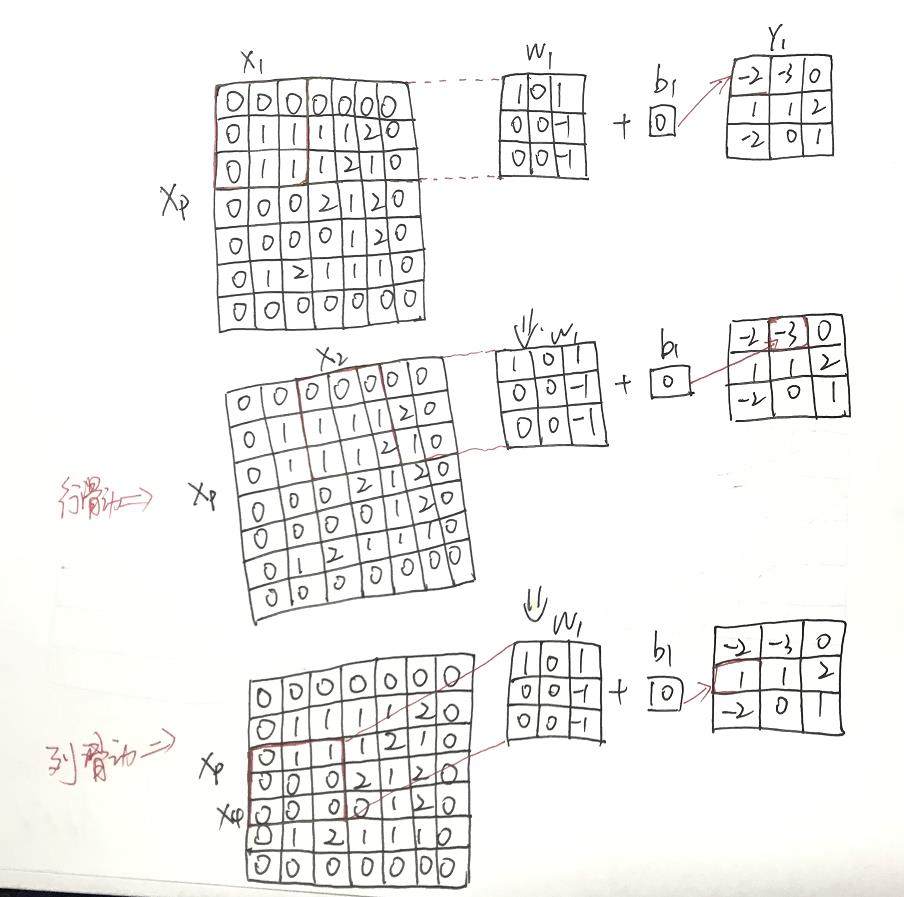
​  正式计算时，权重 W1 在 Xp 矩阵中的初始位置 X1 开始计算，将权重元素与 Xp 中输入特征子矩阵 X1 处的所有元素进行对应的点积操作，再加上偏置后得到输出特征矩阵 Y1 的第一个元素的值 -2，其计算过程是：0 x 1 + 0 x 0 + 0 x 1 + 0 x 0 + 1 x 0 + 1 x (-1) + 0 x 0 + 1 x 0 + 1 x (-1) + 0 = -2。计算完成 Y1 的第一个元素后开始行滑动计算，权重 W1 矩阵向右滑动2个元素的步长，这时权重 W1 与 矩阵 Xp 中输入特征子矩阵 X2 重叠，进行对应元素的点积并加上偏置，得到输出特征矩阵 Y1 的第二个元素的值 -3。以此类推，完成输出特征矩阵 Y1 的第一行的所有元素的计算。在进行 Y1矩阵第二行的元素计算时，权重 W1 从输入特征子矩阵 X1 的位置垂直向下滑动 2个元素的步长，计算输出特征矩阵 Y1 中第二行的第一个元素值 1。卷积核移动的步长在输入特征图中的横向和纵向移动上都发挥着作用。由此经过9次的权重与输入特征子矩阵的点积运算后，得到输出特征图 Y1 的所有元素值。对于卷积核2可使用同样方法得到输出特征图 Y2。

​  至此，通过直接卷积的方式完成了输入特征图和权重矩阵的卷积计算，在实际中，每个卷积核有多个通道，需要使用每一卷积核中一个通道上的权重矩阵对同一通道中输入特征图进行卷积运算，完成该卷积核中所有通道的卷积运算后再把所有通道的结果累加起来作为该卷积核的最终输出特征图。

2、Img2Col 卷积加速算法

​  Img2Col 是通过矩阵乘法来实现卷积，这种方法被广泛应用在 CPU、GPU等一些具有通用编程性的计算芯片上。

​  首先将卷积层中的输入特征图和卷积核权重矩阵展开，然后将卷积中输入特征子矩阵和权重矩阵对应元素的点积操作转换成矩阵运算中行与列向量的乘加运算，这样就能够将卷积层中的大量卷积计算转换成矩阵运算本身的并行度。因此，处理器中只需要高效地实现矩阵乘法，就能够高效的进行卷积运算。CPU 和 GPU 都提供专门的基本线性代数程序集库(BLAS) 来高效的实现向量和矩阵运算。

​  Img2Col 的展开方法是将每一个输入特征子矩阵展开成一行 (也可以是一列)，生成新的输入特征矩阵，其行数和输入特征子矩阵的个数相同。同时将卷积核中的权重矩阵展开成一列 (也可以是一行)，多个权重矩阵可以排列成多列。

​  将输入特征图 Xp 通过 Img2Col 展开成新的矩阵 XI2c 的第一行，输入特征子矩阵 X2 展开成第二行，因为共有9个输入特征子矩阵，所有以此方法展开成 9 行，并生成最终的 XI2c 矩阵。同理，可将第 2 个卷积核的权重矩阵 W1、W2 按照列展开成矩阵 WI2c，偏置量矩阵 bI2c 也可以同样展开得到。接下来进行矩阵乘法运算，将 XI2c 的第1行 与 WI2c的第一列进行计算，再加上偏置便可得到 YI2c 的第1个元素值，依次计算下去得到整个输出特征矩阵 YI2c。

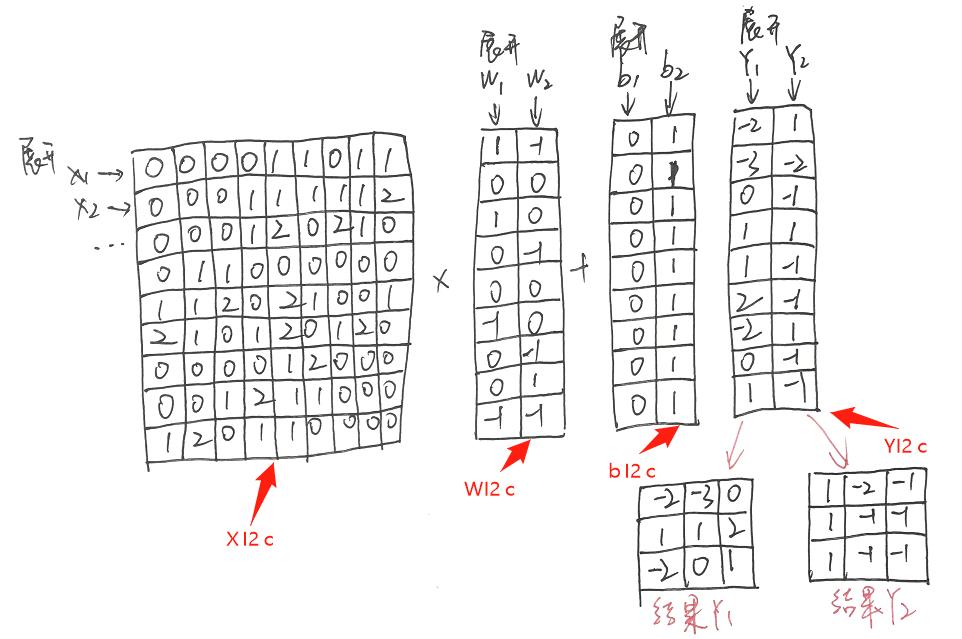
​  Img2Col 的作用就是将卷积通过矩阵乘法来计算，从而能在计算过程中将需要计算的特征子矩阵存放在连续的内存中，有利于一次将所需要计算的数据直接按照需要的格式取出进行计算，这样便减少了内存访问的次数，从而减小了计算的整体时间。而直接卷积计算时，由于输入特征子矩阵存放在内存中地址有重叠且不连续的空间上，在计算时有可能需要多次访问内存。由于多次访问内存直接增加了数据传输时间，从而进一步影响了卷积计算速度，因此 Img2Col 在卷积加速计算中起着促进作用，为卷积计算转换成矩阵乘法提供了必要的基础。

​  若卷积核偏置值为常数时，还可以对加偏置的计算进行优化。将偏置值和卷积核的权重矩阵进行合并，在输入特征矩阵中添加系数，直接通过矩阵乘法一次性实现矩阵乘法和累加偏置的计算。

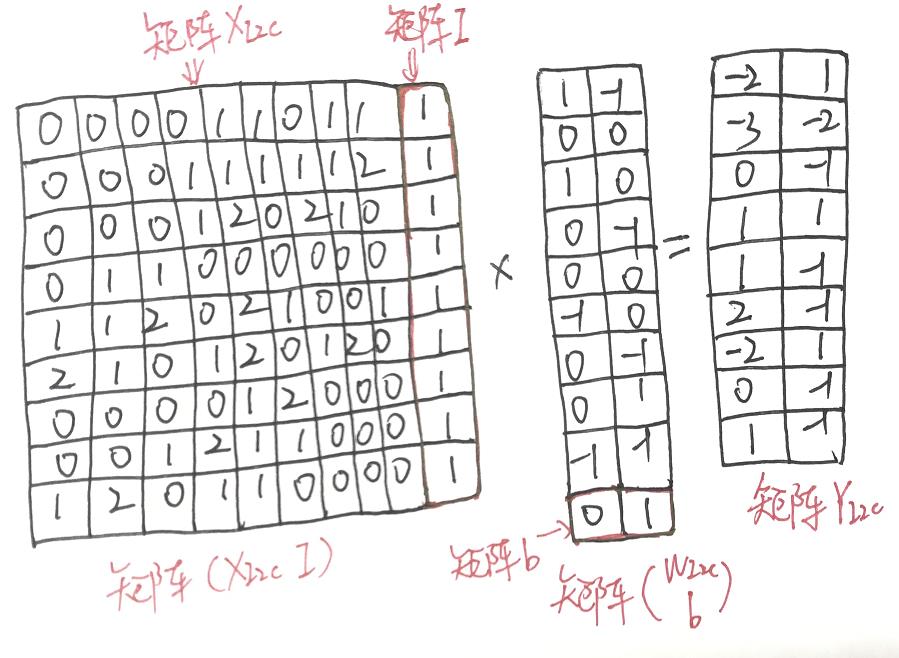
​  在 XI2c 矩阵添加系数矩阵 I，I 矩阵为 9 x 1 矩阵且其元素全为 1；在 WI2c 矩阵中添加偏置矩阵 b，其中 b = [0 1]。则计算公式为：

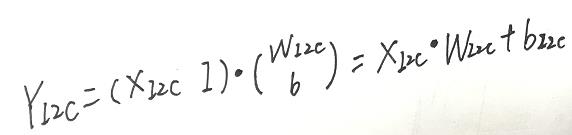
​  通过增加矩阵的维度，可以仅仅使用矩阵乘法进行计算，在硬件上节省了计算资源，简化了计算步骤。

​  增加矩阵的维度，可以仅仅使用矩阵乘法进行计算，在硬件上节省了计算资源，简化了计算步骤。

​  现代处理器中卷积还可以通过诸如快速傅里叶变换 (FFT) 和 Winograd 算法等其他方式实现，后面也会专门写文章来进行介绍。这些方式都是将复杂的卷积运算等价变换成另一个空间的简单运算，从而降低了计算复杂度。值得一提的是，英伟达公司提供的 cuDNN 库中的卷积部分就是使用了 Winograd 算法。一般在卷积神经网络中，卷积层的参数量和计算量占了整个网络的绝大多数，因此合理加速卷积层的计算能够极大提升整个网络的计算速度和系统的执行效率。

扫描下方二维码即可关注我的微信公众号【极智视界】，获取更多AI经验分享，让我们用极致+极客的心态来迎接AI ！