理论+实践史上最全-论文中常用的图像分割评价指标-附完整代码

Posted 2021-07-21 Tina姐

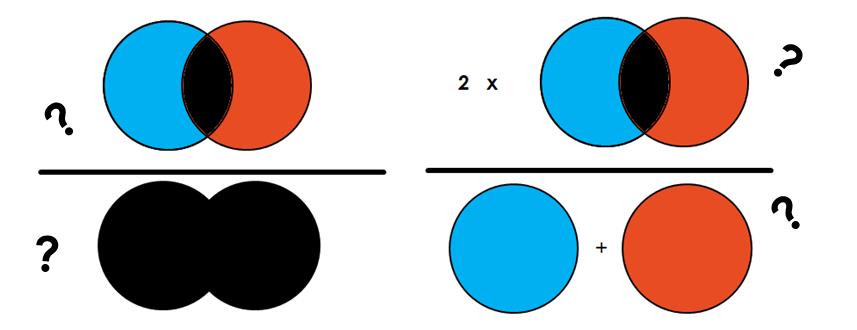
图像分割的评价指标非常多，论文中常用的包括像素准确率(Pixel Accuracy, PA)、交并比(Intersection-Over-Union，IOU)、Dice系数(Dice Coeffcient), 豪斯多夫距离（ Hausdorff distance，HD95），体积相关误差（relative volume error, RVE）。

文末还为懒癌星人提供一站式服务，只需修改地址，就可以实现所有指标，并且将结果存为Excel。

接下来，一一为大家解答。内容超多，建议收藏，需要用到时再来学习。

文中所有案例均是二分类，label中只有0和1

文章目录

• 1 像素准确率
• • 1.1 理论
  • 1.2 代码中如何表达
• 2 交并比 IoU
• • 2.1 理论
  • 2.2. 代码中如何表达
• 3 骰子系数Dice
• • 3.1 原理
  • 3.2 代码中如何实现
• 4 表面距离计算
• • 4.1 Hausdorff distance 豪斯多夫距离
  • 4.2 代码如何实现$H{D}_{95}$和ASD
• 5 相关体积误差 RVE
• 6 为懒癌星人进行打包服务

1 像素准确率

1.1 理论

定义： 它是图像中正确分类的像素百分比。即分类正确的像素占总像素的比例。用公式可表示为：
$$PA=\frac{{\sum }_{i=0}^n{p}_{ii}}{{\sum }_{i=0}^n{\sum }_{j=0}^n{p}_{ij}}=\frac{TP+TN}{TP+TN+FP+FN}$$

其中：

• n : 类别总数，包括背景的话就是n+1
• $p_{ii}$: 真实像素类别为 $i$ 的像素被预测为类别 $i$ 的总数量，就是对于真实类别为 $i$ 的像素来说，分对的像素总数有多少。
• $p_{ij}$: 真实像素类别为 $i$ 的像素被预测为类别 $j$ 的总数量， 换句话说，就是对于类别为 $i$ 的像素来说，被错分成类别 $j$ 的数量有多少。
• TP： 真阳性数，在label中为阳性，在预测值中也为阳性的个数
• TN： 真阴性数， 在label中为阴性，在预测值中也为阴性的个数
• FP： 假阳性数， 在label中为阴性，在预测值中为阳性的个数
• FN： 假阴性数， 在label中为阳性，在预测值中为阴性的个数

TP+TN+FP+FN=总像素数
TP+TN=正确分类的像素数

因此，PA 可以用两种方式来计算。

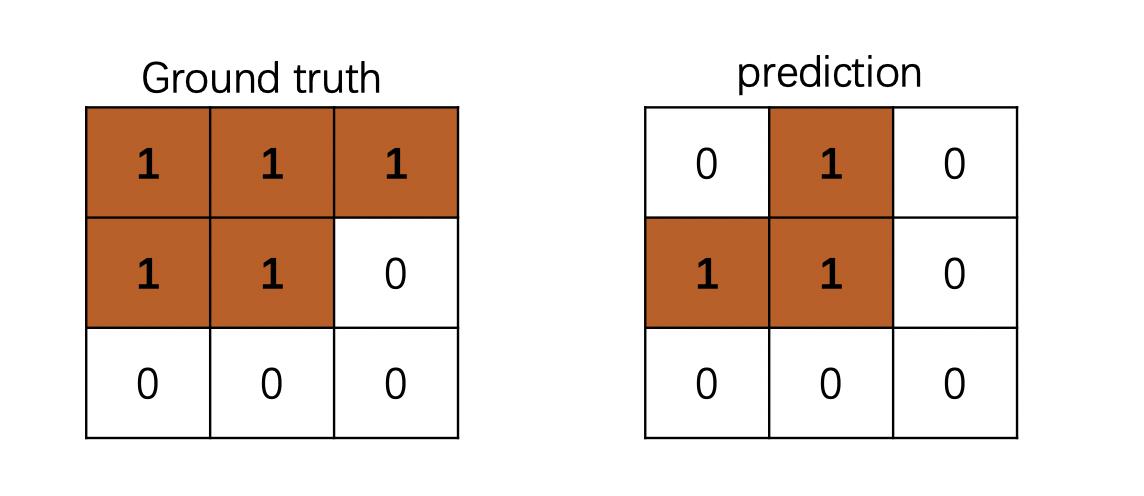
下面使用一个3 * 3 简单地例子来说明： 下图中TP=3,TN=4, FN=2, FP=0

$$PA=\frac{3+4}{3+4+2}=77.8\%$$
即图中正确分类的像素数为7，总像素数为9。

1.2 代码中如何表达

def binary_pa(s, g):
    """
        calculate the pixel accuracy of two N-d volumes.
        s: the segmentation volume of numpy array
        g: the ground truth volume of numpy array
        """
    pa = ((s == g).sum()) / g.size
    return pa
g = np.array([1, 1, 1, 1, 1, 0, 0, 0, 0])
s = np.array([0, 1, 0, 1, 1, 0, 0, 0, 0])
pa = binary_pa(s, g)

是不是就很简单~~~~

这部分还没完。我们继续~~~~~

思考一下，PA很简单，但是，它绝不是最好的指标。

在这个案例中，即使模型什么也没有分割出来，但他的PA = 95%， what？？？

嗯。我们的计算有问题吗？不。完全正确。只是背景类是原始图像的 95%。因此，如果模型将所有像素分类为该类，则 95% 的像素被准确分类，而其他 5% 则没有。

因此，尽管您的准确率高达 95%，但您的模型返回的是完全无用的预测。这是为了说明高像素精度并不总是意味着卓越的分割能力。

这个问题称为类别不平衡。当我们的类极度不平衡时，这意味着一个或一些类在图像中占主导地位，而其他一些类只占图像的一小部分。不幸的是，类不平衡在许多现实世界的数据集中普遍存在，因此不容忽视。

因此，这个指标基本没什么指导意义。

2 交并比 IoU

Intersection-Over-Union (IoU)，也称为 Jaccard 指数，是语义分割中最常用的指标之一……这是有充分理由的。IoU 是一个非常简单的指标，非常有效。

2.1 理论

简单地说，IoU 是预测分割和标签之间的重叠区域除以预测分割和标签之间的联合区域（两者的交集/两者的并集），如图所示。该指标的范围为 0–1 (0–100%)，其中 0 表示没有重叠，1 表示完全重叠分割。

对于二元分类而言，其计算公式为：

$$IoU=\frac{|A\bigcap B|}{|A\bigcup B|}=\frac{TP}{TP+FP+FN}$$

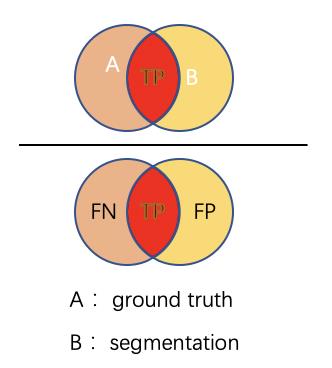
还是上面那个3 * 3 的例子，我们来计算一下它的IoU

$$IoU=\frac{交集=3}{并集=5}=\frac{TP=3}{TP+FP+FN=5}=60\%$$

2.2. 代码中如何表达

# IOU evaluation
def binary_iou(s, g):
    assert (len(s.shape) == len(g.shape))
    # 两者相乘值为1的部分为交集
    intersecion = np.multiply(s, g)
    # 两者相加，值大于0的部分为交集
    union = np.asarray(s + g > 0, np.float32)
    iou = intersecion.sum() / (union.sum() + 1e-10)
    return iou
g = np.array([1, 1, 1, 1, 1, 0, 0, 0, 0])
s = np.array([0, 1, 0, 1, 1, 0, 0, 0, 0])
iou = binary_iou(s, g)
print(iou)

如果理解了原理，代码依然很简单。

tips: 分母中加了一项1e-10， 是为了防止分母为0的情况出错。

3 骰子系数Dice

3.1 原理

定义： Dice系数定义为两倍的交集除以像素和，也叫F1 score。Dice 系数与 IoU 非常相似，它们是正相关的。这意味着如果一个人说模型 A 在分割图像方面比模型 B 更好，那么另一个人也会这么说。

与 IoU 一样，它们的范围都从 0 到 1，其中 1 表示预测和真实之间的最大相似度。

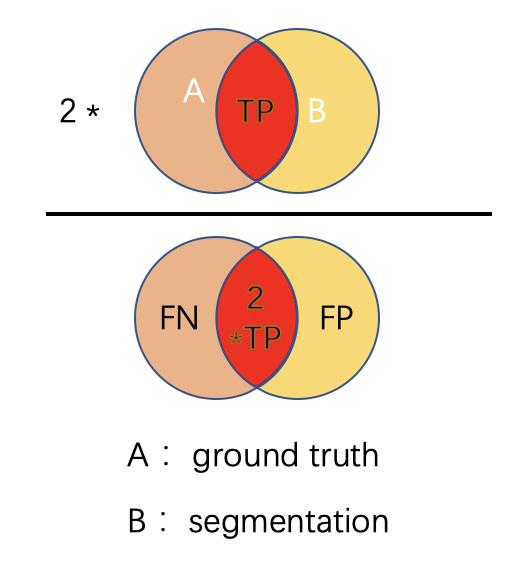
其公式为：

$$Dice=\frac{2|A\bigcap B|}{|A|+|B|}=\frac{2TP}{2TP+FP+FN}$$

可以看到Dice系数对应于IoU，分子分母中的TP都取了两倍

还是上面那个3 * 3 的例子，我们来计算一下它的Dice：

$$Dice=\frac{2\ast 3}{5+3}=\frac{2TP=6}{2TP+FP+FN=8}=75\%$$

3.2 代码中如何实现

def binary_dice(s, g):
    """
    calculate the Dice score of two N-d volumes.
    s: the segmentation volume of numpy array
    g: the ground truth volume of numpy array
    """
    assert (len(s.shape) == len(g.shape))
    prod = np.multiply(s, g)
    s0 = prod.sum()
    dice = (2.0 * s0 + 1e-10) / (s.sum() + g.sum() + 1e-10)
    return dice
g = np.array([1, 1, 1, 1, 1, 0, 0, 0, 0])
s = np.array([0, 1, 0, 1, 1, 0, 0, 0, 0])
dice = binary_dice(s, g)
print(dice)

以上的指标意义可以重点掌握，以下有点难度，看不懂直接拉到最后，抄作业就好~~

4 表面距离计算

当我们评价图像分割的质量和模型表现时，经常会用到各类表面距离的计算。
比如

• Average surface distance 平均表面距离
• Hausdorff distance 豪斯多夫距离
• Surface overlap 表面重叠度
• Surface dice 表面dice值
• Volumetric dice 三维dice值

4.1 Hausdorff distance 豪斯多夫距离

将Hausdorff distance， HD 用于分割指标，主要是用来度量边界的分割准确度

HD 是描述两组点集之间相似程度的一种量度，它是两个点集之间距离的一种定义形式：假设有两组集合A={a1,…,ap},B={b1,…,bq},则这两个点集合之间的HD定义为：

$$H(A,B)以上是关于理论+实践史上最全-论文中常用的图像分割评价指标-附完整代码的主要内容，如果未能解决你的问题，请参考以下文章$$

理论 | 可能是史上最全的weex踩坑攻略

高光谱图像重构常用评价指标及其Python实现

图像分类Swin Transformer理论解读+实践测试

最新最全Diffusion Models论文代码汇总(图像生成图像分割图像翻译超分辨率重建医疗影像自然语言处理视频生生成时间序列生成3D点云生成文本语音转换音频生成等)

语义分割评价指标(Dice coefficient, IoU)

认知控制和执行功能常用的实验范式（史上最全）