蓝桥杯——动态规划专题

Posted 2021-07-21 中二病没有蛀牙

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了蓝桥杯——动态规划专题相关的知识，希望对你有一定的参考价值。

集合划分原则：不重不漏，找最后一个不同点

整数划分问题

例题鸣人的影分身

https://www.acwing.com/problem/content/description/1052/
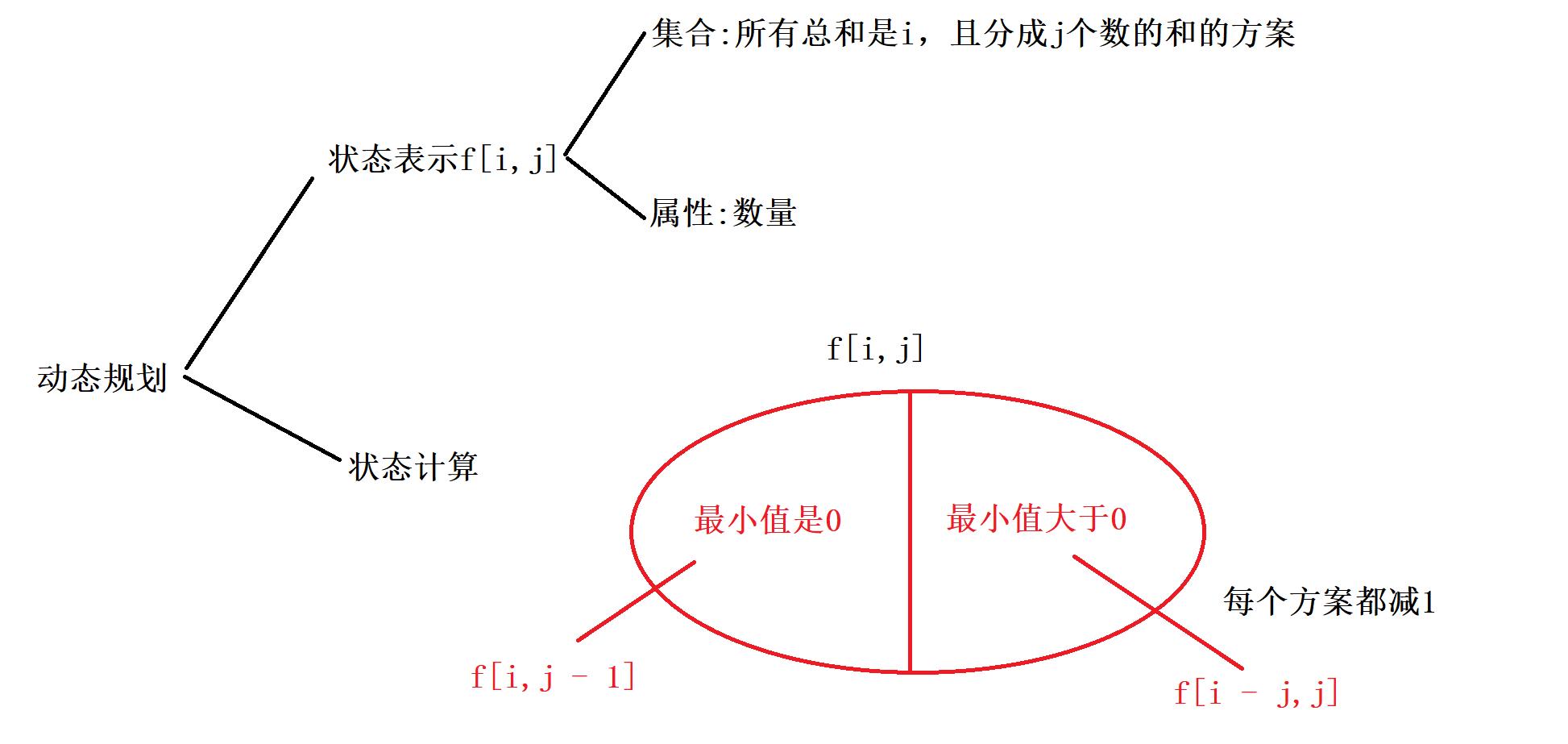
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1005;
int f[maxn][maxn];
int main()
{
    int t,m,n;
    cin>>t;
    while(t--){
        memset(f,0,sizeof(f));
        f[0][0] = 1;

        cin>>m>>n;
        for(int i = 0; i <= m; ++i){
            for(int j = 1;j <= n; ++j){
                f[i][j] = f[i][j - 1] ;
                if(i >= j) f[i][j] += f[i - j][j];
            }
        }
        cout<<f[m][n]<<endl;
    }
    return 0;
}

选择( 背包)

例题糖果

链接：https://www.acwing.com/solution/content/10497/

状态表示： f[i][j]

集合：从i个数中选总和模k为j的方案
属性：最大值

状态计算： ---- 集合的划分
划分依据：是否包含第i个数

包含第i个数 ---- f[i - 1, j - w % k] + w
不包含第i个数 ---- f[i - 1][j]

代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 105;
int f[maxn][maxn];
int a[maxn];


int main()
{
    int n,k;
    cin>>n>>k;
    for(int i = 1;i <= n;i++){
        cin>>a[i];
    }

    memset(f,-0x3f,sizeof(f));
    f[0][0] = 0;
    for(int i = 1;i <= n; ++i){
        for(int j = 0;j < k;j++){
            f[i][j] = max(f[i -1][j],f[i - 1][(j - a[i] % k + k) % k] + a[i]);
        }
    }
    cout<<f[n][0]<<endl;
    return 0;
}

完全背包

例题：包子凑数
https://www.acwing.com/problem/content/description/1228/

结论是如果所有的数的最大公约数不为1，就有不能凑出的数，并且小于10000，否则就有无限个

这个过程用完全背包求解
在这里插入图片描述

代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 105;
#define INF 0x3f3f3f3f
typedef long long ll;
typedef pair<int,int> PII;
int a[maxn];
int f[maxn][10005];
int  gcd(int m,int n)
{
    if(n == 0) return m;
    return gcd(n,m%n);
}
int main()
{   
    int n,cnt;
    cin>>n;
    for(int i = 1; i <= n; ++i){
        cin>>a[i];
        if(i != 1){
            cnt = gcd(a[i],cnt);
        }
        else cnt = a[1];
    }
    if(cnt != 1){
        cout<<"INF"<<endl;
        return 0;
    }
    f[0][a[1]] = 1;
    for(int i = 1;i <= n;i++){
        for(int j = 0;j <= 10005;j++){
            f[i - 1][0] = 1;
            if(f[i - 1][j] == 0) continue;
            f[i][j] = f[i -1][j];
            for(int k = 1;j + k*a[i] <= 10005;k++)
                f[i][j + k*a[i]] = f[i-1][j];
        }
    }
    int ans = 0;
    for(int i = 1;i <= 10000; i++){
        if(!f[n][i]) {
            // cout<<i<<endl;
            ans++;
        }
    }
    cout<<ans<<endl;
    return 0;
}

区间dp

区间dp循环的时候可以先循环区间的长度

例题密码脱落

https://www.acwing.com/problem/content/1224/

增加的就是原字符中中不是回文序列的字符的数量

一. 状态表示

l,r之间的回文子序列的长度

二. 状态划分

L,R都在集合里
f[l+1,r-1] + 2
L在集合里
f[l,r-1]
R在集合里
f[l+1,r]
L,R都不在集合里
f[l+1,r-1]

区间dp循环的时候可以先循环区间的长度

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1005;
int f[maxn][maxn];
#define INF 0x3f3f3f3f
int main()
{
    string ss ;
    cin >> ss ;
    //memset(f,-INF, sizeof(f));
    f[0][0] = 0;
    for(int len = 1; len <= ss.length() ; ++len) {
        for(int l = 0; l < ss.length(); l++)  {
            int r = l + len -1;
            if(len == 1) {
                f[l][r] = 1;
                continue;
            }
            if(ss[l] == ss[r]) 
                f[l][r] = f[l + 1][ r - 1] + 2;
            f[l][r] = max(f[l][r],f[l][r - 1]);
            f[l][r] = max(f[l][r], f[l + 1][r]);
            // cout<<f[l][r]<<endl;
        }
    }
    cout<<ss.length() - f[0][ss.length() - 1] <<endl;
    return 0;
}

树形dp

#include <bits/stdc++.h>
using namespace std;
const int maxn = 100005;
#define INF 0x3f3f3f3f
typedef long long ll;
ll f[maxn];
ll a[maxn];
vector<ll> g[maxn];

void dfs(int u,int fa){
    f[u] = a[u];
    for(auto v:g[u]){
        // cout<<v<<endl;
        if(v == fa ) continue;
        dfs(v,u); 
        f[u] = max(f[u],f[u] + f[v]);
        // cout<<f[u]<< " "<<f[v]<<endl;
    }
}

int main()
{
    int n;
    cin>>n;
    for(int i = 1;i <= n; ++i)
        cin>>a[i];
    int u,v;
    // memset(f,-INF,sizeof(f));
    for(int i = 1;i <= n - 1; ++i )  {
        cin>>u>>v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    dfs(1,0);
    ll ans = -INF;
    for(int i = 1;i <= n; i++)
        ans = max(ans,f[i]);
    cout<<ans<<endl;
    return 0;
}