Java算法之任意阶矩阵的顺时针打印数据

Posted 2021-07-21 笔触狂放

        作为一个IT工程师，开发任何一款软件，不管是BS结构项目还是CS结构项目，还是移动端项目，算法才是核心，怎么处理数据，达到某种效果，完成某个功能，增强软件的安全性，加快项目的运行速度，提高应用的性能等等问题都是算法。

        算法是一种数学逻辑思维能力运用在不同的计算机编程语言上。

        那么先理解一下题意，看图:

        

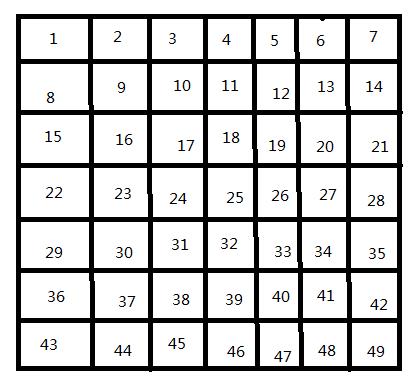
顺时针打印流程:

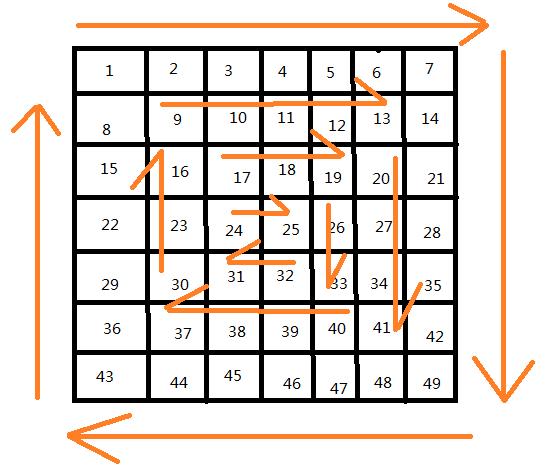
最后的结果应该得到:1 2 3 4 5 6 7 14 21 28 35 42 49 48 47 46 45 44 43 36 29 22 15 8 9 10 11 12 13 14 2128 35 42 41 40 39 38 37 30 23 16 17 18 19 20 27 34 33 32 31 24 25

题目我们应该清楚了，那么算法题的最要的步骤就是分析的解题思路，我们做了多年的数学题，应该非常清楚，正确的解题思路才能快速的完成做题。接下来看解题思路:

解题思路:
 * 1.先获得该二维数组的左上角的横纵坐标点和右下角的横纵坐标点
 * 2.设置移动的坐标点
 * 3.让移动的坐标点开始从左往右移动，也就是横坐标不动，纵坐标自增，但不能超出边界
 * 4.移动的坐标移动到最右边后，开始向下移动，先把移动的坐标的列改变为最后一列的值
 * 5.让移动的坐标点开始从上往下移动，也就是纵坐标不动，横坐标自增，但不能超出边界
 * 6.移动的坐标移动到最后一行后，开始向左移动，先把移动的坐标的行改变为最后一行的值
 * 7.让移动的坐标点开始从右往左移动，也就是横坐标不动，纵坐标自减，但不能超出边界
 * 8.移动的坐标移动到最左边后，开始向上移动，先把移动的坐标的行改变为最后一行的值
 * 9.让移动的坐标点开始从下往上移动，也就是纵坐标不动，横坐标自减，但不能超出边界
 * 10.移动的坐标走完最外层一圈后，把二维数组进行缩小，把走完的数据剔除掉，然后再按照步骤循环开始走
 * 11.在循环的过程中避免起点坐标和终点坐标的位置调换，需要加上判断，起点坐标只能小于等于终点坐标

接下来看代码:

package com.lqb2021;

import java.util.Scanner;

public class T4_1 {
	
	private int[][] nums=null;
	
	private void init() {
		Scanner scanner=new Scanner(System.in);
		System.out.println("请输入二维数组的阶数:");
		int n=scanner.nextInt();
		scanner.close();
		nums=new int[n][n];
		int num=1;
		for (int i = 0; i < nums.length; i++) {
			for (int j = 0; j < nums[i].length; j++) {
				nums[i][j]=num++;
				System.out.print(nums[i][j]+"\\t");
			}
			System.out.println();
		}

		print();
	}
	
	private void print() {
		System.out.println("结果为:");
		//设置二维数组移动的范围坐标点
		int left_up_x=0,left_up_y=0,right_down_x=nums.length-1,right_down_y=nums[0].length-1;
		//循环一圈圈打印
		while (left_up_x<=right_down_x&&left_up_y<=right_down_y) {
			//设置移动的坐标点
			int x=left_up_x,y=left_up_y;
			//开始横向移动
			while (y<=right_down_y) {
				System.out.print(nums[x][y++]+" ");
			}
			y=right_down_y;
			x++;
			//向下移动
			while (x<=right_down_x) {
				System.out.print(nums[x++][y]+" ");
			}
			x=right_down_x;
			y--;
			//向左移动
			while (y>=left_up_y) {
				System.out.print(nums[x][y--]+" ");
			}
			y=left_up_y;
			x--;
			//向上移动
			while (x>left_up_x) {
				System.out.print(nums[x--][y]+" ");
			}
			x=left_up_x;
			//打印完一圈，起点坐标和终点坐标发生变化
			left_up_x++;left_up_y++;right_down_x--;right_down_y--;
		}
		
	}
	

	public static void main(String[] args) {
		new  T4_1().init();

	}

}

接下来看第二种解法:

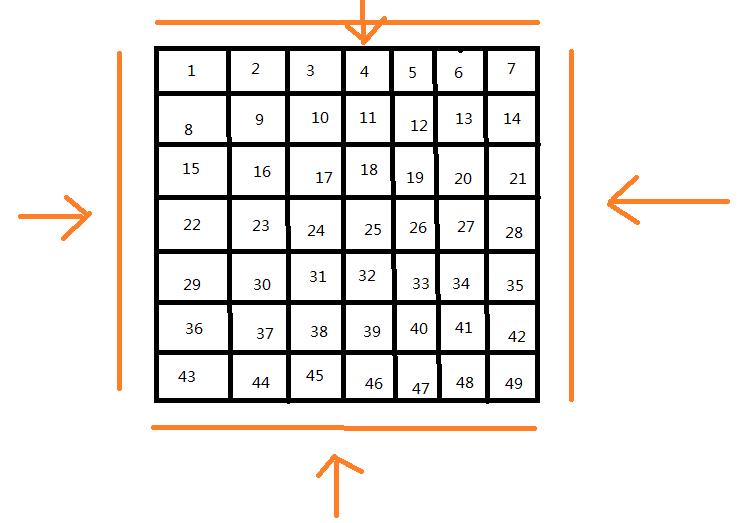
给该矩阵设定四个变量，分别用于控制四条边的下标，当第一行输出完后，上边变量加一，往里面缩进一行，接下来走右边往下走，当最后一列输出完，右边变量减一，往里面缩进一列，然后下边开始输出数字，输出完，下边变量减一，往里面缩进一行，左边开始输出，输出完，左边变量加一，往里面缩进一列，以此类推也能完成该题的效果，并且这种方式降低了程序运行的时间复杂度和空间复杂度。

看代码:

public class CopyOfErweiDemoo {
	public static void main(String[] args) {
		/*int[][] arr = { { 1, 2, 3, 4, 5 }, { 6, 7, 8, 9, 10 },
				{ 11, 12, 13, 14, 15 }, { 16, 17, 18, 19, 20 } };
		print(arr);*/
		init();
	}

	private static void print(int[][] Erivl) {
		int Z = 0, S = 1;
		int X = Erivl.length - 1;
		int Y = Erivl[0].length - 1;
		int m = 0, n = 0;
		boolean boo = true;
		while (Z <=Y && S <= X) {
			if (boo) {
				System.out.print(Erivl[m][n]+" ");
				if (n < Y) {
					n++;
				} else if (m < X) {
					m++;
				} else {
					boo = !boo;
					--Y;--X;n--;
				}
			} else {
				System.out.print(Erivl[m][n]+" ");
				if (n >Z) {
					n--;
				} else if (m > S) {
					m--;
				} else {
					boo = !boo;
					++Z;++S;n++;
				}

			}
		}
		System.out.println(Erivl[m][n]+" ");
	}

	private static int[][] nums = null;

	private static void init() {
		System.out.println("请输入二维数组的阶数:");
		Scanner scanner = new Scanner(System.in);
		int n = scanner.nextInt();
		scanner.close();
		nums = new int[n][n];
		int num = 1;
		for (int i = 0; i < nums.length; i++) {
			for (int j = 0; j < nums[i].length; j++) {
				nums[i][j] = num++;
				System.out.print(nums[i][j] + "\\t");
			}
			System.out.println();
		}
		System.out.println("结果为:");
		print(nums);
	}
}

思路清晰了，代码的流程也就非常清楚了，供大家学习和参考，迈进算法的大门。

该题在生活中也在被广泛使用，就是LED灯上的跑马灯效果。

如果大家对于这个算法题理解了，那么大家尝试生成任意矩阵然后进行逆时针打印输出。如果觉得矩阵数据量比较大，可以先生成阶数比较小点的矩阵完成效果。