优化算法鸽群优化算法（PIO）含Matlab源码 1077期

Posted 2021-07-20 紫极神光（Q1564658423）

一、简介

2014 年 段 海 滨 教 授 通 过 归 纳 总 结 ， 提 出 鸽 群 算 法（Pigeon-inspired Optimization PIO），PIO 是模拟鸽子归巢行为而设计出来的群智能优化算法。PIO 具有原理简明的特点、需要调整参数极少、易于被实现。与其他算法比较有着计算相对简单，鲁棒性相对较强等明显的优点。
算法原理
鸽子在距离目的地较远时，是在地磁场和地标建筑的帮助下到达目的地。影响鸽群归巢的关键原因可分为 3 类,第一个原因是太阳，第二个原因是地球的磁场，第三个原因是地貌景观,而鸽子在飞行的过程中，根据不同的情况会使用不同的巡航工具。首先通过地磁场来对一个大概的方向进行辨别，然后利用地貌景象对目前的方向实施修正，直到到达精确的目的地。所以 PIO 算法中鸽子归巢有两个基本部分组成：指南针算子和地标算子。当鸽子距离自己目的地较远时是利用地磁场来辨别方向，当距离目的地比较近时就利用当地地标来进行导航。在 PIO 中地图和指针算子模型的提出就是基于地磁场和太阳，而地标算子模型的提出是基于地标。

** 指南针算子**

地标算子

二、源代码

%_________________________________________________________________________%
% 鸽群优化算法             %
%_________________________________________________________________________%

% 使用方法
%__________________________________________
% fobj = @YourCostFunction        设定适应度函数
% dim = number of your variables   设定维度
% Max_iteration = maximum number of generations 设定最大迭代次数
% SearchAgents_no = number of search agents   种群数量
% lb=[lb1,lb2,...,lbn] where lbn is the lower bound of variable n  变量下边界
% ub=[ub1,ub2,...,ubn] where ubn is the upper bound of variable n   变量上边界
% If all the variables have equal lower bound you can just
% define lb and ub as two single number numbers

% To run PIO: [Best_pos,Best_score,curve]=PIO(pop,Max_iter,lb,ub,dim,fobj)
%__________________________________________

clear all 
clc
% rng('default');
SearchAgents_no=50; % Number of search agents 种群数量

Function_name='F9'; % Name of the test function that can be from F1 to F23 (Table 1,2,3 in the paper) 设定适应度函数

Max_iteration=1000; % Maximum numbef of iterations 设定最大迭代次数

% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);  %设定边界以及优化函数

[Best_score,Best_pos,PIO_curve]=PIO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj); %开始优化
% This function containts full information and implementations of the benchmark 
% lb is the lower bound: lb=[lb_1,lb_2,...,lb_d]
% up is the uppper bound: ub=[ub_1,ub_2,...,ub_d]
% dim is the number of variables (dimension of the problem)

function [lb,ub,dim,fobj] = Get_Functions_details(F)


switch F
    case 'F1'
        fobj = @F1;
        lb=-100;
        ub=100;
        dim=30;
        
    case 'F2'
        fobj = @F2;
        lb=-10;
        ub=10;
        dim=30;
        
    case 'F3'
        fobj = @F3;
        lb=-100;
        ub=100;
        dim=30;
        
    case 'F4'
        fobj = @F4;
        lb=-100;
        ub=100;
        dim=30;
        
    case 'F5'
        fobj = @F5;
        lb=-30;
        ub=30;
        dim=30;
        
    case 'F6'
        fobj = @F6;
        lb=-100;
        ub=100;
        dim=30;
        
    case 'F7'
        fobj = @F7;
        lb=-1.28;
        ub=1.28;
        dim=30;
        
    case 'F8'
        fobj = @F8;
        lb=-500;
        ub=500;
        dim=30;
        
    case 'F9'
        fobj = @F9;
        lb=-5.12;
        ub=5.12;
        dim=30;
        
    case 'F10'
        fobj = @F10;
        lb=-32;
        ub=32;
        dim=30;
        
    case 'F11'
        fobj = @F11;
        lb=-600;
        ub=600;
        dim=30;
        
    case 'F12'
        fobj = @F12;
        lb=-50;
        ub=50;
        dim=30;
        
    case 'F13'
        fobj = @F13;
        lb=-50;
        ub=50;
        dim=30;
        
    case 'F14'
        fobj = @F14;
        lb=-65.536;
        ub=65.536;
        dim=2;
        
    case 'F15'
        fobj = @F15;
        lb=-5;
        ub=5;
        dim=4;
        
    case 'F16'
        fobj = @F16;
        lb=-5;
        ub=5;
        dim=2;
        
    case 'F17'
        fobj = @F17;
        lb=[-5,0];
        ub=[10,15];
        dim=2;
        
    case 'F18'
        fobj = @F18;
        lb=-2;
        ub=2;
        dim=2;
        
    case 'F19'
        fobj = @F19;
        lb=0;
        ub=1;
        dim=3;
        
    case 'F20'
        fobj = @F20;
        lb=0;
        ub=1;
        dim=6;     
        
    case 'F21'
        fobj = @F21;
        lb=0;
        ub=10;
        dim=4;    
        
    case 'F22'
        fobj = @F22;
        lb=0;
        ub=10;
        dim=4;    
        
    case 'F23'
        fobj = @F23;
        lb=0;
        ub=10;
        dim=4;            
end

end

三、运行结果

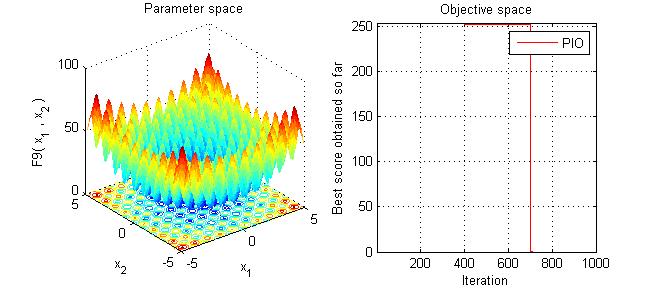
四、备注

版本：2014a