图解二分查找算法 -- python实现

Posted 2021-07-20 TIAP

我们之前介绍过 ，本文介绍一下二分查找算法的原理和实现。

假如我们要在一堆有序列表中查找一个单词：kill, 我们需要怎么做呢？可以从头开始遍历这个列表，一直到找到为止。但是这样的效率可能会比较低，所以我们也可以从中间开始查找，因为我们要查找的这个单词是以 "k" 为开头的，在列表中应该是处于中间位置。再比如我们要找一个以 "o" 开头的单词，也可以从中间开始遍历。

再比如我们要登录某一个系统，系统要核实我们的身份，就会从数据库中查找我们用以登录的用户名，如果登录的用户名是kalli，系统当然可以从头开始查找，但更合理的方法是从中间开始查询。

这是一个查找问题，在前述所有情况下，都可使用同一种算法来解决问题，这种算法就是二分查找。

二分查找是一种算法，其输入是一个有序的元素列表（必须有序的原因稍后解释）。如果要 查找的元素包含在列表中，二分查找返回其位置；否则返回null。

下图是一个例子：

下面的示例说明了二分查找的工作原理。我随便想一个1～100的数字：

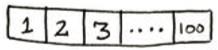
你的目标是以最少的次数猜到这个数字。你每次猜测后，我会说小了、大了或对了。假设你从1开始依次往上猜，猜测的过程会是这样：

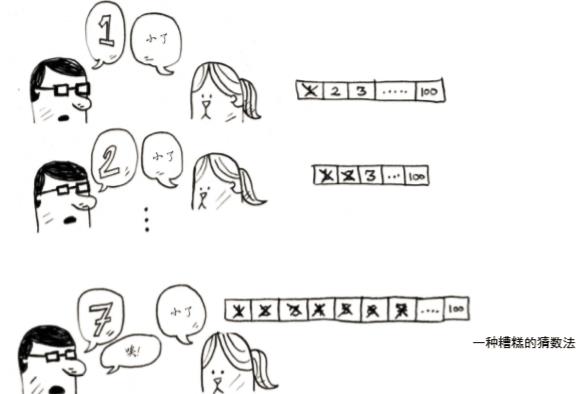
这是简单查找，更准确的说法是傻瓜式查找。每次猜测都只能排除一个数字。如果我想的数字是99，你得猜99次才能猜到！

更好的查找方式

下面是一种更佳的猜法。从50开始。

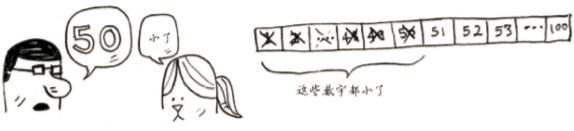
小了，但排除了一半的数字！至此，你知道1～50都小了。接下来，你猜75：

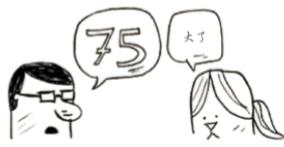
大了，那余下的数字又排除了一半！使用二分查找时，你猜测的是中间的数字，从而每次都将余下的数字排除一半。接下来，你猜63（50和75中间的数字）。

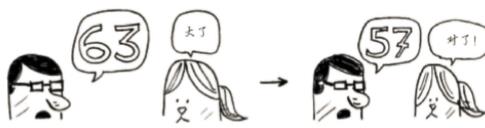
这就是二分查找，你学习了第一种算法！每次猜测排除的数字个数如下：

不管我心里想的是哪个数字，你在7次之内都能猜到，因为每次猜测都将排除很多数字！假设你要在字典中查找一个单词，而该字典包含240000个单词，你认为每种查找最多需要多少步？如果要查找的单词位于字典末尾，使用简单查找将需要240000步。使用二分查找时，每次排除一半单词，直到最后只剩下一个单词。

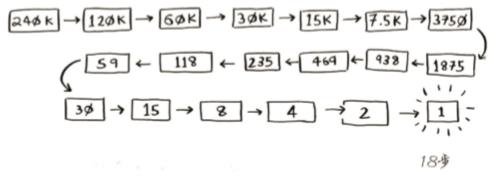
因此，使用二分查找只需18步——少多了！一般而言，对于包含n个元素的列表，用二分查找最多需要log2n步，而简单查找最多需要n步。

对数

你可能不记得什么是对数了，但很可能记得什么是幂。log10100相当于问“将多少个10相乘的结果为100”。答案是两个：10 × 10 = 100。因此，log10100 = 2。对数运算是幂运算的逆运算：

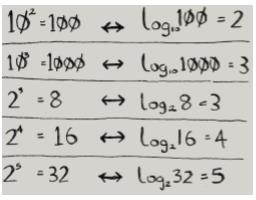
下面来看看如何编写执行二分查找的Python代码。函数binary_search接受一个有序数组和一个元素。如果指定的元素包含在数组中，这个函数将返回其位置。你将跟踪要在其中查找的数组部分——开始时为整个数组：

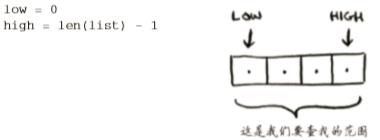
你每次都检查中间的元素：

如果猜的数字小了，就相应地修改low：

如果猜的数字大了，就修改high。完整的代码如下：

#二分查找def binary_search(lst,item): low=0 high=len(lst)-1  while low<=high: mid=int((low+high)/2) guess=lst[mid] if guess==item: return mid if guess > item: high=mid-1 else: low=mid+1 return None

my_list=[1,3,5,7,9]print(binary_search(my_list,3));print(binary_search(my_list,-1));

运行时间

每次介绍算法时，我都将讨论其运行时间。一般而言，应选择效率最高的算法，以最大限度地减少运行时间或占用空间。

回到前面的二分查找。使用它可节省多少时间呢？简单查找逐个地检查数字，如果列表包含100个数字，最多需要猜100次。如果列表包含40亿个数字，最多需要猜40亿次。换言之，最多需要猜测的次数与列表长度相同，这被称为线性时间（lineartime）。

二分查找则不同。如果列表包含100个元素，最多要猜7次；如果列表包含40亿个数字，最多需猜32次。厉害吧？二分查找的运行时间为对数时间（或log时间）。下图（查找算法的运行时间）总结了我们发现的情况：