看了这篇博客,再也不害怕别人问我把不把握得住数据存储了(初)
Posted Aline2021-yxz
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了看了这篇博客,再也不害怕别人问我把不把握得住数据存储了(初)相关的知识,希望对你有一定的参考价值。
初学C语言的小伙伴们可能多数认为指针是C语言的重点,其实这只是表象,“内存”才是本质,学不好内存,C语言等于没学。
内存如此重要,本篇博客就带大家来学习数据在内存中是如何存储的。
数据在内存中的存储
认识内存
我们可以将内存想象为这样:
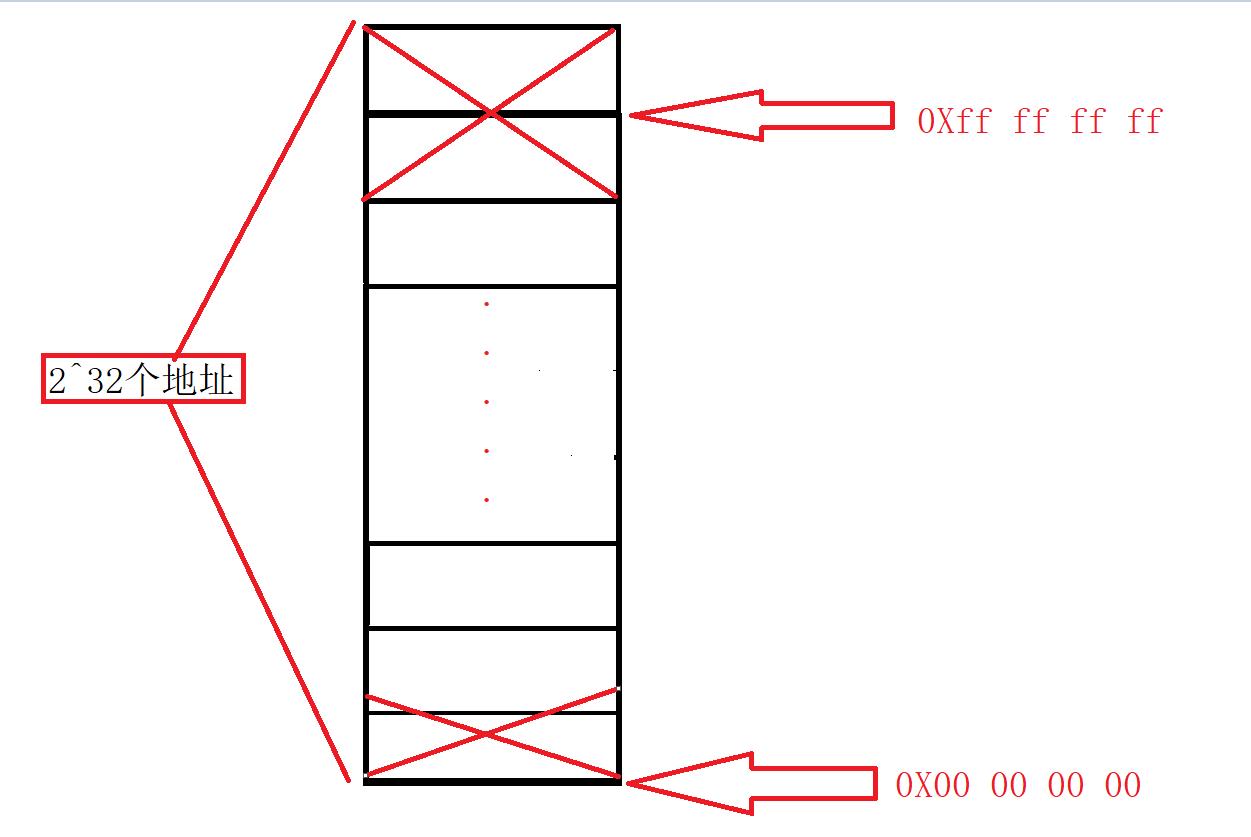
或者这样:
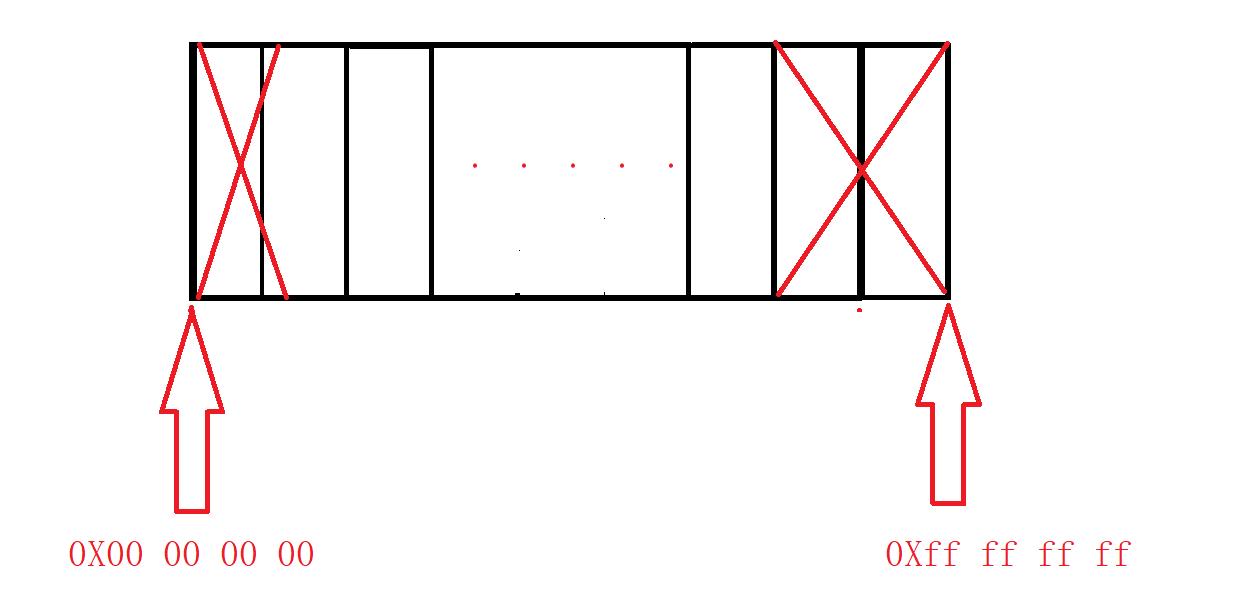
对于32位的操作系统来说,系统为我们分配了4G的内存大小,2^32次方就是4G,用二进制表示就是从全0加到全1的二进制的总和,而这些二进制在内存中的表现就是地址,地址用16进制数字表示就是从0X00 00 00 00到0Xff ff ff ff(用16进制表示地址是因为用2进制太复杂了,毕竟2进制有32个数字),知道了地址其实就是32个bit位组成,自然可以得到地址的大小就是4个字节,注意地址不过是内存单元的一个编号而已,代表了一个空间,每个内存单元能够容纳1个字节,例如要存放int的时候就需要4个内存单元。
在上面的图上我打上了两个×号,是为了表示其实我们能够使用的内存空间大小其实不足4G,在内存的高地址和低地址分别有一部分被系统本身占据,我们是不可以使用这部分的空间的。
C语言的数据分类
我们先要知道C语言的数据都有哪些种类:
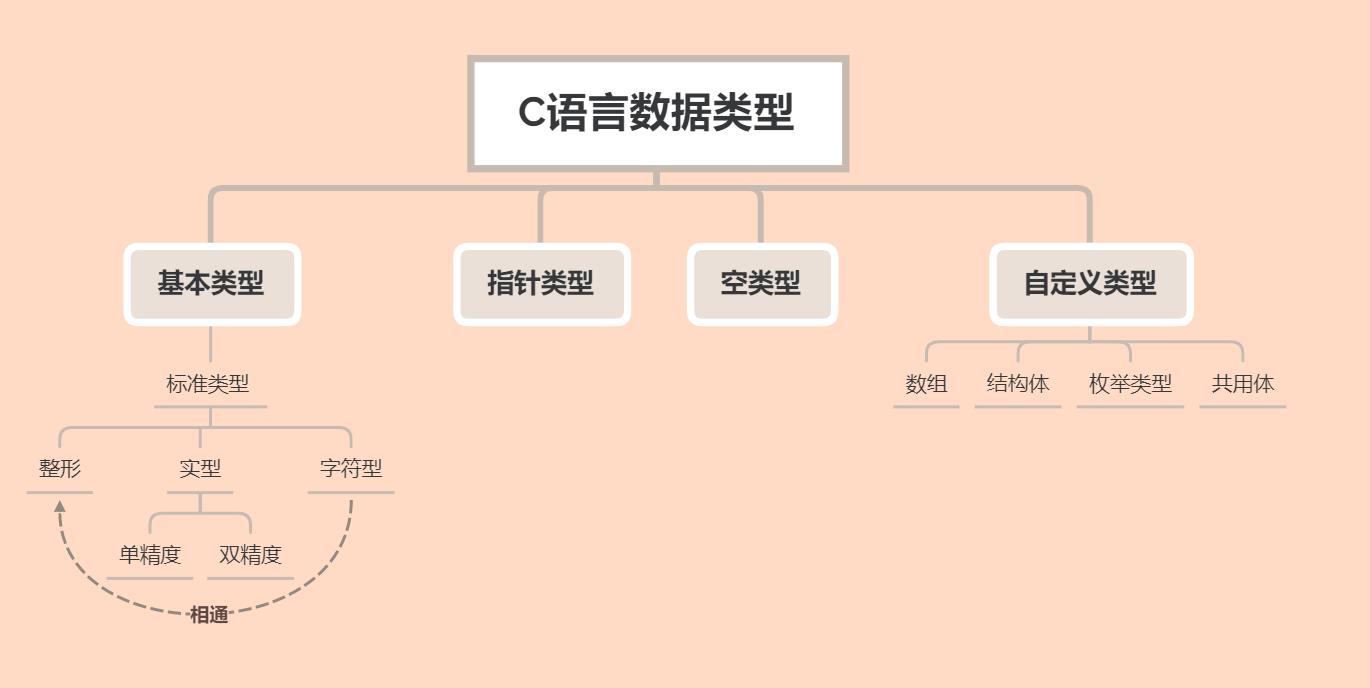
上面展示了C语言所涉及的所有数据类型。
整形在内存中的存储
整形有int,short int,long,long long,在这里以int为例来讲解整形在内存中的存储。
int是4个字节,内存为了存储int就要为其分配四个内存单元,而4这个字节用来存放什么呢?有基础的小伙伴肯定知道存放的是补码。
原码,反码,补码:
原码:直接将数字用二进制表示出来,有符号数的二进制的最高位为符号位,负数为1,正数为0。
反码:原码的符号位不变,其他位按位取反。
补码:反码加1即可。
接下来我们看一个例子。
int main()
{
int a = 10;
int b = -10;
return 0;
}
在这里我随便定义了两个变量a,b,我想通过先计算它们的补码,再通过调试获取它们在计算机中存储的信息来验证是否真的存放的是补码。
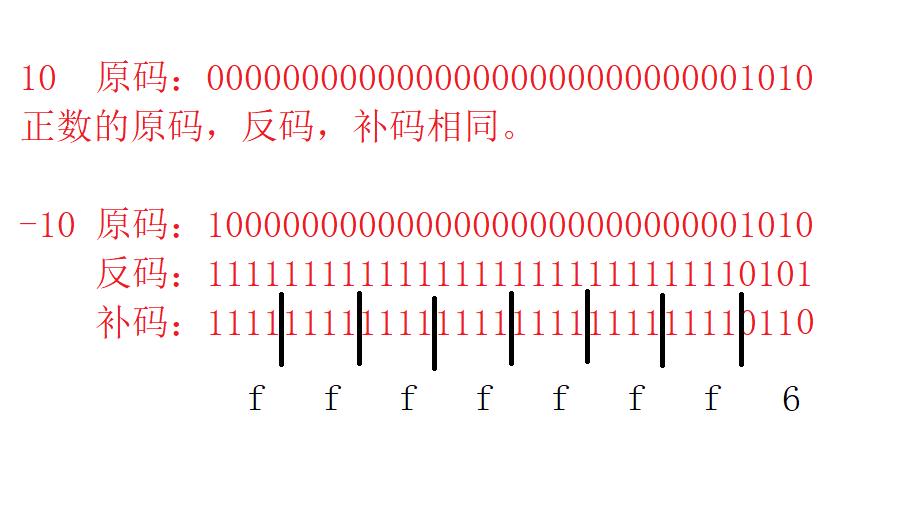
如果存放的是补码的话那么:
10在内存中应该是:0X00 00 00 0a,
-10在内存中应该是:0Xff ff ff f6。
调试打开内存后:
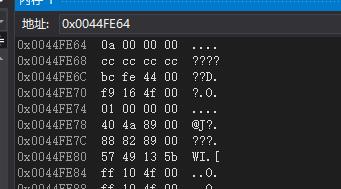
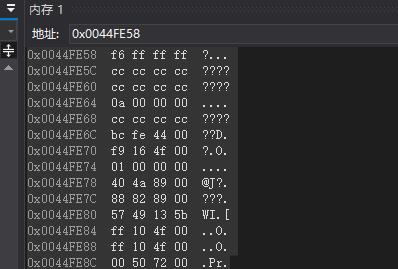
可以看出来确实存放的是补码,只不过这顺序怎么是反着的呢?
这就涉及到计算机对字节序的存储方式了。
大小端存储模式:
大端存储模式:将数据的低位保存在高地址处,高位保存在低地址处。
小端存储模式:将数据的地位保存在低地址处,高位保存在高地址处。
看了概念还是觉得模糊,不妨就按上面的例子做个例子:
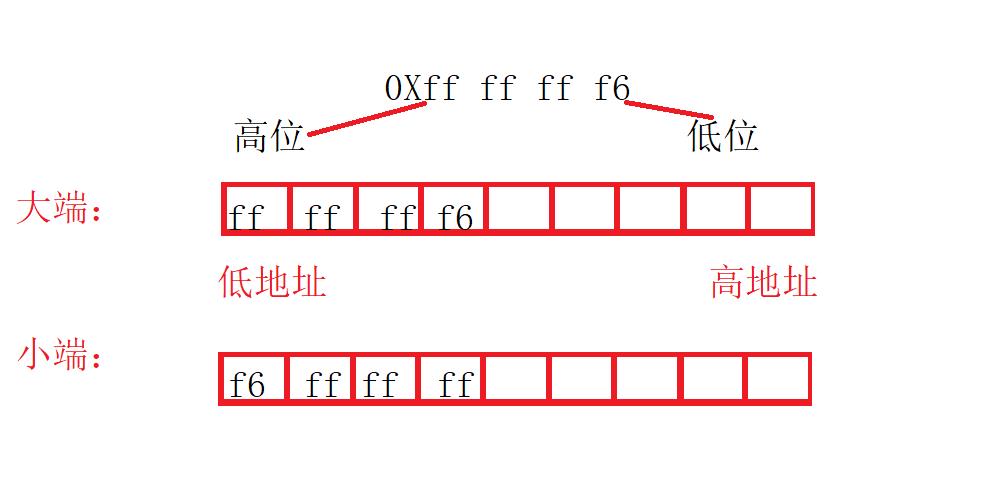
有了上面的这张图是不是就比较清晰了,对比内存图可以看到我的机器当前是按照小端存储进行的。
当然并不是所有的机器都是小端存储,那能不能写一个代码来显示机器到底是大端还是小端存储呢?
int main()
{
int a=1;
char *p=(char*)&a;
if(*p)
printf("小端\\n");
else
printf("大端\\n");
return 0;
}
为什么这段代码就可以判断大端小端呢?接下来就分析一下:

可以看到&a指向了1在内存中存储的第一个内存单元的地址处,这个内存单元中存放的分别是01和00,那如果我可以拿出01和00不就可以判断是大断还是小端了吗?01的话就是小端,00的话就是大端,那怎么样才能得到呢?
想要得到01和00,那就是指针解引用的时候访问一个字节的大小,我们知道指针的类型决定了指针解引用的时候可以向后访问几个字节的大小,但是&a得到的是int*类型的指针,解引用的时候会向后访问4个字节的大小,所以强制转换指针的类型,再将其赋值给p指针。
代码运行结果如下:
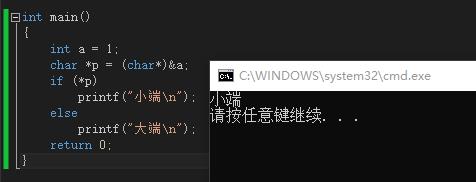
字符型数据的存储和整形是一样的,注意存的是它们的阿斯克码值。
浮点型在内存中的存储
再讲解浮点数的存储之前我们先看一个例子:
int main()
{
int n=9;
float*pfloat=(float*)&n;
printf("n的值为:%d\\n",n);
printf("*pfloat的值为:%f\\n",*pfloat);
*pfloat=9.0;
printf("num的值为:%d\\n",n);
printf("*pfloat的值为:%f\\n",*pfloat);
return 0;
}
读者可以先分析一下这个代码,看看结果和自己分析的有什么不一样的。
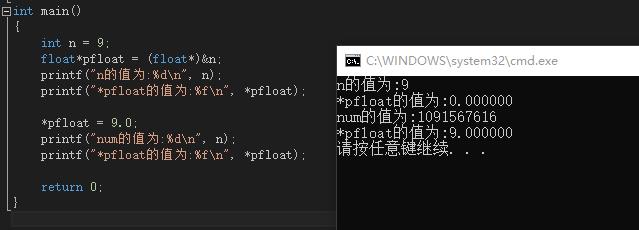
是不是发现结果有点出乎意料?一切都在于浮点数的存储方式。
博主自己对浮点数的理解如下:
将浮点数分为三部分,第一部分时指数,第二部分是符号位,第三部分是数字位。
例如:2.5
2.5用二进制表示为(注意不要和整数的补码混淆)10.01=1.01*2^1
2.5为正数,它的符号位就是0,指数为1,数字位为001(因为每个浮点数表示出来都是1.XXXX…,那干脆就不要1了,直接保留小数点后面的数字)
2.5这个浮点数被我们拆分完毕了,那么这三个部分在内存中到底该怎么存呢?
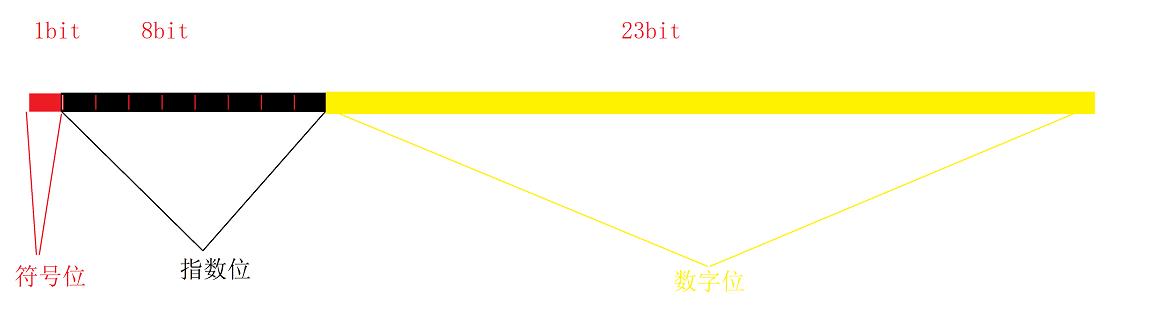
这张图很好的描述了3个部分分别是怎么存储到4个字节的内存空间中去的。
那么根据这张图我们可以推理出2.5在内存中存的是:
0 00000001 01000000000000000000000
那结果正确吗?调试得到:
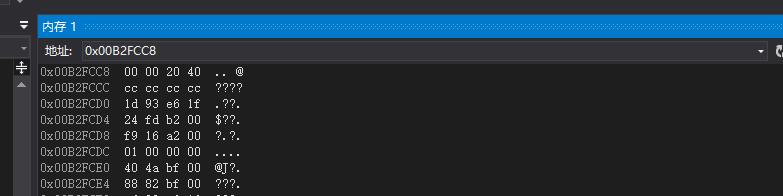
我们可以看到2.5在内存中存储的是00 00 20 40,将其转换为2进制就是:
0100 0000 0010 0000 0000 0000 0000 0000
这和我们得到的完全不一样啊,那说明我们的三个部分绝不是简单的直接存进去的。
对于符号位:和整数的符号位一样,正数为0,负数为1,没什么特殊的。
对于指数位:指数位是用来存放指数的,我们要明确指数位存放的是无符号整数,但是我们都知道指数是可以为负值的,那为了不与无符号整数冲突,我们给指数加上一个中间数来确保指数再0—255之间,这个中间数是127,我们将得到的数的二进制放进指数位中去。
当指数位全为0时:原浮点数的指数就是1-127(或者1-1023),数字位不在加上前面省略掉的1。
当指数位全为1时:如果数字位全为0,表示+/-无穷大。
对于数字位:将得到的数字放到数字位处,不够23个bit的时候后面补0。
有了上面的知识,让我们再尝试一次:
符号位就是0,没什么特殊的,指数位是1+127=128的二进制,就是10000000,数字位就是01000000000000000000000,将它们组合起来就是:
0 10000000 01000000000000000000000
转换为16进制就是 40 20 00 00和在内存中的一样,证明我们做对了。
读者有兴趣可以再次分析一遍刚开始的例子,相信有了上面的知识一定可以做出来。
数组在内存中的存储
“栈”是一种数据结构,数组便存储在栈上,在这里我们不用深入了解栈,只需要知道它是这样的:
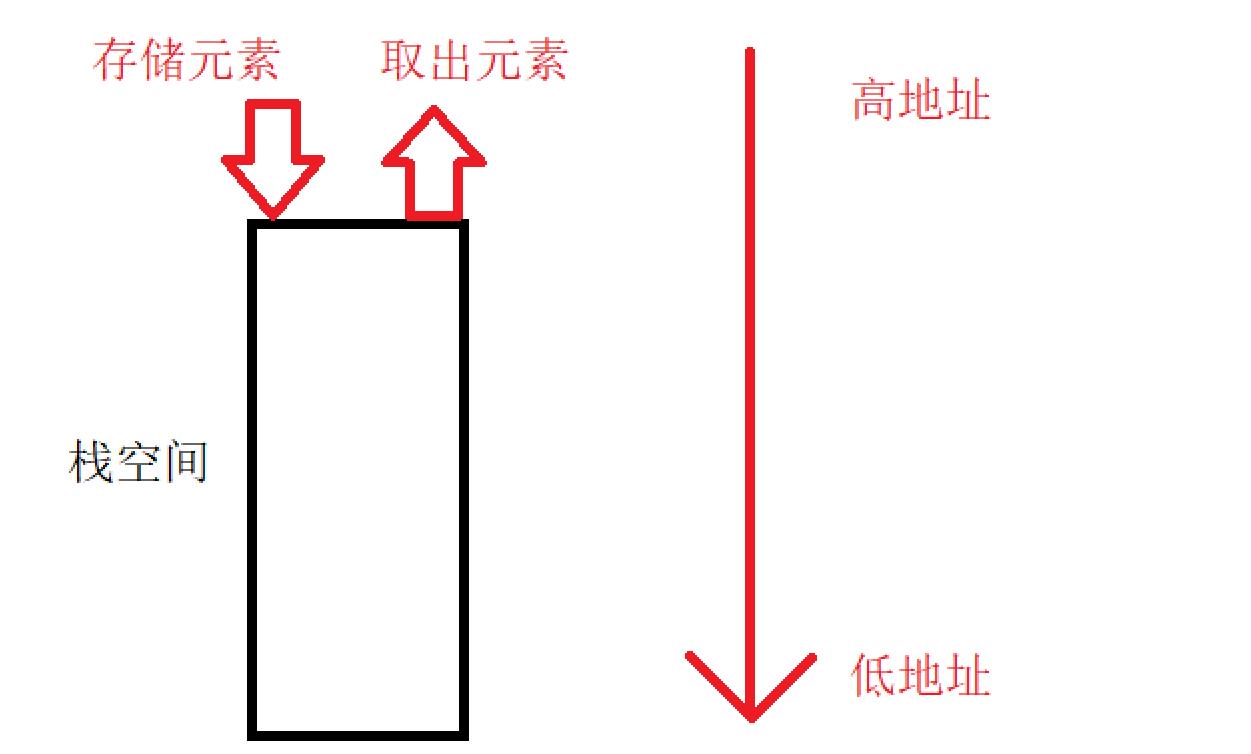
栈就像是“草履虫”,往栈空间放元素和读取元素都是从一个口进行的,在栈空间上存储元素是先使用高地址,后使用低地址的。
那么数组的存储就比较简单了:
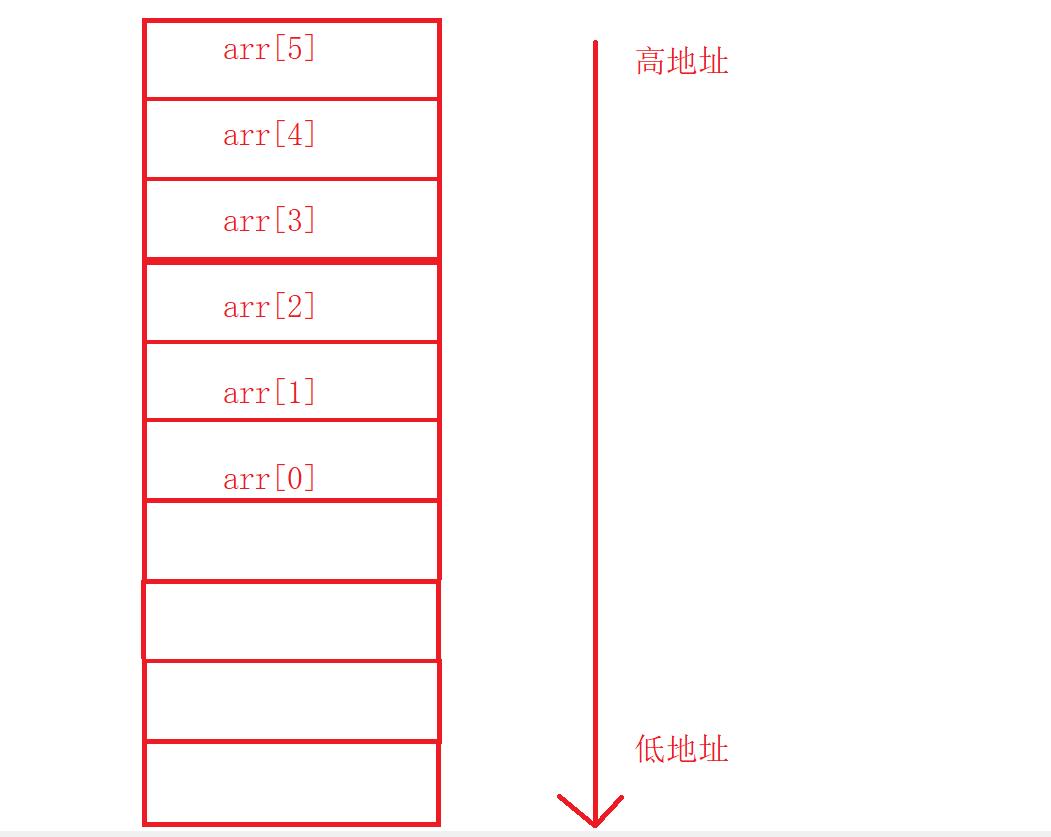
在上面定义了一个arr[6],可以看到它在栈上的存储方式。
这篇博客主要是带大家了解浮点型的存储方式,在非计算机专业老师基本不讲,所以我觉得有必要写一篇博客,至于结构体,联合体…会在后面的博客中和大家分享,如果您觉得博主写的还不错的话就三连支持一下吧,谢谢。
坚持学习,向大厂前进!!!
以上是关于看了这篇博客,再也不害怕别人问我把不把握得住数据存储了(初)的主要内容,如果未能解决你的问题,请参考以下文章