搞定kmp算法

Posted 2021-07-19 我是晓伍

系列文章目录

文章目录

• 系列文章目录
• 介绍
• 实现
• • 一.思路部分
  • 二.next数组的推导
  • 三.匹配过程
  • 三.代码实现
• 总结

---

介绍

在计算机科学中，Knuth-Morris-Pratt字符串查找算法（简称为KMP算法）可在一个字符串S内查找一个词W的出现位置。一个词在不匹配时本身就包含足够的信息来确定下一个匹配可能的开始位置，此算法利用这一特性以避免重新检查先前匹配的字符。

以上都是屁话，在c语言中，实现此功能的库函数叫做strstr，它被放在了string.h头文件中，这个函数的功能，用白话说就是给定一个主字符串和副字符串，之后再主字符串中找到副字符串，但是c中的这个函数用的是暴力匹配的算法，时间复杂度比较高。
例如：
字符串s = abcdefgg;
字符串t = cdef;

多余的不赘述，我们直接去实现kmp算法。

实现

一.思路部分

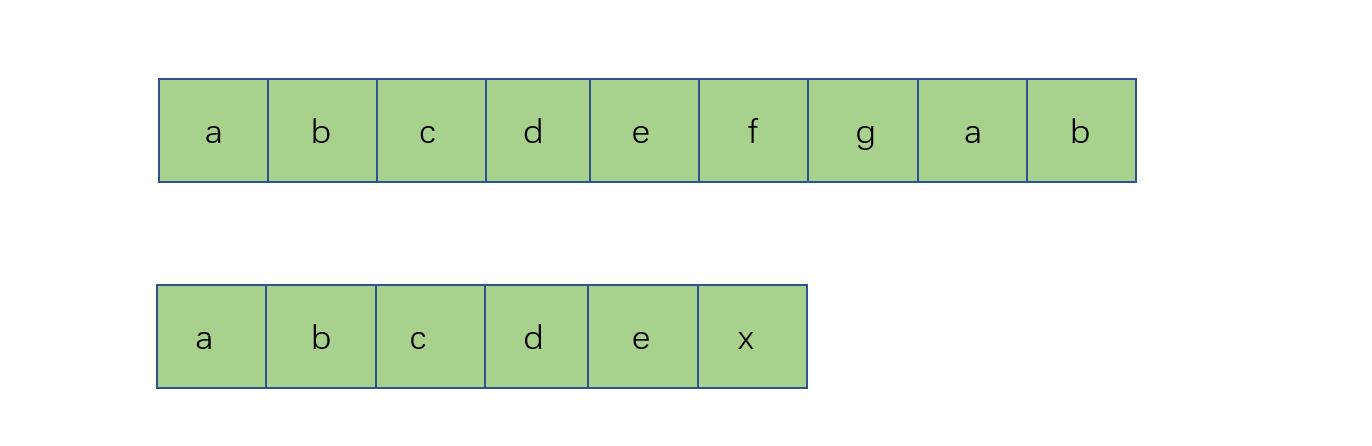
首先我们给出以下两个字符串s和t如图所示:

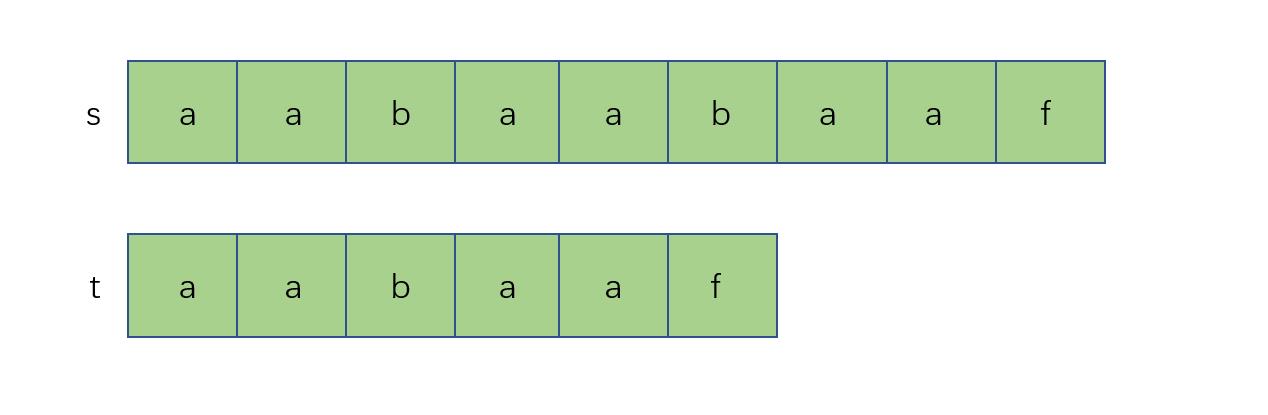
一开始的匹配过程很简单，如下图所示：

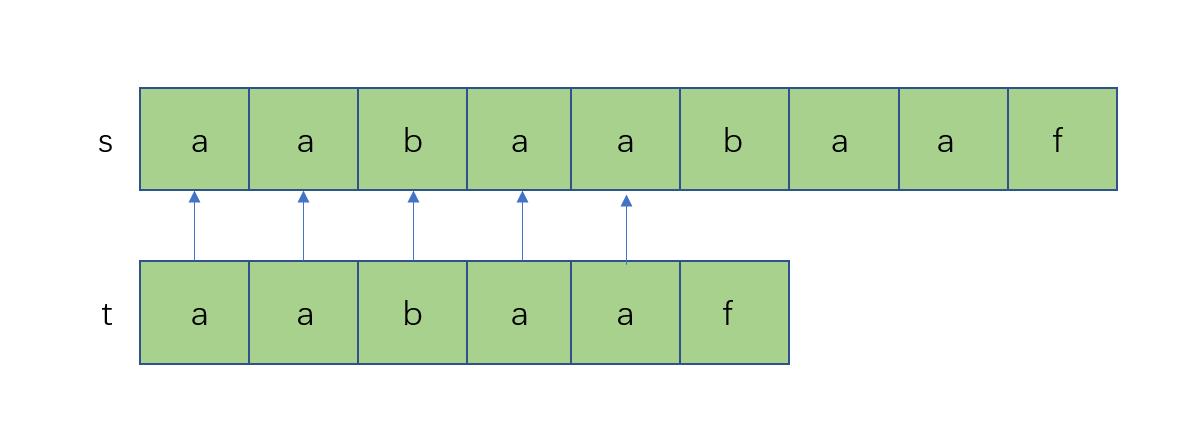
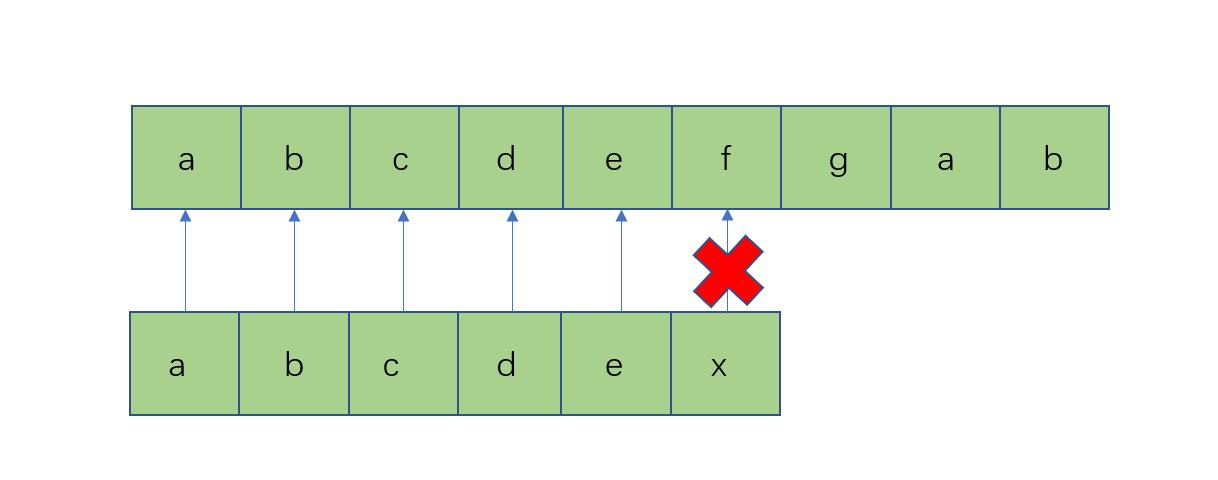
直到这里，下一位就开始出现匹配失败

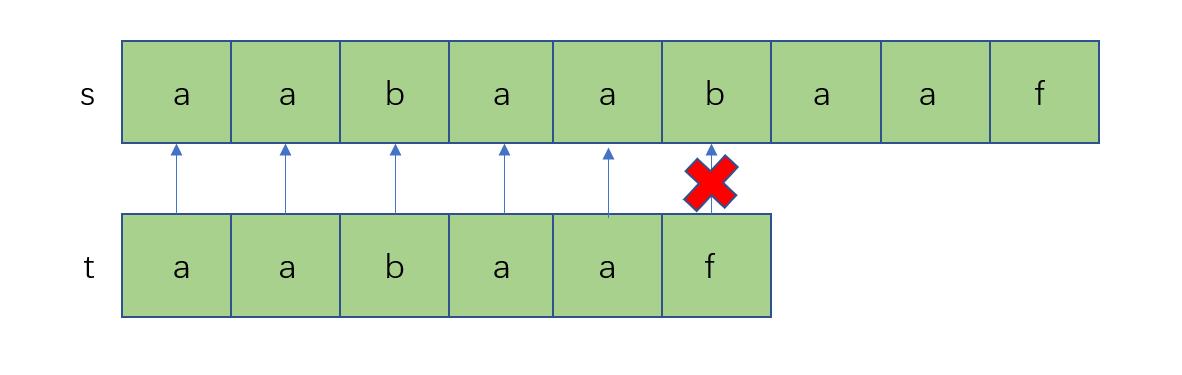
如果是按照传统的朴素匹配算法，这时候我们要从s的第二位和t的第一位开始匹配

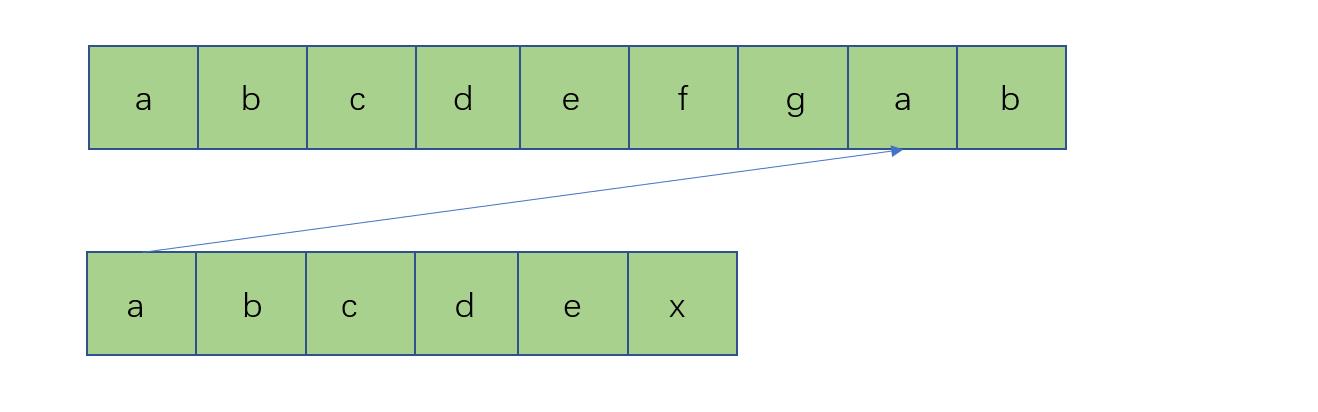
但是kmp的精妙之处就是它这时候会直接跳到如图所示的地方，之后b和b去做判断：

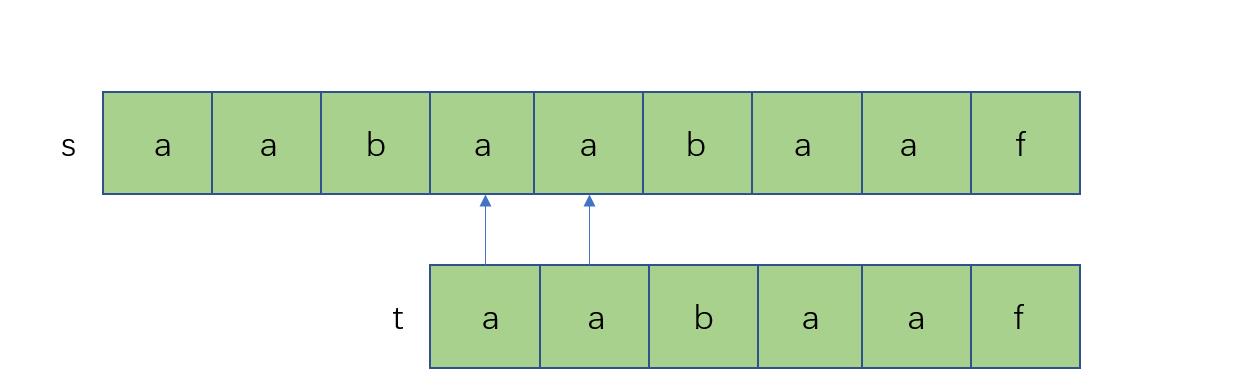
现在，我们来思考为啥会直接跳转，
我们再给两个这样的字符串

还是依旧正常匹配

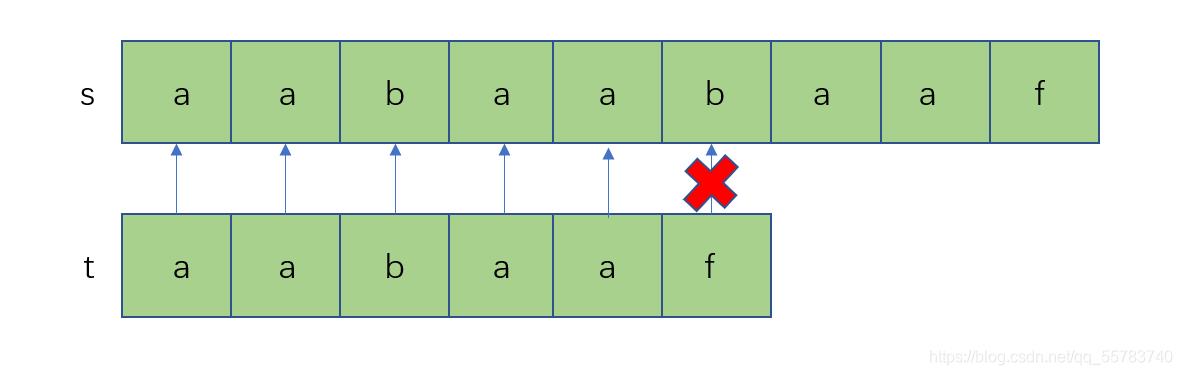
假设依旧按照朴素匹配，接下来上面的字符串从b开始与下面字符串的a匹配，不匹配，那上面的c与下面的a匹配，又不匹配，一直到上面字符串的第二个a与下面字符串第一个字符a才继续匹配上

现在我们来思考，从上面字符串的b开始与下面字符串a开始一直匹配失败的过程，这是不是可以省略一部分，因为在之前a=a,b=b,c=c…到x与f的匹配失败的时候，b到e都是匹配上的，而b与e又不和a相等，所以我们可以很硬气的说a无需和b与b到e匹配，直接去匹配e后面的f，这样就可以省略好多步骤

回到最初的一组字符串

当b与f不匹配时，这时候发现f前面的后缀aa与前缀aa是相同的，而b与b匹配好了，b又不和a相等，我们无需再用a去匹配b，那我们可以直接把副串前缀的aa移到后缀的位置上，然后从副串的b开始匹配

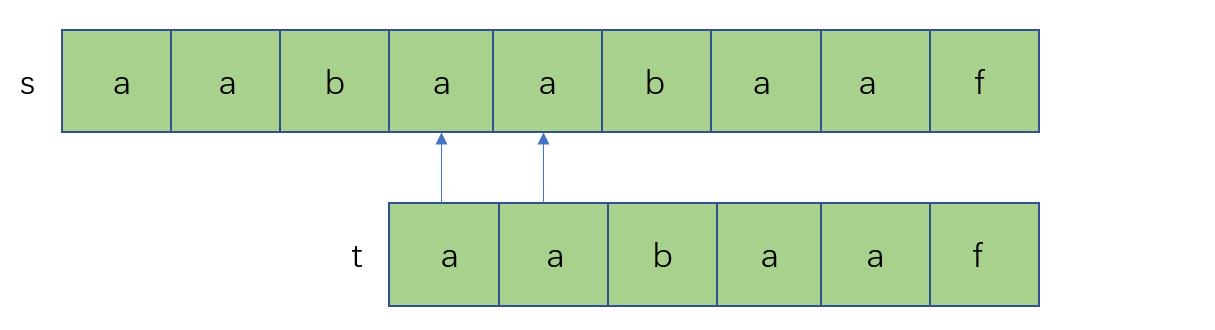
根据上面说的，我们大概知道，哦，这匹配机制和相等前后缀有关，因为后缀已经匹配过了，那把前缀怼过去，从前缀后面一位开始匹配就好了。

至此，我们准备工作做的差不多了，现在我们的目的是在匹配发生之前，对副串每个字符进行分析，分析到某个字符以后，这个字符前面的字符串的最长相等前后缀，嗯，俗话说，磨刀不误砍柴工，就是这样。

我们把副串第一个各个位置的相等前后缀数定义为数组next。

二.next数组的推导

首先我先给一个例子分析，之后再说推导过程

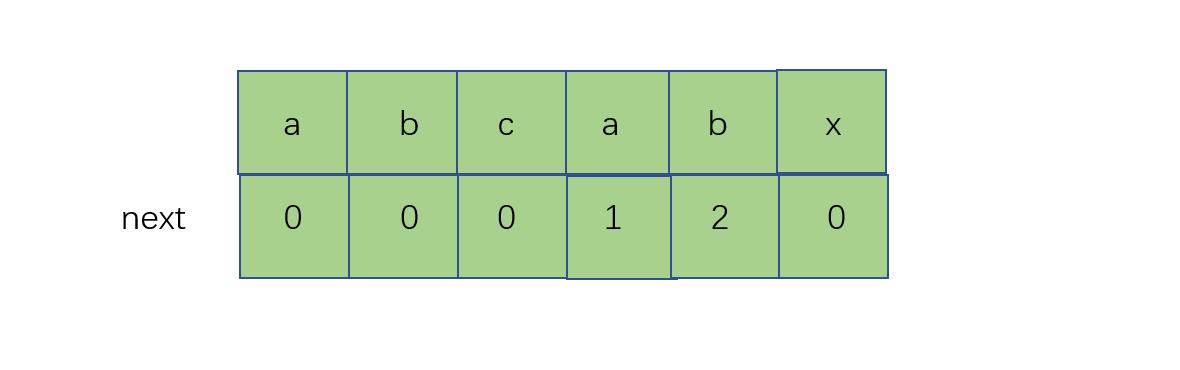
第二个a下的1代表着从头到此字符的字符串，最长相等前后缀的长度为1，类似的，第二个b下的2代表着从头到此字符的字符串(abcab)，最长的相等的前后缀长度为2，假设现在，x处匹配失败了,我们就看x前的字符串最长相等前后缀，假设x在T[j]处，那现在需要查找next[j-1]的值，也就是2，然后让j回溯到next[j-1]处，
如下图所示

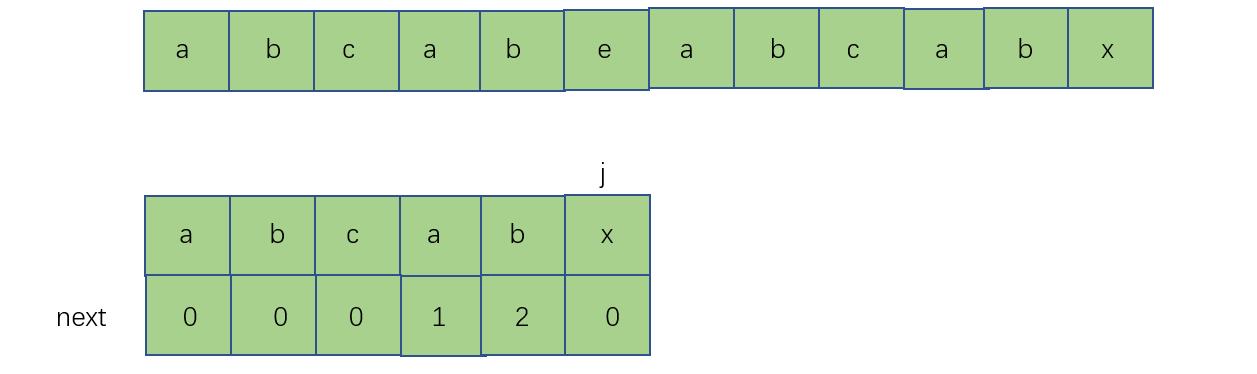
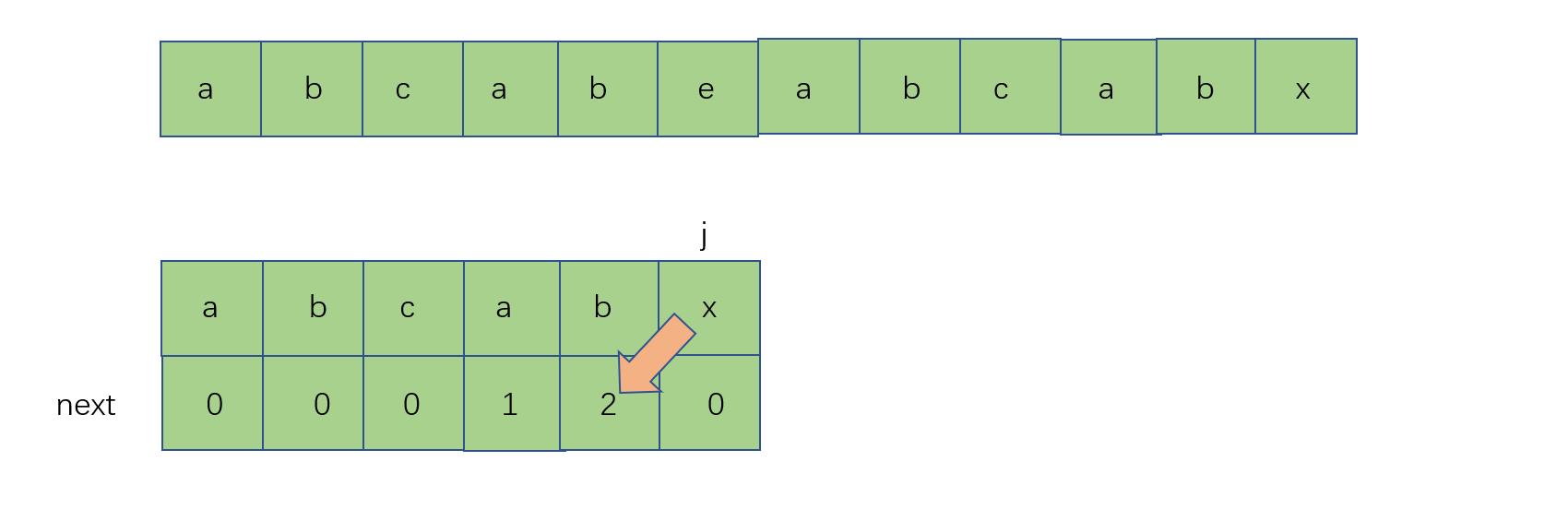
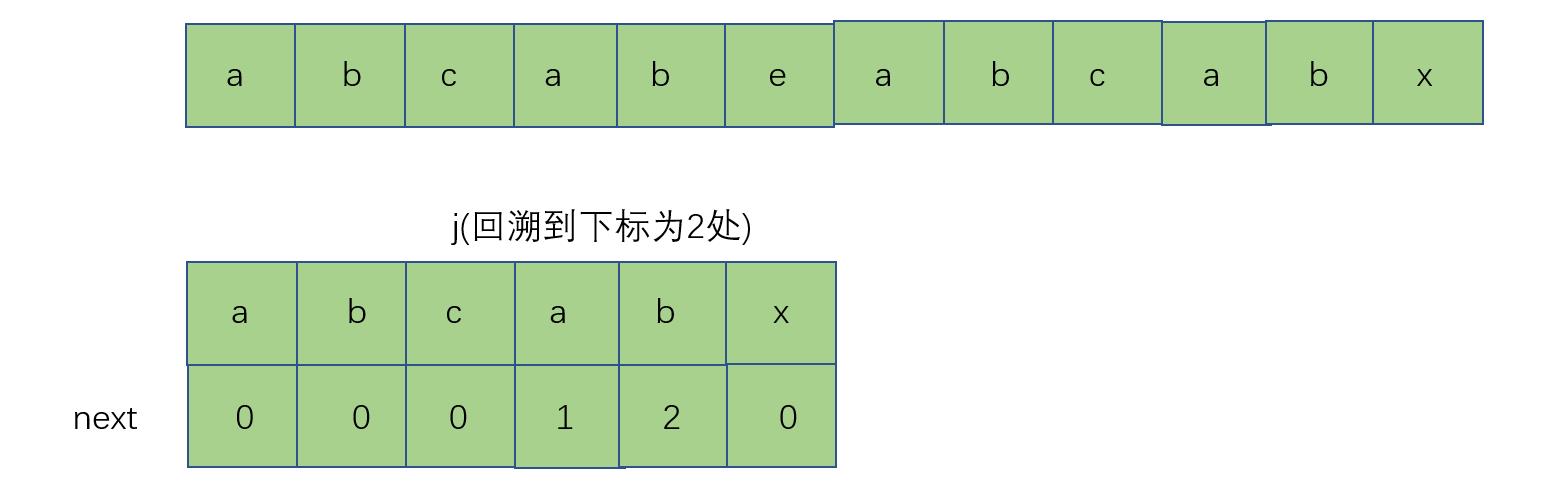
之后再与e重新匹配

首先，next[0]一定为0，因为只对应一个字符,之后我们这样

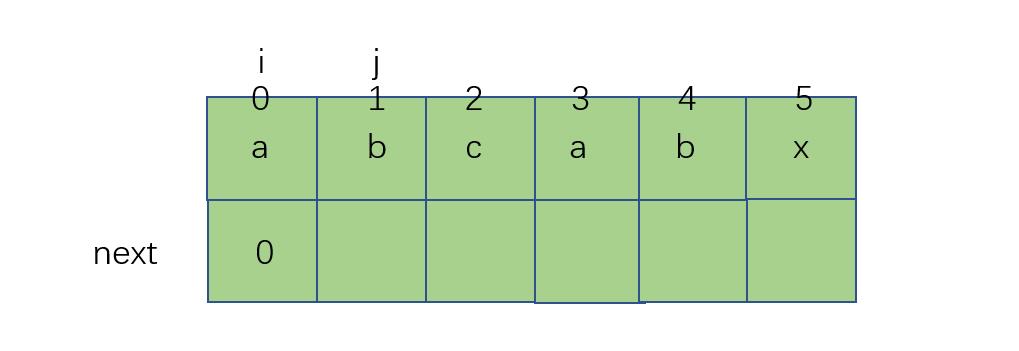
当i与j不匹配时，j++，之后让next[j-1] = 0,这样一直到如下图所示

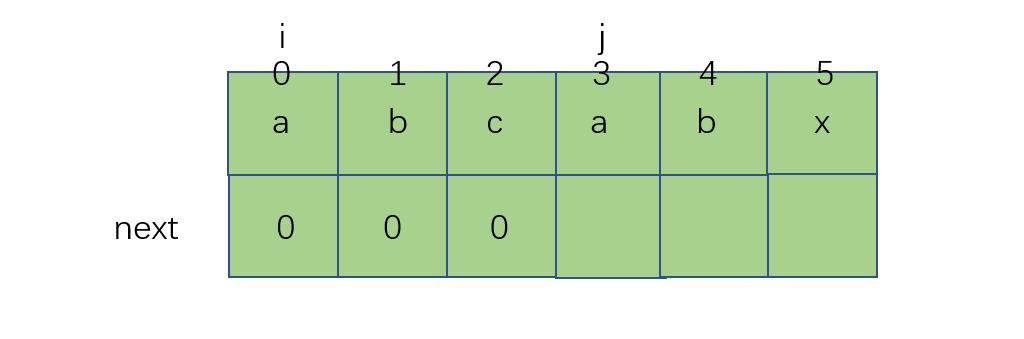
j处对应字符和i处相等了，说明了我们找到了公共的前后缀，这之后i++，j++，
next[j-1] = i。为什么i？因为i的值不仅代表着字符的位置，还代表着已经匹配的字符数，也就是相等前后缀数。
这样一直循环，我们就得到了next数组。

三.匹配过程

进过上面的描述，匹配过程已经比较简单了，回到第一组字符串s与t，给定两个指针ij分别指向字符串第一个字符

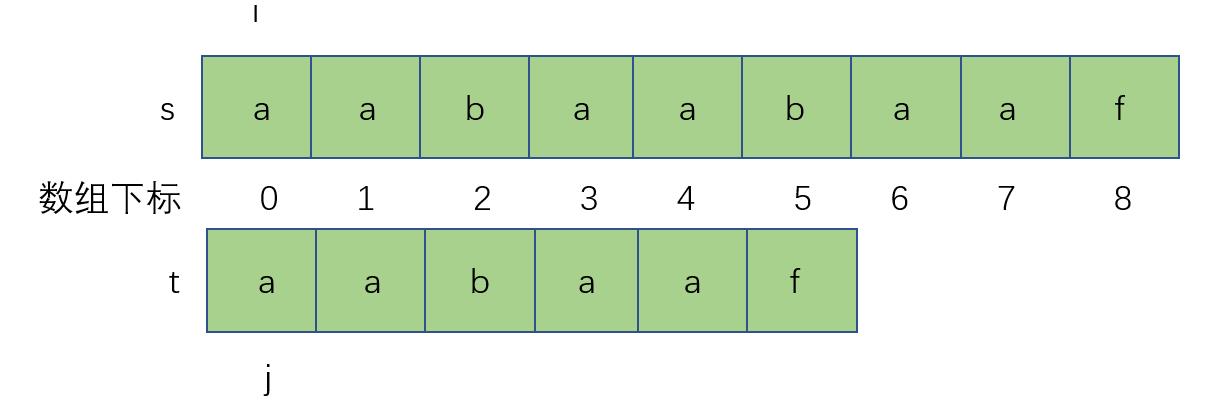
字符匹配成功，i++，j++，当匹配不成功时

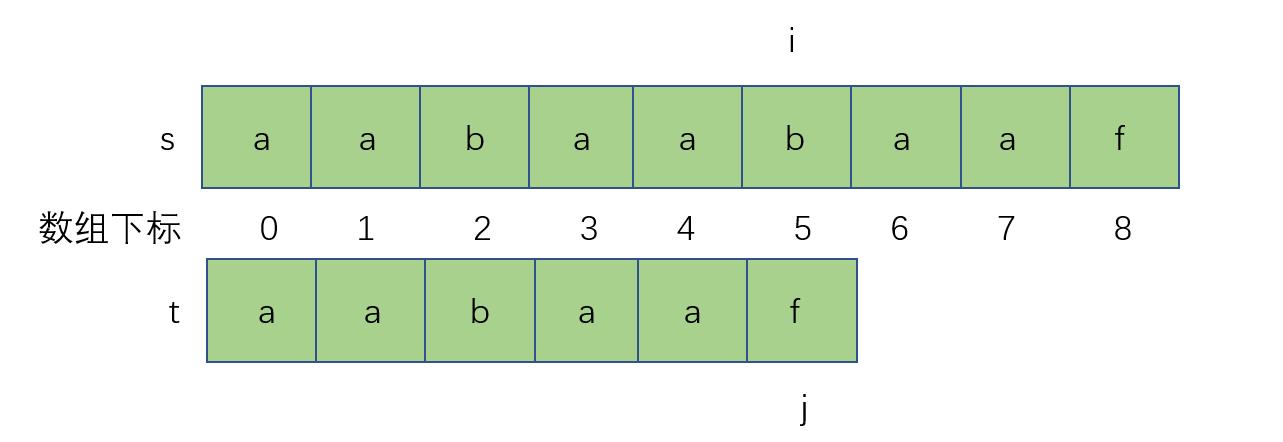
去查看next[j - 1]的值，该值代表着从0到j-1这个字符串的最大相等前后缀的长度,这之后让j跳转，因为数组下标从0开始,所以next[j - 1]的值刚好对应到j要跳转的值，也就是说，当匹配不成功时，j = next[j - 1]。

之后我们写出完整代码

三.代码实现

void getNext(char* s, int next[])
{
	assert(s != NULL);
	int i = 0;
	int j = 1;//用指针j去填充next
	next[0] = 0;//next的第一个元素一定是0
	int len = strlen(s);
	while (j < len)
	{
		//当i与j匹配上时，两个指针一起移动 next[j]的值来自i
		//因为i还承担着记录已有公共前后缀的作用
		//否则i需要通过前缀表回溯(前缀表用于记录相等前后缀)
		//这样可以直接把i定位到需要匹配的位置上
		if (s[i] == s[j])
		{
			i++;
			j++;
			next[j - 1] = i;
		}
		else
		{
			//分类讨论 - i等于0就不回溯了，否则造成死循环
			if (i == 0)
			{
				j++;
				next[j - 1] = 0;
			}
			else
			{
				i = next[i - 1];
			}
		}
	}
}

char* kmp(char* s, char* t)
{
	int i = 0;
	int j = 0;
	int Slen = strlen(s);
	int Tlen = strlen(t);
	int* next = (int*)malloc(Tlen * sizeof(int));//构造next数组
	getNext(t, next);//构造next数组
	while (i < Slen && j < Tlen)
	{
		//分类讨论，当匹配上时，i++，j++
		//匹配失败时，要考虑j是不是不能回溯了，如果不能回溯了i++
		//如果还能回溯，用next数组
		if (s[i] == t[j])
		{
			//匹配成功
			i++;
			j++;
		}
		else
		{
			//匹配不成功
			if (j == 0)
			{
				//j == 0时j不能再回溯，i++
				i++;
			}
			else
			{
				//j回溯到最大相等前缀的下一个元素处开始匹配
				j = next[j - 1];
			}
		}
	}
	if (j == Tlen)
	{
		return s + i - Tlen;
	}
	else
	{
		return NULL;
	}
}

总结

这个算法比较复杂，首先要理解算法原理，通过相等前后缀去匹配，之后推导next数组又是一个难点，但是，能把next数组推导出来，那这个算法也掌握的差不多了，如果喜欢的话，希望大家多多点赞！