chap2随机变量及其分布

Posted 2021-07-19 临风而眠

概率论与数理统计(2)：一维随机变量及其分布

文章目录

• 概率论与数理统计(2)：一维随机变量及其分布
• • 一.随机变量
  • • 1.定义
    • 2.分类
    • • ①离散型：只能取有限个值或可数个值
      • ②连续型：取得某一区间内的任何数值
  • 二.离散型随机变量
  • • 1.离散型随机变量的分布列
    • • 分布列也可以用表格形式直观表示：
      • 为什么叫分布列？
    • 2.常见离散型随机变量（Bernoulli distribution）
    • • ①两点分布（0-1分布/伯努利分布）
      • ②二项分布（Binomial distribution）
      • ③几何分布（Geometric distribution）
      • ④泊松分布
    • 3.随机变量的分布函数
    • • ①定义
      • ②性质
      • • (1)
        • (2)
        • (3)
        • (4)
    • 4.定义（离散型随机变量的分布函数）
  • 四.连续型随机变量
  • • 1.定义(连续型随机变量及其概率密度)
    • 2.常见的连续型随机变量
    • • ①均匀分布
      • ②指数分布
      • ③正态分布
      • • （1）定义
        • （2）正态分布函数
        • （3）图象
        • （4）正态分布与标准正态分布
        • • a.标准正态分布
          • b.转化为标准正态分布
  • 五.随机变量函数的分布
  • • 1.随机变量函数定义
    • 2.离散型随机变量函数的分布
    • 3.连续型随机变量函数的分布
    • • ①严格单调的连续型随机变量函数的分布
      • ②分段单调的连续型随机变量函数的分布
      • ①严格单调的连续型随机变量函数的分布
      • ②分段单调的连续型随机变量函数的分布

一.随机变量

1.定义

​ 设S是某随机试验的样本空间，如果对于每个e∈S，都有一个实数X(e)与其对应，则称X=X(e)为随机变量

​ (X=X(e)是定义在样本空间S上的实值单值函数)

​ 注：随机变量用大写字母X,Y,Z表示

2.分类

①离散型：只能取有限个值或可数个值

[eg]检验商品，抽取到的次品数

②连续型：取得某一区间内的任何数值

[eg]电视机寿命

二.离散型随机变量

1.离散型随机变量的分布列

​ 设离散型随机变量$X$所有可能取值为$x_k(k=1,2,...),X$取各个可能值的概率，即事件 { x = x k } \\{x=x_k\\} {x=xk​}的概率，为 P { X = x k } = p k , k = 1 , 2... ( ∗ ) P\\{X=x_k\\}=p_k,k=1,2...\\qquad(*) P{X=xk​}=pk​,k=1,2...(∗)

$(\ast )$式就是离散型随机变量$X$的分布列

​ 由概率的定义，$p_k$满足：$(1)p_k\ge 0(2){\sum }_k{p}_k=1$

分布列也可以用表格形式直观表示：

X	x1	x2	…	xn	…
P	p1	p2	…	pn	…

为什么叫分布列？

​ X的各个取值各占一些概率，这些概率合起来是1， 概率1以一定的规律分布在各个可能的值上

2.常见离散型随机变量（Bernoulli distribution）

①两点分布（0-1分布/伯努利分布）

​ 设离散型随机变量$X$只可能取0与1两个值，它的分布律为： P { X = k } = p k ( 1 − p ) 1 − k , k = 0 , 1 ( 0 < p < 1 ) P\\{X=k\\}=p^k(1-p)^{1-k},k=0,1\\quad(0<p<1) P{X=k}=pk(1−p)1−k,k=0,1(0<p<1)

表格形式：

X	0	1
P	1-p	p

注：记为
$$X\sim (0-1)，或X\sim B(1,p)$$

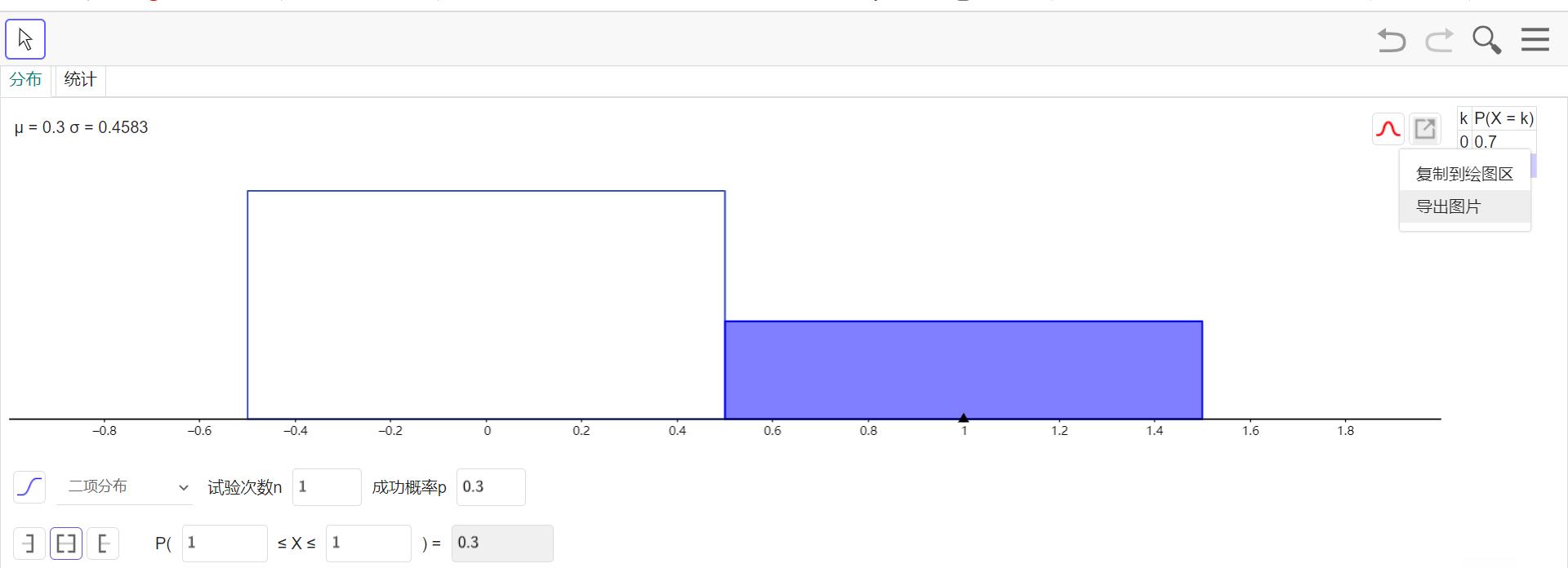
②二项分布（Binomial distribution）

​

​ 若以X表示n重贝努力试验中事件A发生的次数，X是一个随机变量，有分布列：
P { X = k } = C n k p k q n − k , 0 < p < 1 , q = 1 − p , k = 0 , 1 , . . . , n P\\left\\{X=k \\right\\}=C_n^kp^kq^{n-k},\\qquad0<p<1,\\quad q=1-p\\quad,k=0,1,...,n P{X=k}=Cnk​pkqn−k,0<p<1,q=1−p,k=0,1,...,n
称X服从参数为n,p的二项分布，X~B(n,p)

​

​ 各次试验是相互独立的，事件$A$在指定的$k(0⩽k⩽n)$次试验中发生，在其他$n-k$次试验中$A$不发生，这种指定方式有$\left(\genfrac{}{}{0ex}{}{n}{k}\right)$种，显然(1) P { X = k } ⩾ 0 , k = 0 , 1 , 2 , . . . , n P\\{X=k\\}\\geqslant 0,k=0,1,2,...,n P{X=k}⩾0,k=0,1,2,...,n ; (2) ∑ k = 0 n P { X = k } = ∑ k = 0 n ( n k ) p k q n − k = ( p + q ) n = 1 \\sum\\limits_{k=0}^nP\\{X=k\\}=\\sum\\limits_{k=0}^n{n\\choose k}p^kq^{n-k}=(p+q)^n=1 k=0∑n​P{X=k}=k=0∑n​(kn​)pkqn−k=(p+q)n=1

​ 当n=1时，二项分布就是（0-1）分布

概率质量函数图象：

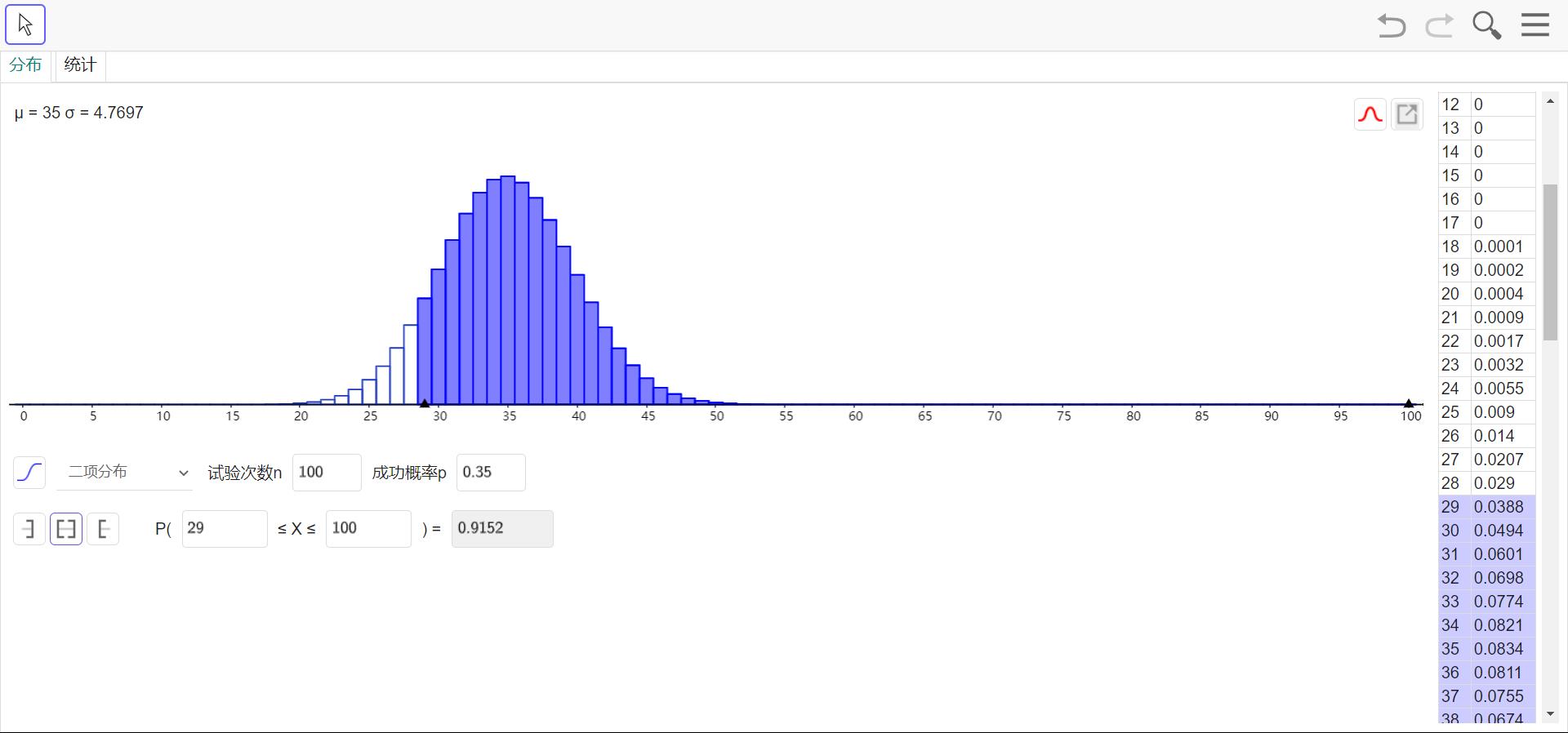
概率分布函数

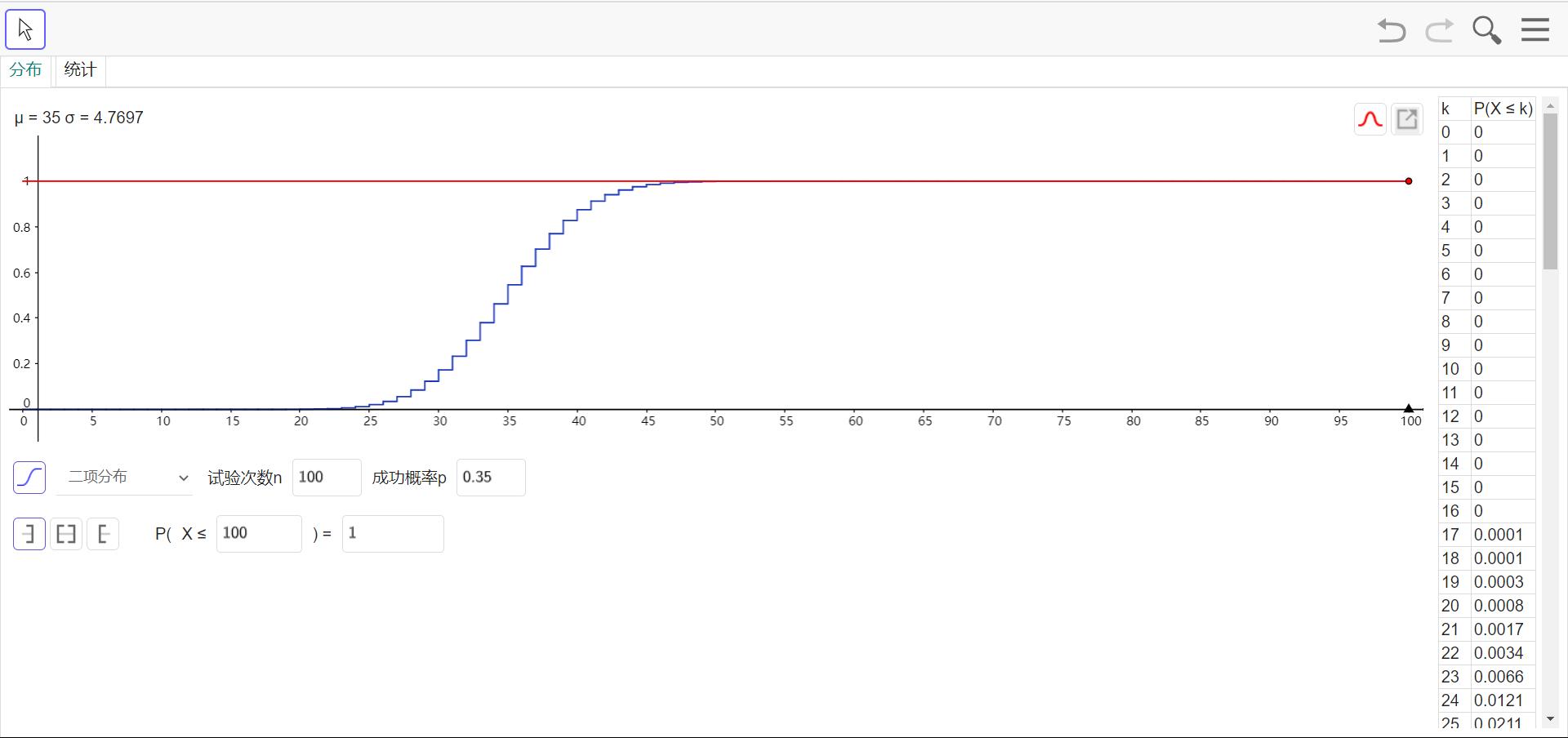
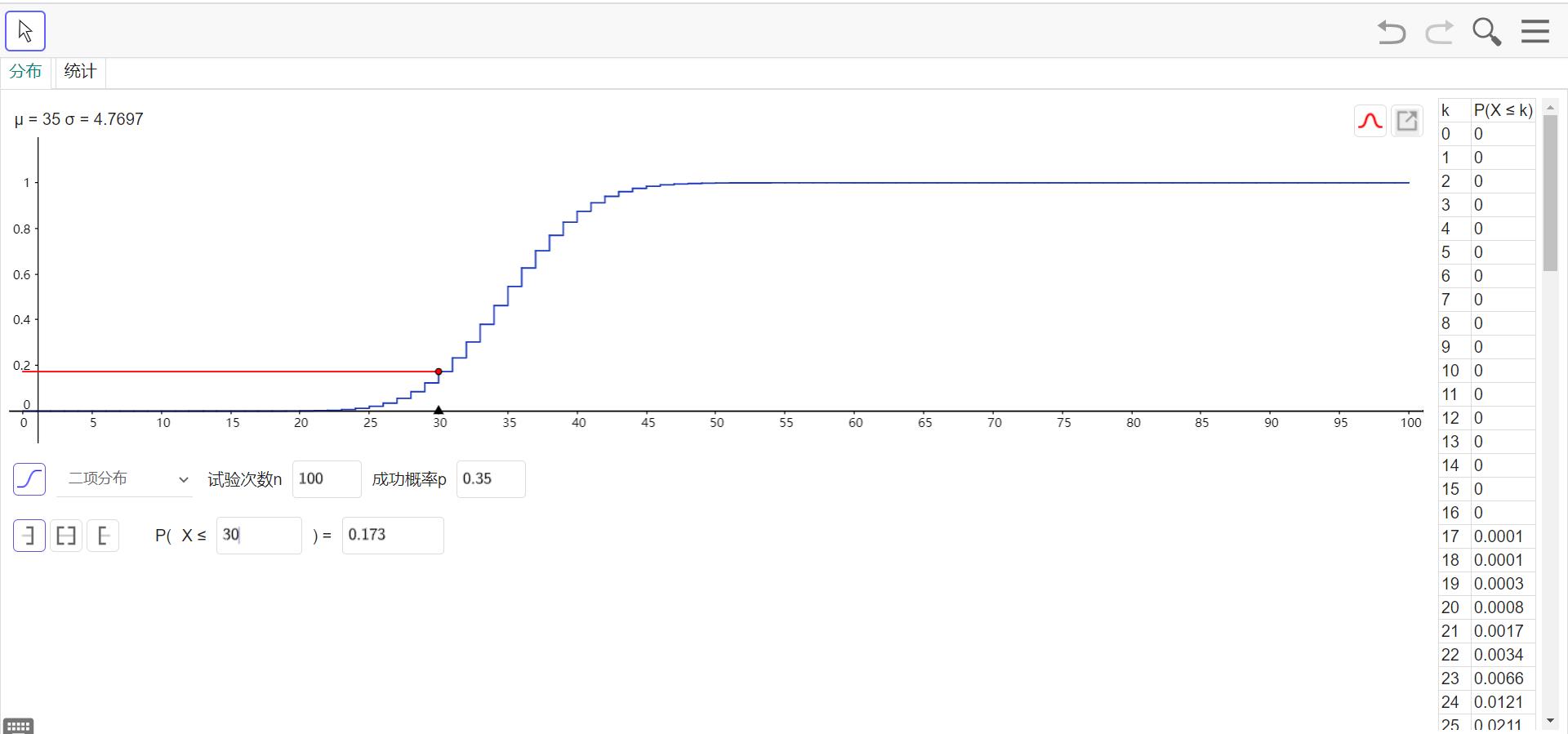
此处强烈安利Geogebra在线版（下载下来我发现反而运行速度没有那么快）,直通Geogebra概率统计计算器（上图所示）点击这里

我比较喜欢折腾，又去学着用python画了一下二项分布的概率质量函数

(概率质量函数是离散随机变量在各特定取值上的概率。概率质量函数和概率密度函数概率密度函数不同之处在于：概率质量函数是对离散随机变量定义的，本身代表该值的概率；概率密度函数是对连续随机变量连续随机变量定义的，本身不是概率，只有对连续随机变量的概率密度函数在某区间内进行积分后才是概率。)

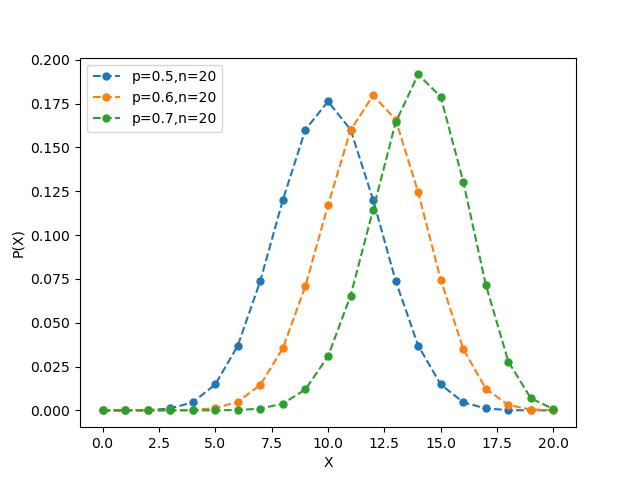
代码如下：

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
Ps = [0.5, 0.6, 0.7]
Ns = [20, 20, 20]
colors = ['blue', 'green', 'red']
for p,n, c in zip(Ps, Ns, colors):

    binomDist = stats.binom(n, p)
    P_k = binomDist.pmf(np.arange(n + 1))
    #概率质量函数（probability mass function，简写为pmf）
	label='p={},n={}'.format(p, n)
    plt.plot(P_k, '--',marker='o', label=label, ms=5)
    plt.xlabel('X')
    plt.ylabel('P(X)')
    plt.legend()
    plt.show()
    

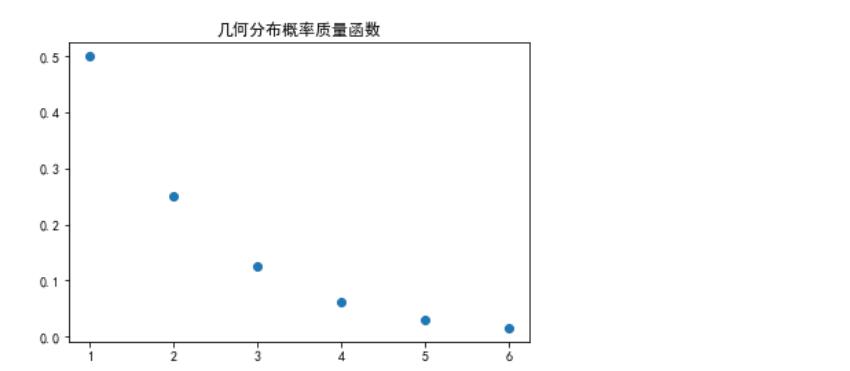
③几何分布（Geometric distribution）

​ 在重复独立试验中，事件A发生的概率为p，设X为直到A发生为止所进行的试验次数，则X的分布列为
P { X = k } = q k − 1 p , k = 1 , 2 , . . . P\\left\\{X=k\\right\\}=q^{k-1}p,\\qquad k=1,2,... P{X=k}=qk−1p,k=1,2,...
则称X服从参数为p的几何分布，$X\sim G(p)$

​

④泊松分布

​ 若随机变量X的分布列为
P { X = k } = λ k k ! e − λ , k = 0 , 1... P\\left\\{X=k\\right\\}=\\frac{\\lambda^k}{k!}e^{-\\lambda},\\qquad k=0,1... P{X=k}=k!λk​e−λ,k=0,1...
则称X服从参数为λ的泊松分布，X~P(λ)

​

​ 泊松分布可作为二项分布的极限而得到。一般的说，若$X\sim B(n,p)$,其中n很大，p很小，因而 n p = λ np=\\lambda 二维随机变量及其分布

机器学习基础知识之概率论的多维随机变量及其分布

机器学习基础知识之概率论的随机变量及其分布

机器学习基础知识之概率论的随机变量及其分布

概率论与数理统计：一维随机变量及其分布

概率论与数理统计:二维随机变量及其分布