微积分——曲线积分
Posted 临风而眠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了微积分——曲线积分相关的知识,希望对你有一定的参考价值。
曲线积分
文章目录
一.第一型曲线积分
是对弧长的曲线积分
1.性质
①线性性质
∫ L [ f ( x , y ) ± g ( x , y ) ] d s = ∫ L f ( x , y ) d x ± ∫ L g ( x , y ) d s ∫ L k f ( x , y ) d s = k ∫ L f ( x , y ) d s ( k 为 常 数 ) \\int_L[f(x,y)\\pm g(x,y)]ds=\\int_Lf(x,y)dx\\pm \\int_Lg(x,y)ds \\\\ \\int_Lkf(x,y)ds=k\\int_Lf(x,y)ds\\qquad (k为常数) ∫L[f(x,y)±g(x,y)]ds=∫Lf(x,y)dx±∫Lg(x,y)ds∫Lkf(x,y)ds=k∫Lf(x,y)ds(k为常数)
(本质是极限,体现了极限的线性性质)
②
若在L上有
f
(
x
,
y
)
⩽
g
(
x
,
y
)
f(x,y)\\leqslant g(x,y)
f(x,y)⩽g(x,y)成立,则
∫
L
f
(
x
,
y
)
d
s
⩽
∫
L
g
(
x
,
y
)
d
s
\\int_Lf(x,y)ds\\leqslant \\int_Lg(x,y)ds
∫Lf(x,y)ds⩽∫Lg(x,y)ds
③
∣ ∫ L f ( x , y ) d s ∣ ⩽ ∫ L ∣ f ( x , y ) ∣ d s \\big|\\int_Lf(x,y)ds\\big|\\leqslant \\int_L\\big|f(x,y)\\big|ds ∣∣∫Lf(x,y)ds∣∣⩽∫L∣∣f(x,y)∣∣ds
④对称奇偶性
若曲线L关于x=0对称,而
L
+
=
{
(
x
,
y
)
∣
(
x
,
y
)
∈
L
,
x
⩾
0
}
,
L_+=\\{(x,y)|(x,y)\\in L,x\\geqslant 0\\},
L+={(x,y)∣(x,y)∈L,x⩾0},则
∫
L
f
(
x
,
y
)
d
s
=
{
0
,
当
f
(
−
x
,
y
)
=
−
f
(
x
,
y
)
时
2
∫
L
+
f
(
x
,
y
)
d
s
,
当
f
(
−
x
,
y
)
=
f
(
x
,
y
)
时
\\int_Lf(x,y)ds=\\left\\{ \\begin{array}{lr} 0 &,当f(-x,y)=-f(x,y)时\\\\ 2\\int_{L_+}f(x,y)ds &,当f(-x,y)=f(x,y)时 \\\\ \\end{array} \\right.
∫Lf(x,y)ds={02∫L+f(x,y)ds,当f(−x,y)=−f(x,y)时,当f(−x,y)=f(x,y)时
若曲线L关于y=0对称,而
L
+
=
{
(
x
,
y
)
∣
(
x
,
y
)
∈
L
,
y
⩾
0
}
,
L^+=\\{(x,y)|(x,y)\\in L,y\\geqslant 0\\},
L+={(x,y)∣(x,y)∈L,y⩾0},则
∫
L
f
(
x
,
y
)
d
s
=
{
0
,
当
f
(
x
,
−
y
)
=
−
f
(
x
,
y
)
时
2
∫
L
+
f
(
x
,
y
)
d
s
,
当
f
(
x
,
−
y
)
=
f
(
x
,
y
)
时
\\int_Lf(x,y)ds=\\left\\{ \\begin{array}{lr} 0 &,当f(x,-y)=-f(x,y)时\\\\ 2\\int_{L^+}f(x,y)ds &,当f(x,-y)=f(x,y)时 \\\\ \\end{array} \\right.
∫Lf(x,y)ds={02∫L+f(x,y)ds,当f(x,−y)=−f(x,y)时,当f(x,−y)=f(x,y)时
2.几何意义
∫ L 1 d s = L 的 长 度 \\int_L1ds=L的长度 ∫L1ds=L的长度
3.计算
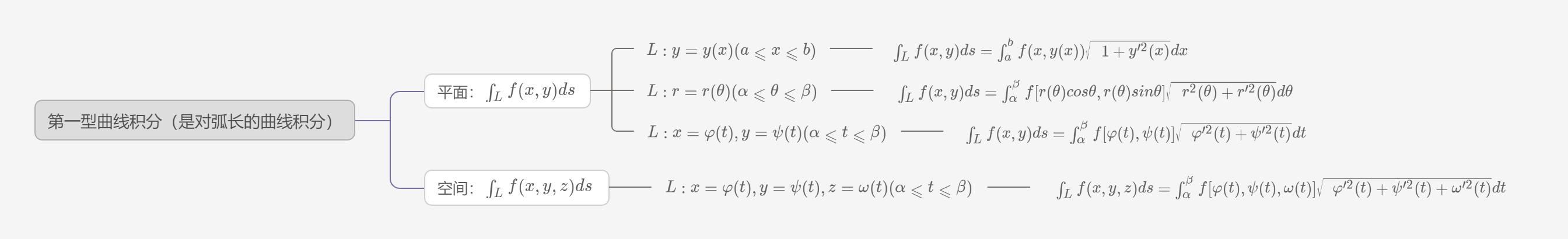
(上面的图是用Process On画的,强烈安利这个在线绘图工具,近期增加的Latex公式编辑功能,超级香!)
(上传图片是用的GitHub+PicGo图床,也超级香!)
注:
①最后都是转化为定积分计算,积分下限一定要小于积分上限
②
上图中给出的平面中第一型曲线积分第一种情况其实是参数方程的特殊情况,可以把 x x x当作参数, x = x , x ′ ( x ) = 1 x=x,x'(x)=1 x=x,x′(x)=1
若给出 x = g ( y ) , x=g(y), x=g(y),则可以把y选为变量
二.第二型曲线积分
是对坐标的曲线积分,要注意积分弧段的方向
1.基本概念
有界向量函数 F ⃗ ( x , y ) = ( P ( x , y ) , Q ( x , y ) ) \\vec F(x,y)=(P(x,y),Q(x,y)) F(x,y)=(P(x,y),Q(x,y))在 L L L上的第二型曲线积分为 ∫ L P ( x , y ) d x + Q ( x , y ) d y \\int_LP(x,y)dx+Q(x,y)dy ∫LP(x,y)dx+Q(x,y)dy,其中 P ( x , y ) , Q ( x , y ) P(x,y),Q(x,y) P(x,