微积分——微分方程
Posted 临风而眠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了微积分——微分方程相关的知识,希望对你有一定的参考价值。
常微分方程
文章目录
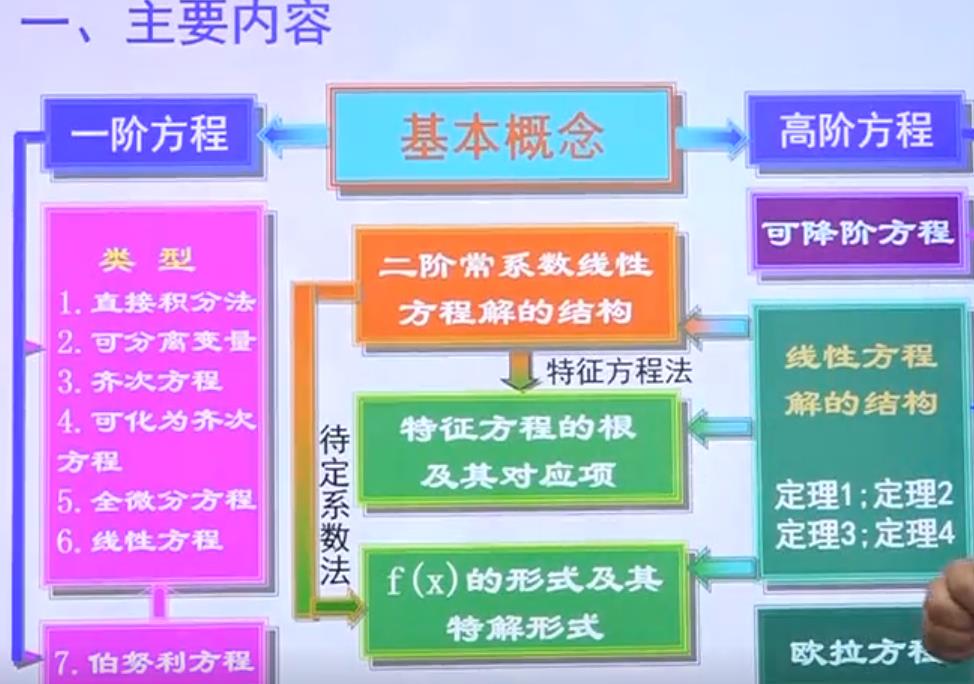
- 常微分方程
- 一.基本概念
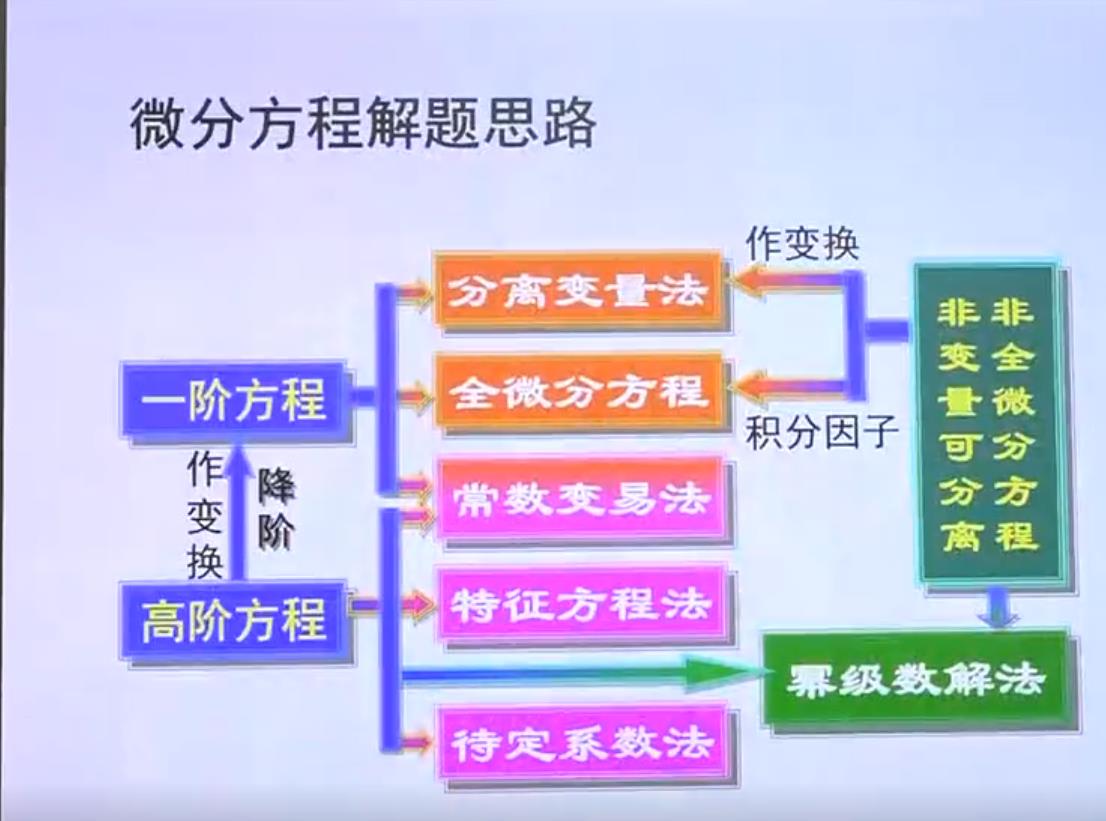
- 二.一阶微分方程
- 三.可积的高阶微分方程
- 四.线性微分方程及其通解结构
- 五.常系数齐次线性微分方程
- 六.常系数非齐次线性微分方程
- 1. y ′ ′ + p y ′ + q y = P m ( x ) e b x y''+py'+qy=P_m(x)e^{bx} y′′+py′+qy=Pm(x)ebx
- 2. y ( n ) + a 1 y ( n − 1 ) + a 2 y ( n − 2 ) + ⋯ + a n − 1 y ′ + a n y = e b x [ P m ( x ) cos ω x + P l ( x ) s i n ω x ] y^{(n)}+a_1y^{(n-1)}+a_2y^{(n-2)}+\\cdots+a_{n-1}y'+a_ny=e^{bx}[P_m(x)\\cos \\omega x+P_l(x)sin\\omega x] y(n)+a1y(n−1)+a2y(n−2)+⋯+an−1y′+any=ebx[Pm(x)cosωx+Pl(x)sinωx]
一.基本概念
1.微分方程定义
含有未知函数的导数或微分的,联系着自变量、未知函数及其导数或微分的方程叫做微分方程
(未知函数仅依赖于一个自变量的微分方程叫常微分方程,依赖于多个自变量的微分方程叫做偏微分方程,下仅讨论常微分方程)
如: d y d x = 1 x , x ′ + x = 0 , d 2 y d x 2 = 10 \\dfrac{dy}{dx}=\\dfrac{1}{x},x'+x=0,\\dfrac{d^2y}{dx^2}=10 dxdy=x1,x′+x=0,dx2d2y=10都是微分方程,而方程 x 2 + y 2 = 1 x^2+y^2=1 x2+y2=1不是微分方程,而是隐函数方程
2.微分方程的阶
微分方程的阶:在微分方程中出现的未知函数的导数的最高阶数,如
d
y
d
x
=
1
x
\\dfrac{dy}{dx}=\\dfrac{1}{x}
dxdy=x1是一阶的,
d
2
y
d
x
2
=
10
\\dfrac{d^2y}{dx^2}=10
dx2d2y=10是二阶的,
x
2
y
′
′
′
+
4
(
y
′
)
4
=
x
x^2y'''+4(y')^4=x
x2y′′′+4(y′)4=x是三阶的,n阶微分方程的一般形式为:
F
(
x
,
y
,
y
′
,
⋯
,
y
(
n
)
)
=
0
(
∗
)
F(x,y,y',\\cdots,y^{(n)})=0\\qquad (*)
F(x,y,y′,⋯,y(n))=0(∗)
微分方程是n阶,则式中
y
(
n
)
y^{(n)}
y(n)必须出现
上述形式为隐式方程,若能解出 y ( n ) = f ( x , y , y ′ , ⋯ , y ( n − 1 ) ) , y^{(n)}=f(x,y,y',\\cdots,y^{(n-1)}), y(n)=f(x,y,y′,⋯,y(n−1)),则为显式方程
用导数的阶定义方程的阶
不要混淆导数的阶数和导数的次方数
线性方程
若 ( ∗ ) (*) (∗)式中 y , y ′ , ⋯ , y ( n ) y,y',\\cdots,y^{(n)} y,y′,⋯,y(n)都是一次的(线性的),则称 ( ∗ ) (*) (∗)为线性方程
n阶线性方程的一般形式为: 以上是关于微积分——微分方程的主要内容,如果未能解决你的问题,请参考以下文章
f
(
x
)
=
y
(
n
)
+
p
1
(
x
)
y
(
n
−
1
)
+
p
2
(
x
)
y
(
n
−
2
)
+
⋯
+
p
n
−
1
(
x
)
y
′
+
p
n
(