2020年高数下期末B错题
Posted 九死九歌
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2020年高数下期末B错题相关的知识,希望对你有一定的参考价值。
写完A卷系统地复习了一下高数,做起来还是挺轻松的,整份卷子因为知识性错误错了俩题丢了几分,但是感觉自己啥都会就狂了,好多地方算错。
一、4.函数 f ( x , y ) = { x y 2 x 2 + y 4 x 2 + y 2 ≠ 0 0 x 2 + y 2 = 0 . f(x,y)= \\begin{cases} \\frac{xy^2}{x^2+y^4} && x^2+y^2≠0\\\\ 0 && x^2+y^2=0 \\end{cases} . f(x,y)={x2+y4xy20x2+y2=0x2+y2=0. 在 ( 0 , 0 ) (0, 0) (0,0)处()
A. 连续但偏导数不存在
B. 不连续但偏导数存在
C. 连续且偏导数存在
D. 不连续且偏导数不存
选B,这种题我一直不知道该咋做,说实话。不过,一般情况下都是选B。
三、6.设一平面上的力
F
=
(
x
,
y
)
\\textbf{F}=(x,y)
F=(x,y)作用在一质点上,该质点沿直线从
M
1
(
1
,
1
)
M_1(1, 1)
M1(1,1)移动到
M
2
(
2
,
2
)
M_2(2, 2)
M2(2,2),求力
F
\\textbf{F}
F所做的功.
这个题其实也挺简单,问题就在于,我把人家的
F
=
(
x
,
y
)
\\textbf{F}=(x,y)
F=(x,y)当成了一个函数
F
(
x
,
y
)
F(x, y)
F(x,y),眼睛瞎了属于是,人家是个向量,
x
x
x方向力为
x
x
x,
y
y
y方向力为
y
y
y,
W
=
∫
L
x
d
x
+
y
d
y
=
2
∫
1
2
x
d
x
=
3
W=\\int_Lxdx+ydy=2\\int^2_1xdx=3
W=∫Lxdx+ydy=2∫12xdx=3就完事儿了。这个故事告诉我们要心细一点。
二、8.求球面
x
2
+
y
2
+
z
2
=
4
x^2+y^2+z^2=4
x2+y2+z2=4在圆柱面
x
2
+
y
2
=
1
x^2+y^2=1
x2+y2=1内的面积。
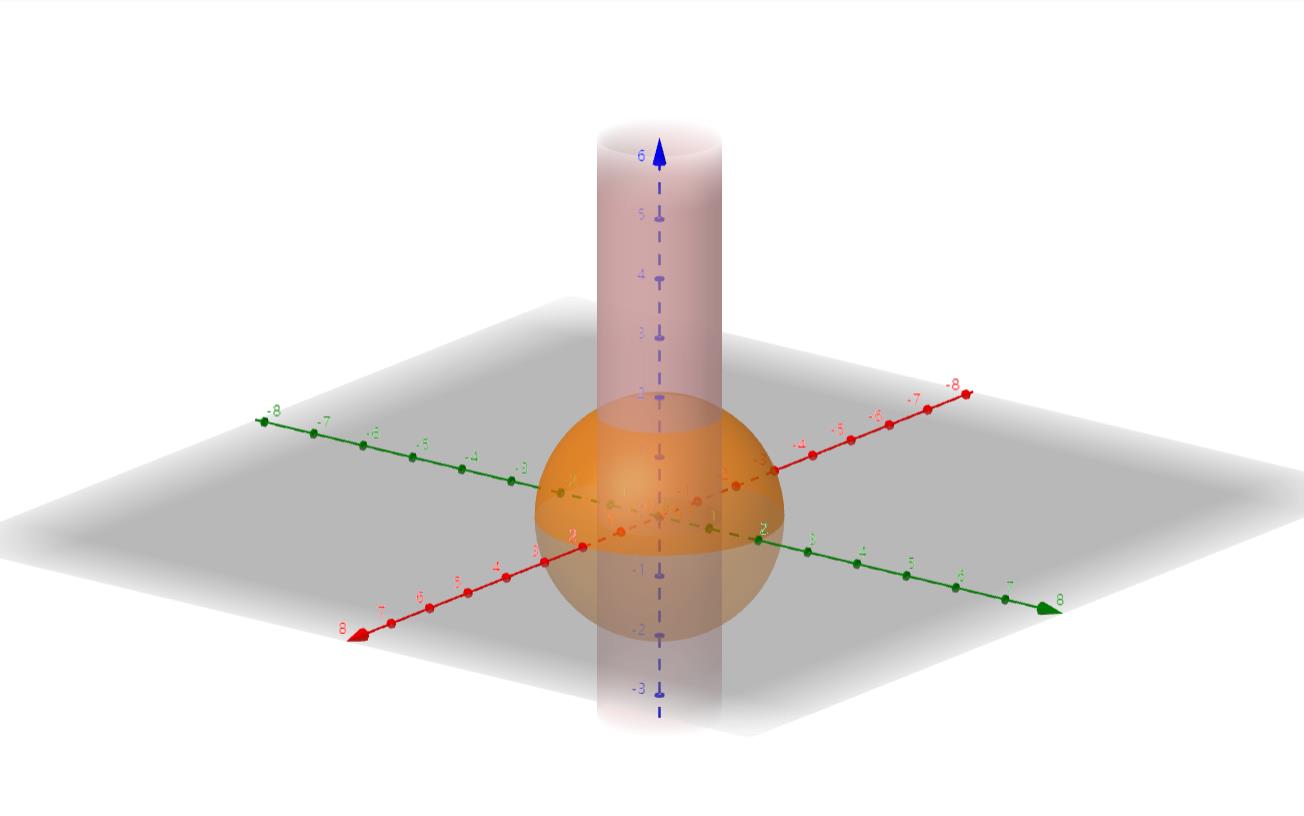
就像上面这个图像。
这个题题目审错了,以为是求体积,其实是求面积。求立体图形的表面积或表面积的一部分,一定要用第一类曲面积分。
求的就是上下那两片子的面积。
Σ
:
z
=
4
−
x
2
−
y
2
\\Sigma :z=\\sqrt{4-x^2-y^2}
Σ:z=4−x2−y2
(
x
,
y
)
∈
D
x
y
(x,y)\\in D_{xy}
(x,y)∈Dxy
z
x
=
−
x
4
−
x
2
−
y
2
z
y
=
−
y
4
−
x
2
−
y
2
z_x=\\frac{-x}{\\sqrt{4-x^2-y^2}}\\quad z_y=\\frac{-y}{\\sqrt{4-x^2-y^2}}
zx=4−x2−y2−xzy=4−x2−y2−y
D
x
y
:
x
2
+
y
2
≤
1
D_{xy}:x^2+y^2≤1
Dxy:x2+y2≤1
A
=
2
∬
Σ
d
S
A=2\\iint_\\Sigma dS
A=2∬ΣdS
=
2
∬
D
x
y
1
+
x
2
4
−
x
2
−
y
2
+
y
2
4
−
x
2
−
y
2
d
x
d
y
=2\\iint _{D_{xy}}\\sqrt{1+\\frac{x^2}{4-x^2-y^2}+\\frac{y^2}{4-x^2-y^2}}dxdy
=2∬Dxy1+4−x2−y2x2+4−x2−y2y2dxdy
=
4
∫
0
2
π
d
θ
∫
0
1
ρ
4
−
ρ
2
d
ρ
=4\\int_0^{2\\pi}d\\theta\\int^1_0\\frac{\\rho}{\\sqrt{4-\\rho^2}}d\\rho
=4∫02πdθ∫014−ρ2