C. Planar Reflections动态规划图解——CodeCraft-21 and Codeforces Round #711 (Div. 2)

Posted 2021-07-19 出尘呢

C. Planar Reflections
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
Gaurang has grown up in a mystical universe. He is faced by n consecutive 2D planes. He shoots a particle of decay age k at the planes.

A particle can pass through a plane directly, however, every plane produces an identical copy of the particle going in the opposite direction with a decay age k−1. If a particle has decay age equal to 1, it will NOT produce a copy.

For example, if there are two planes and a particle is shot with decay age 3 (towards the right), the process is as follows: (here, D(x) refers to a single particle with decay age x)

the first plane produces a D(2) to the left and lets D(3) continue on to the right;
the second plane produces a D(2) to the left and lets D(3) continue on to the right;
the first plane lets D(2) continue on to the left and produces a D(1) to the right;
the second plane lets D(1) continue on to the right (D(1) cannot produce any copies).
In total, the final multiset S of particles is {D(3),D(2),D(2),D(1)}. (See notes for visual explanation of this test case.)

Gaurang is unable to cope up with the complexity of this situation when the number of planes is too large. Help Gaurang find the size of the multiset S, given n and k.

Since the size of the multiset can be very large, you have to output it modulo 109+7.

Note: Particles can go back and forth between the planes without colliding with each other.

Input
The first line of the input contains the number of test cases t (1≤t≤100). Then, t lines follow, each containing two integers n and k (1≤n,k≤1000).

Additionally, the sum of n over all test cases will not exceed 1000, and the sum of k over all test cases will not exceed 1000. All test cases in one test are different.

Output
Output t integers. The i-th of them should be equal to the answer to the i-th test case.

Examples
inputCopy
4
2 3
2 2
3 1
1 3
outputCopy
4
3
1
2
inputCopy
3
1 1
1 500
500 250
outputCopy
1
2
257950823
Note
Let us explain the first example with four test cases.

Test case 1: (n=2, k=3) is already explained in the problem statement.

See the below figure of this simulation. Each straight line with a different color represents the path of a different particle. As you can see, there are four distinct particles in the multiset. Note that the vertical spacing between reflected particles is for visual clarity only (as mentioned before, no two distinct particles collide with each other)

Test case 2: (n=2, k=2) is explained as follows:

the first plane produces a D(1) to the left and lets D(2) continue on to the right;
the second plane produces a D(1) to the left and lets D(2) continue on to the right;
the first plane lets D(1) continue on to the left (D(1) cannot produce any copies).
Total size of multiset obtained {D(1),D(1),D(2)} is equal to three.

Test case 3: (n=3, k=1), there are three planes, but decay age is only one. So no new copies are produced while the one particle passes through the planes. Hence, the answer is one.

Test case 4: (n=1, k=3) there is only one plane. The particle produces a new copy to the left. The multiset {D(2),D(3)} is of size two.

思路：DP是一种思想

在这里，很多人可能都会以k++,n++为动态规划，打表
状态转移方程：

m[k][n]=m[k][n-1]+m[k-1][n-1]

意思是，从n-1层加到n层，就反射回去一个k-1强度的在n-1层中
可惜这是错掉的
错误的原因在于没有考虑反射回去的那一个再次反射到第n层上

这里正确的DP思路应该是考虑反射回去的那个吗，那无穷无尽了不叫DP

但是我们控制变量法，找到问题——添加实际层——能忽略就是正解
——有的时候就是要有这种大胆的精神，我发现了我的错误，我要把我错的把柄销毁
——于是就可以产生现在这个方法：
固定实际层，增加的是观察层

我们虽然不能一遍预处理，但是这样分别控制了n，可以对了

//这个dp是在n层的特定条件下的 

以下实际层为n，观察层为j，在这里按从出射向来处顺序，依次包含
初始条件：k=1时，或，j=0时，必定为1
迭代条件：

m[k][j]=m[k][n-j]+m[k-1][j]

——注意：n-j代表调换方向
变换的几何意义如下

以n=3,k=4为例演示
重点在后面一张发现反弹回去的已经被算在内了

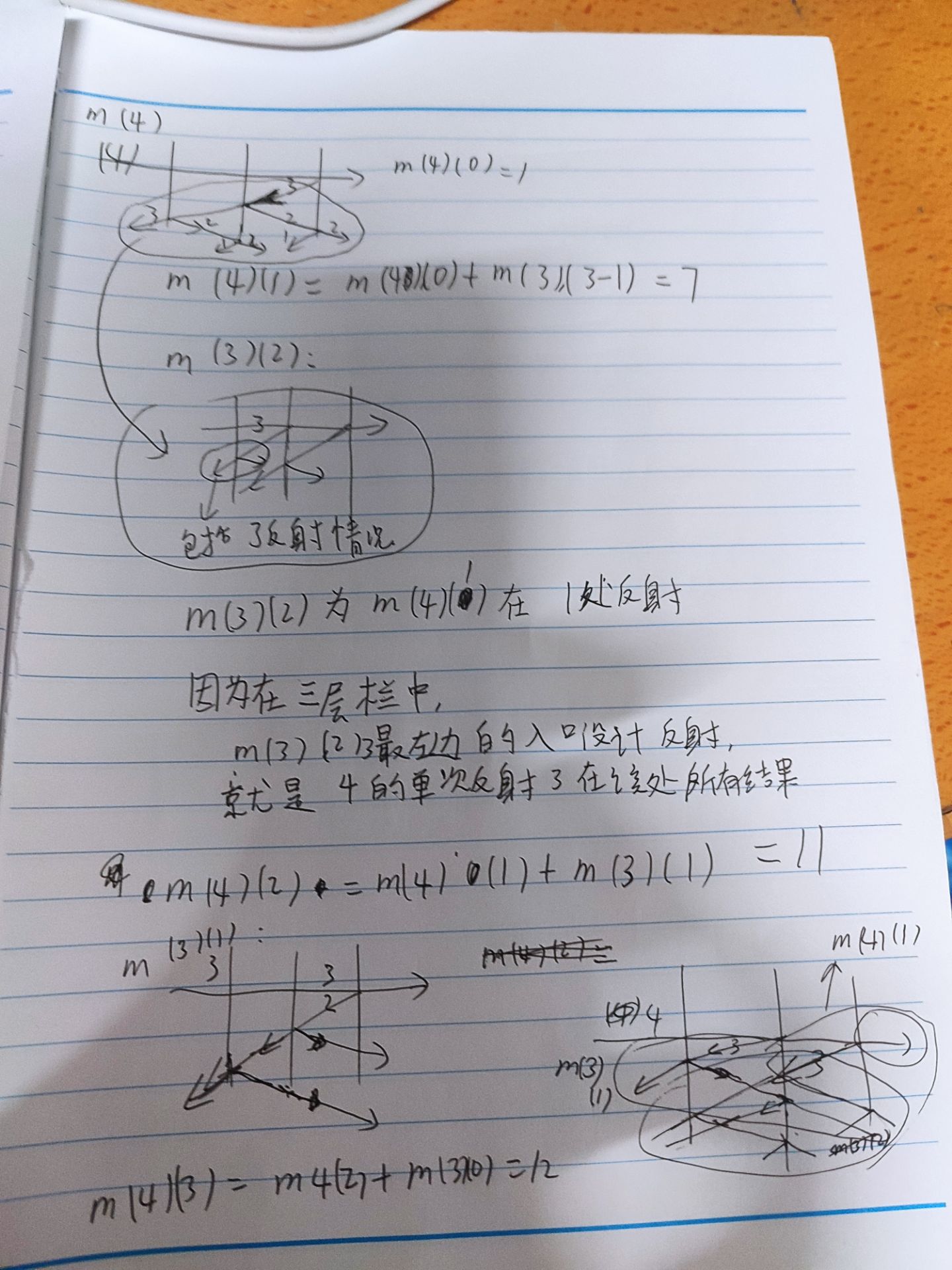
思考：为什么要从出射点往来路观察？
——由于子结构要在下一次迭代中可以应用

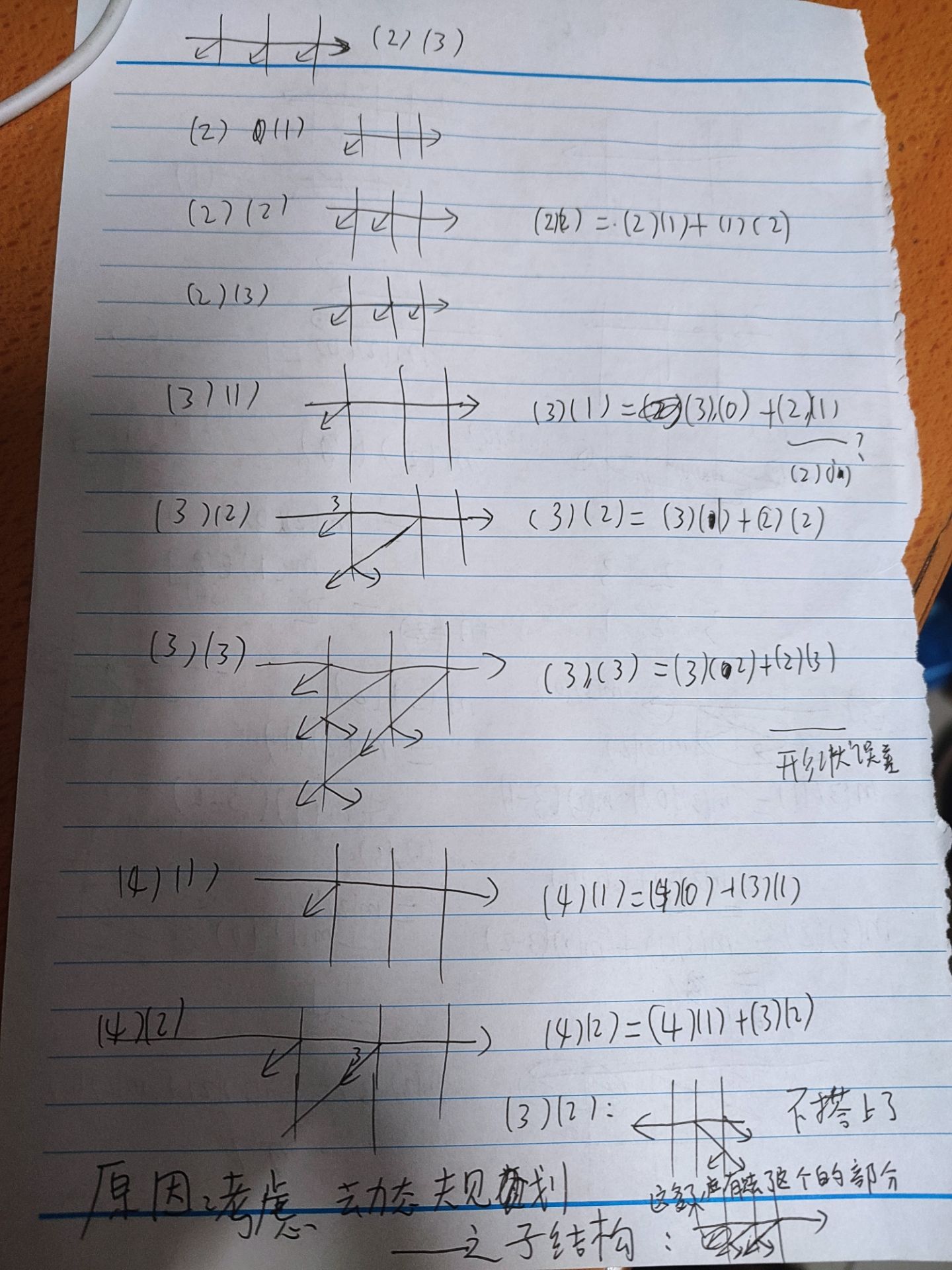
AC代码如下，31ms：

#pragma GCC optimize(3,"Ofast","inline")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<math.h>
#include<iostream>
#include<algorithm>
//#include<string>
//#include<sstream>
#include<vector>
#include<map>
//#include<set>
//#include<ctype.h>
//#include<stack>
//#include<queue>
#ifdef LOCAL
FILE*FP=freopen("text.in","r",stdin);
//FILE*fp=freopen("text.out","w",stdout);
#endif
using namespace std;
#define ll int
#define ld long double
#define pii pair<int,int>
#define piii pair<int,pii>
#define pll pair<ll,ll>
#define plll pair<ll,pll> 
#define pdd pair<double,double>
#define pdi pair<double,int>
#define pid pair<int,double>
#define vi vector <int> 
#define vii vector <vi> 
#define vl vector<ll>
#define st first
#define nd second
#define pb push_back
#define mp make_pair
#define mem(a,b) memset(a,b,sizeof(a))
#define _forplus(i,a,b) for( register int i=(a); i<=(b); i++)
#define forplus(i,a,b) for( register int i=(a); i<(b); i++)
#define _forsub(i,a,b) for( register int i=(a); i>=(b); i--)
#define _forauto(a,b) for(auto &(a):(b))
#define _forautome(a,b,c) for(auto (a) = (b); (a) != (c); (a)++)
#define ALL(x) x.begin(),x.end()
#define INS(x) inserter(x,x.begin())
#define INF 0x3f3f3f3f
#define LINF 0x3f3f3f3f3f3f3f3f
#define pi (acos(-1))
#define EPS 0.00000001
#define MOD (int)(1e9+7)
#define fastio 	std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);
#define N 1005
ll m[N][N];
ll t,n,k; 
void solve(){
	_forplus(i,0,n){
		m[1][i]=1;
	}
	_forplus(i,1,k){
		m[i][0]=1;
	}
	_forplus(i,2,k){//这个dp是在n层的特定条件下的 
		_forplus(j,1,n){
			m[i][j]=(m[i][j-1]+m[i-1][n-j])%MOD;
		}
	}
}
int main(){
	fastio
	cin>>t;
	while(t--){
		cin>>n>>k;
		solve();
		cout<<m[k][n]<<endl;
	}
	return 0;
}