DP从入门到精通2.1(线性DP,上升子序列,公共子序列)
Posted 芜湖之肌肉金轮
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了DP从入门到精通2.1(线性DP,上升子序列,公共子序列)相关的知识,希望对你有一定的参考价值。
DP入门到精通系列
emmm,dp问题真的很有魔力,你想得到状态表示方程,那么你马上就能起飞,如果你想不到,没思路那么......建议吃顿好的再来写可能会快点.....其实dp更多的是一种经验,你见得多,写的自然就快,因为这类题的状态表示你已经很熟悉了。好吧闲话不多说,继续dp之旅。
数字三角形
数字三角形也是一个经典的dp问题了,和背包一样非常常见,这种要归类的话,应该属于线性dp的一种,所谓线性dp就是说我们的dp方程(状态方程)是有一个明显的线性关系的(更新的时候呈线性)。那么数字三角形可以怎么去做呢?
给定一个如下图所示的数字三角形,从顶部出发,在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点,一直走到底层,要求找出一条路径,使路径上的数字的和最大。
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5数字三角形我们可以用两种方法来做,从上往下,或者从下往上:
从上往下
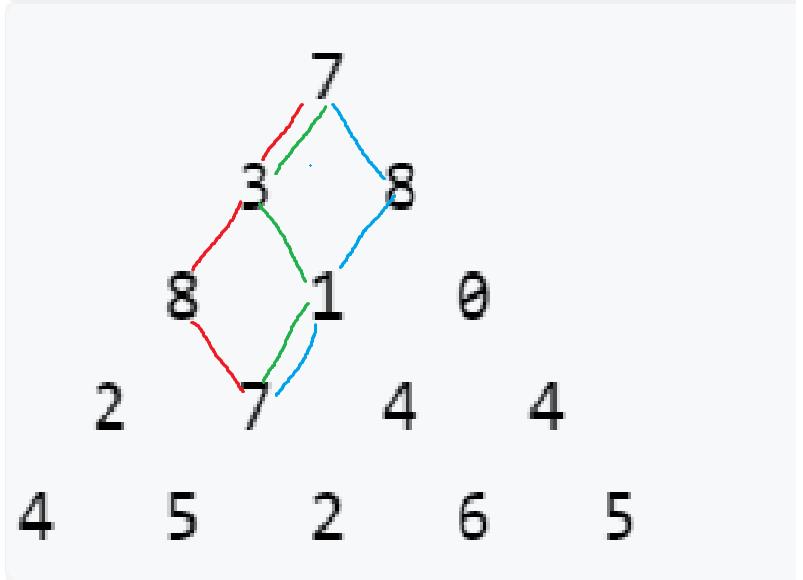
我们可以看出走到7这个点,我们可以从红 ,绿,蓝,三种路径到达,所以我们可以观察发现,走到7这个点的路径和要么来自左上,要么来自右上,既然如此我们就可以开始写我们状态方程了,为什么可以直接写了,因为dp——动态规划,其实就是一种处理具有相似特征的子问题的方法。
状态方程:f [ i ][ j ]=max(左上+a[ i ][ j ],右上+a[ i ][ j ])
状态表示:走到i,j的路径和的最大值
那么这个问题就好写了:
const int N = 510;
int f[N][N];
int a[N][N];
int n;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++) scanf("%d",&a[i][j]);
for(int i=0;i<=n;i++)
for(int j=0;j<=i+1;j++)//考虑到边界问题初始化的时候要注意多初始化一个地方防止最右边的数取来自右上角的数的时候出现边界问题
f[i][j]=-10000;
f[1][1]=a[1][1];
for(int i=2;i<=n;i++)
for(int j=1;j<=i;j++)
f[i][j]=max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j]);
int res=-10000;
for(int i=1;i<=n;i++)res=max(res,f[n][i]);
printf("%d",res);
return 0;
}从下到上
相比较于从上倒下,其实更加的简单,且好思考,因为不用考虑边界问题。
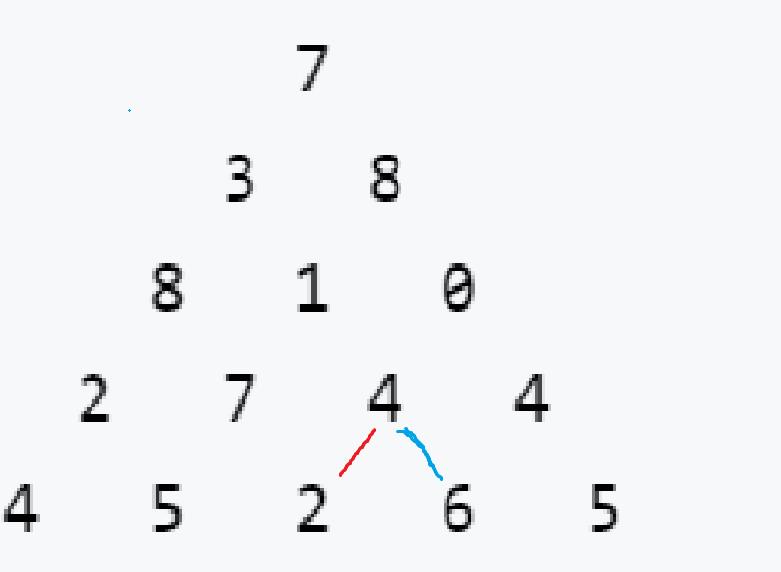
因为大致思路还是跟从上到下差不多,所以直接上代码了:
const int N = 510;
int f[N][N];
int a[N][N];
int n;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++) scanf("%d",&a[i][j]);
for(int i=n;i>=1;i--)
for(int j=1;j<=i;j++)
f[i][j]=max(f[i+1][j]+a[i][j],f[i+1][j+1]+a[i][j]);
printf("%d",f[1][1]);
return 0;
}
最长上升子序列
说实话做到最长上升子序列的时候,我才感受到线性dp的奇妙,线性dp刚才说过,是一种状态方程具有线性的一种dp,刚才的数字三角形可能不是那么明显,那么这道题可以让我们更接近线性dp的本质。
给定一个长度为 N 的数列,求数值严格单调递增的子序列的长度最长是多少。
看见一个dp问题我们肯定是要先想它的状态表示是什么,假如我们用二维去想:从 i 到 j ,以j结尾的上升子序列长度。这样子去想的话,我们可以发现 i 是不会动的,因为就算你动,我们求最长,你还是要加上 i 前面的数,所以我们可以直接优化到一维,从而变成以 j 结尾的上升子序列长度。有了状态表示,那么怎么更新呢,因为是最长,所以直接取max就好了。
int a[N],f[N];
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];//读入序列
for(int i=1;i<=n;i++)
{
f[i]=1;//加入只有该数本身,就是长度为1的子序列
for(int j=1;j<i;j++)
if(a[i]>a[j])
f[i]=max(f[i],f[j]+1);
}
int ans=0;
for(int i=1;i<=n;i++)ans=max(ans,f[i]);
cout<<ans;
return 0;
}但是假如数据给的大一点,比如100000,那么我们o(n^2)就会跑到10的10次方,必定超时,这种没有优化的dp就过不了了,那么有什么方法去优化吗,确实是有的,用二分是可以取优化的,但是优化之后,就不是很像dp(思路是由dp转变的)了所以暂时放一放,对于大数据的上升子序列之后再说。
最长公共子序列
给定两个长度分别为 N 和 M 的字符串 A 和 B,求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。
这类题说实话没见过,状态方程真的难写,但是回忆一下上一题的最长上升子序列的状态表示:以 j 结尾的上升子序列长度。我们是不是也可以一葫芦画瓢把这题的状态表示写成两个分别用以 j 结尾和以 i 结尾的两个子序列f[ i ],f[ j ]去表示其最长公共子序列呢?或许是可以的,但是两个方程如果分开写的话更新起来会很麻烦,而且不好作比较。但我们的思路是对的,那为什么不把他们合起来呢?状态表示依旧是以 j 结尾和以 i 结尾最长公共子序列,但状态方程不再是两个一维,而是变成一个二维的f[ i ][ j ],这样子似乎可以少很多很繁琐的比较步骤,从而让我们的重心落在分别以i, j结尾的两个子序列上。
状态表示之后,就是状态计算,让我们我想一下状态有什么: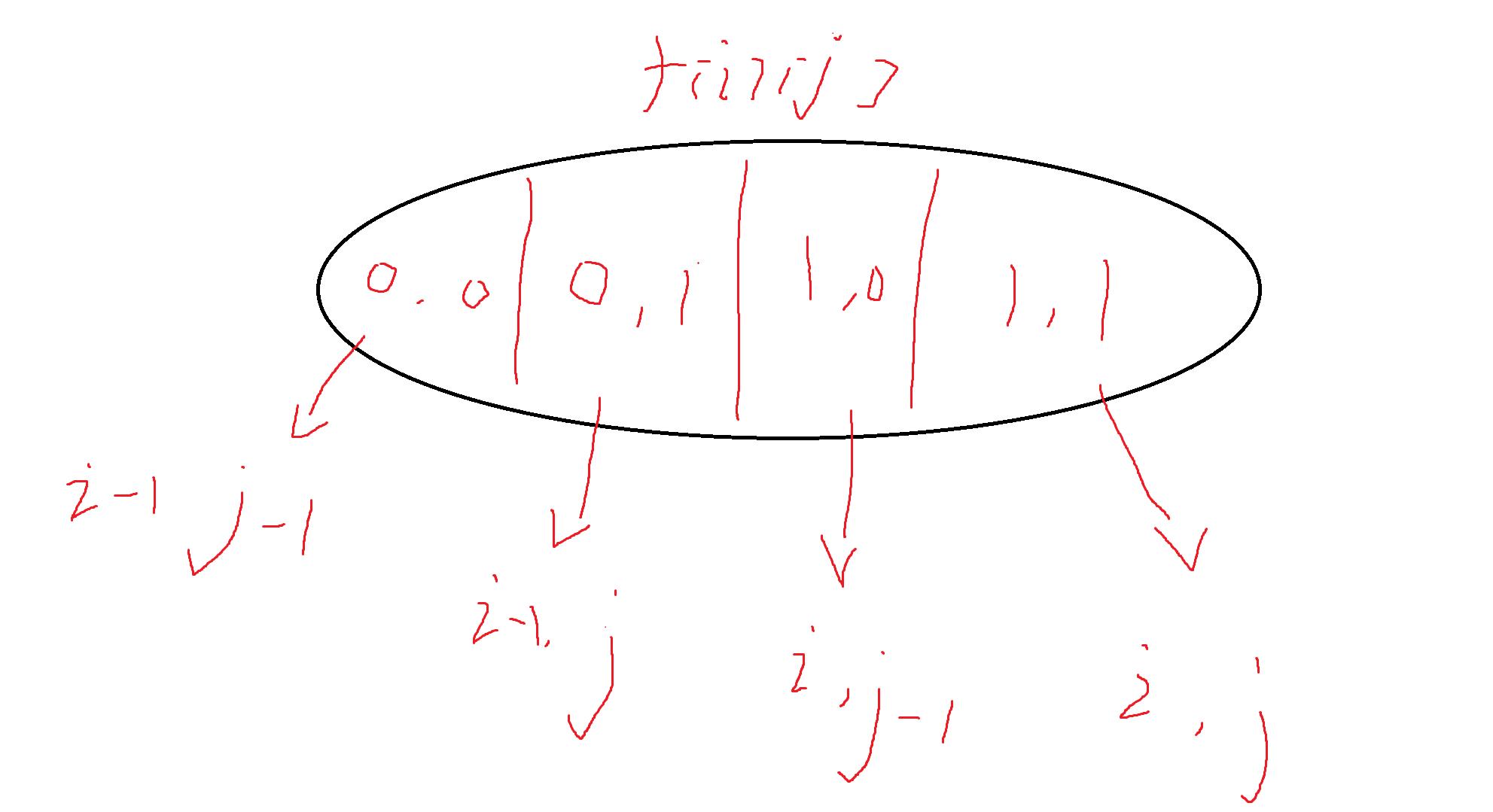
这里0代表不选,1代表选——所以我们发现这里有四个状态,所以我们给这四个状态取一个max就可以了,这里其实也是可以优化的因为我们在计算第二和第三个状态的时候就依旧把第一个状态给覆盖了,所以其实可以转变成二,三,四这三个状态(状态四只有当以结尾的i和结尾的j相等时才存在即a[i]==b[j]):
const int N = 1010;
string a,b;
int f[N][N];
int n,m;
int main()
{
cin>>n>>m>>a>>b;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
f[i][j]=max(f[i-1][j],f[i][j-1]);//二,三状态取max
if(a[i-1]==b[j-1])f[i][j]=max(f[i][j],f[i-1][j-1]+1);//二,三状态的max和状态四取max
}
cout<<f[n][m];
return 0;
}到这还是要感叹一下y总的思路实在是太清晰了,以上就是在acwing学习的一点小心得吧,希望能帮到大家(最长公共子序列的集合划分借鉴于y总)。
以上是关于DP从入门到精通2.1(线性DP,上升子序列,公共子序列)的主要内容,如果未能解决你的问题,请参考以下文章