AVL树
Posted Moua
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了AVL树相关的知识,希望对你有一定的参考价值。
目录
一、AVL树的概念
1、什么是AVL树?
当数据有序或者接近有序时,使用二叉搜索树进行存储时,得到的二叉搜索树是一颗单支树,其搜索的时间复杂度为O(N)。
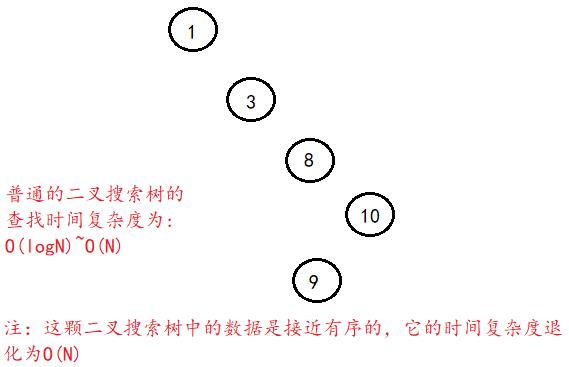
为了解决上述问题,引入了AVL树的概念:
- AVL树是一颗特殊的二叉搜索树
- 向AVL树中插入一个节点后,树的所有节点的左右孩子节点的高度差的绝对值小于等于1.
- 即AVL树是一颗二叉搜索树是,它的左右子子树的高度之差(平衡因子)的绝对值不大于1,并且它的左右子树也是一颗AVL树。
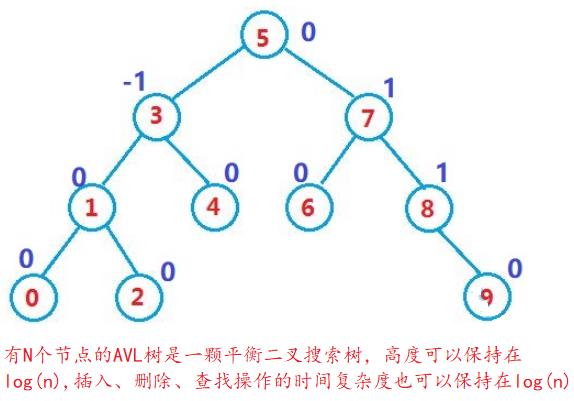
2、AVL树的节点定义
template<class T>
struct TreeNode
{
//构造函数
TreeNode(const T& val)
:_val(val),_bf(0),_left(nullptr),_right(nullptr),_parent(nullptr)
{}
T _val;
TreeNode* _left;//左孩子
TreeNode* _right;//右孩子
TreeNode* _parent;//双亲节点,不是必须的,为了方便实现而引入的
int _bf;//平衡因此,不是必须的,为了方便实现引入的。规定,左子树比右子树高平衡因子为-1,一样高为0,右高为1
};
二、AVL树的插入操作
AVL树也是一颗二叉搜索树,因此它在插入数据时也需要先找到要插入的位置然后在将节点插入。不同的是,AVL树插入节点后需要对节点的平衡因子进行调整,如果插入节点后平衡因子的绝对值大于1,则还需要对该树进行旋转,旋转成为一颗高度平衡的二叉搜索树。
1、插入节点
该步和二叉搜索树一样,先找到节点在进行插入。需要注意的是,如果是空树直接插入并且让树的根节点等于当前节点。
//1.找到该节点并插入
Node* newNode = new Node(val);
//如果是一颗空树,新插入节点就为跟节点
if(root == nullptr)
{
root = newNode;
return make_pair(root,true);
}
//找到插入位置
Node* parent = nullptr;//当前节点的父节点
Node* cur = root;
while(cur)
{
if((cur->_val).first < (newNode->_val).first)
{
//左走
parent = cur;
cur = cur->left;
}
else if((cur->_val).first > (newNode->_val).first)
{
//右走
parent = cur;
cur = cur->right;
}
else
{
//找到了,不需要插入,直接返回
return make_pair(cur,false);
}
}
//插入节点
if((parent->_val).first > (newNode->_val).first)
{
//插入到parent的左孩子节点处
parent->left = newNode;
newNode->_parent = parent;
return make_pair(newNode,true);
}
else
{
//插入到parent的右孩子节点处
parent->right = newNode;
newNode->_parent = parent;
return make_pair(newNode,true); }2、调整平衡因子
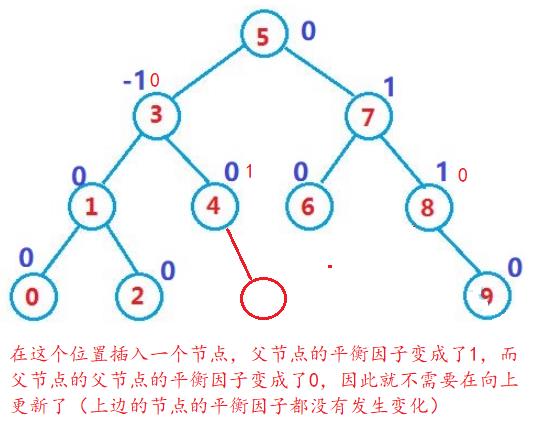
- 插入一个一个节点,只会影响根节点到插入节点的父节点上的平衡因子。
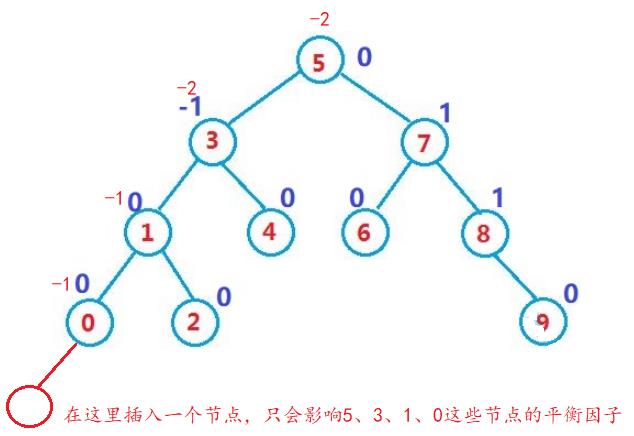
- 如果插入一个节点后,插入节点的父节点的平衡因子变成了0,则说明插入节点后树的高度没有发生变化,则只影响了父节点的平衡因子。
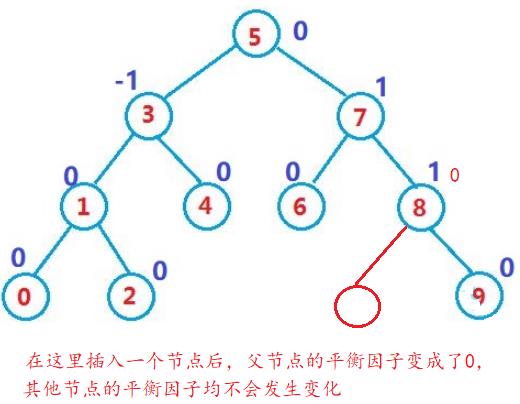
- 如果插入一个节点后,该节点的父节点的平衡因子的绝对值大于等于1,在向上更新过程中如果某一个节点的平衡因子变成了0则停止更新,最坏情况下一直要更新到根节点。
代码实现:
//2.调节平衡因子
/*基本思路
* 从该节点的父节点开始调整,如果父节点的平衡因子变成了0,则停止调整
* 如果该节点的父节点的平衡因子不是0,则继续向上调整,直到某个节点的
* 平衡因子变成0或者调整到了根节点
* 调整平衡因子的策略是,如果插入的节点是该节点的左孩子节点则平衡因子-1
* 如果是该节点的右孩子节点,则平衡因子+1
*/
cur = newNode;
while(parent)
{
if(cur == parent->left)
{
//parent的平衡因子-1
parent->_bf--;
}
else
{
//parent的平衡因子+1
parent->_bf++;
}
//判断parent的平衡因子是否为0
if(parent->_bf == 0)
{
//调整完成
break;
}
else
{
//继续调整parent的父节点
parent = parent->_parent;
} }3、旋转成为一颗AVL树
向AVL树中插入一个节点后,节点的平衡因子可能会发生变化,因此需要对节点的平衡因子进行调整。但是,调整后的节点的平衡因子可能会大于1,也就是说插入一个节点后不在是一颗AVL树。因此,需要通过旋转将调整后的树旋转成一颗AVL树。
1)右单旋:新插入的节点是较高的左子树的左孩子节点
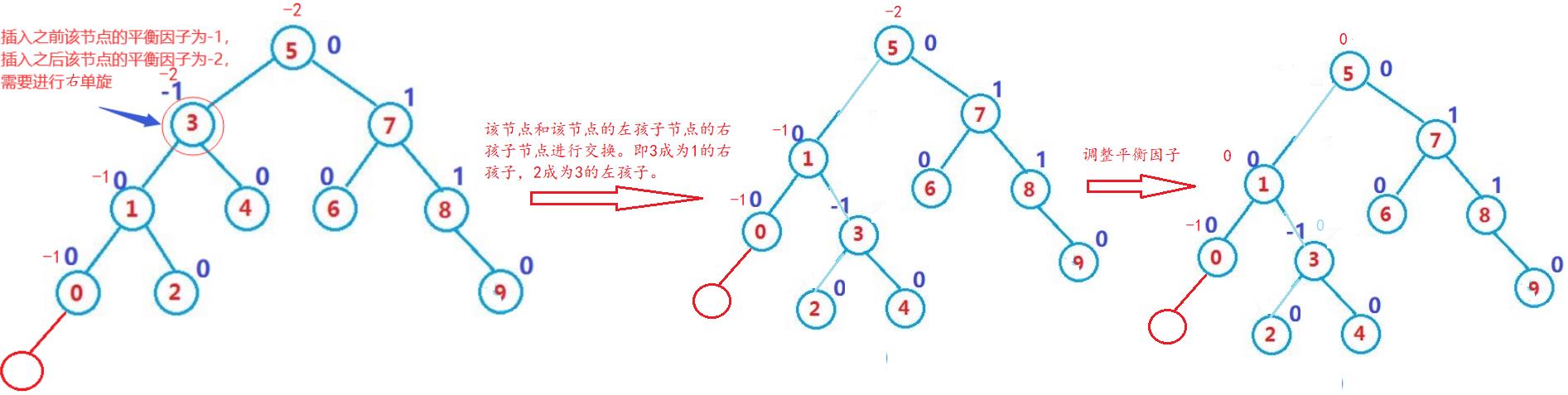
思考:如果新插入的节点是2的孩子节点,可以使用右单旋吗?
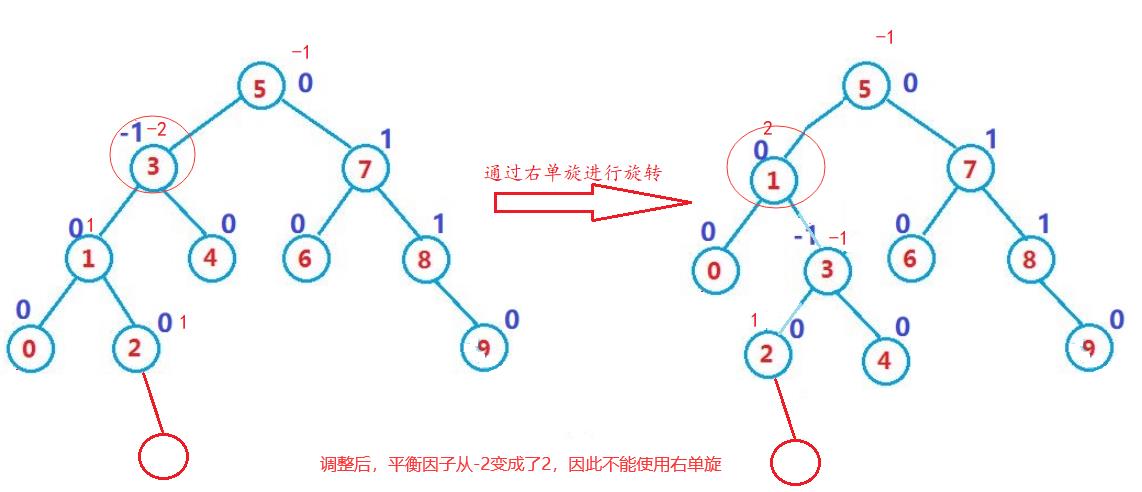
注意:要插入的节点必须是较高的左子树(对于-2来说,较高的左子树的根节点是1)的左孩子节点(对于1来说左孩子节点的根节点必须是0),因此当插入到2的时候不能使用右单旋。这时就需要使用左右单旋。
代码描述:
//右单旋
void RotateR(Node* parent)
{
Node* parentL = parent->_left;//parent的左孩节点
Node* subR = parentL->_right;//parent的左孩子节点的右孩子节点
Node* parentParent = parent->parent;
//parent的左孩子节点指向parentL的右孩子节点
parentL = subR;
if(subR)
subR->_parent = parent;
//parent变成parentL的右孩子节点
subR = parent;
//parent的父节点变成parent的左孩子节点
parent->_parent = parentL;
//parent是根节点
if(parent == root)
{
root = parentL;
root->_parent = nullptr;
}
else
{
if(parent == parentParent->_left)
{
parentParent->_left = parentL;
parentL->_parent = parentParent;
}
else
{
parentParent->_right = parentL;
parentL->_parent = parentParent;
}
}
parent->_bf = parentL->_bf = 0; }
2)左单旋:新插入节点是较高的右子树的右孩子节点
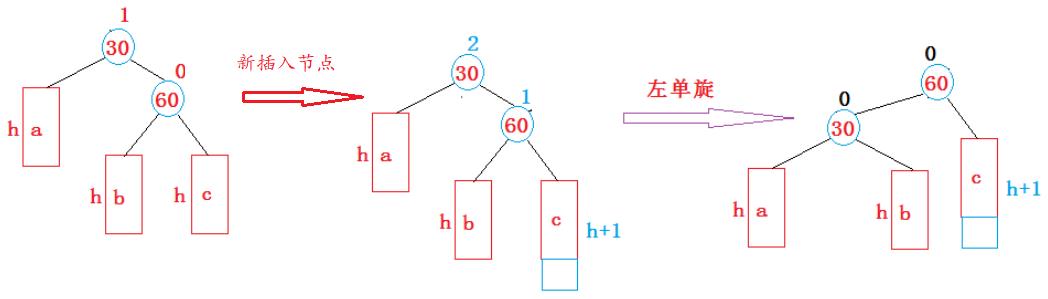
注意:如果新插入的节点是较高的右子树的左孩子节点时需要使用右左单旋
代码描述
//左单旋
void RotateL(Node* parent)
{
Node* parentR = parent->_right;//parent的右孩子节点
Node* subRL = parentR->_left;//parent的右孩子的左孩子节点
Node* parentParent = parent->_parent;
//parent的右孩子节点指向parent的右孩子节点的左孩子节点
parentR = subRL;
if(subRL)
subRL->_parent = parentR;
//parent的右孩子节点的左孩子节点指向parent节点
subRL = parent;
//parent的父节点指向parent的右孩子节点
parent->_parent = parentR;
if(parent == root)
{
root = parentR;
root->_parent = nullptr;
}
else
{
if(parentParent->_left == parent)
{
parentParent->_left = parent;
}
else
{
parentParent->_right = parent;
}
arent->_parent = parentParent;
}
parent->_bf = parentR->_bf = 0;
}
3)左右单旋:新插入节点是较高的左子树的右孩子节点
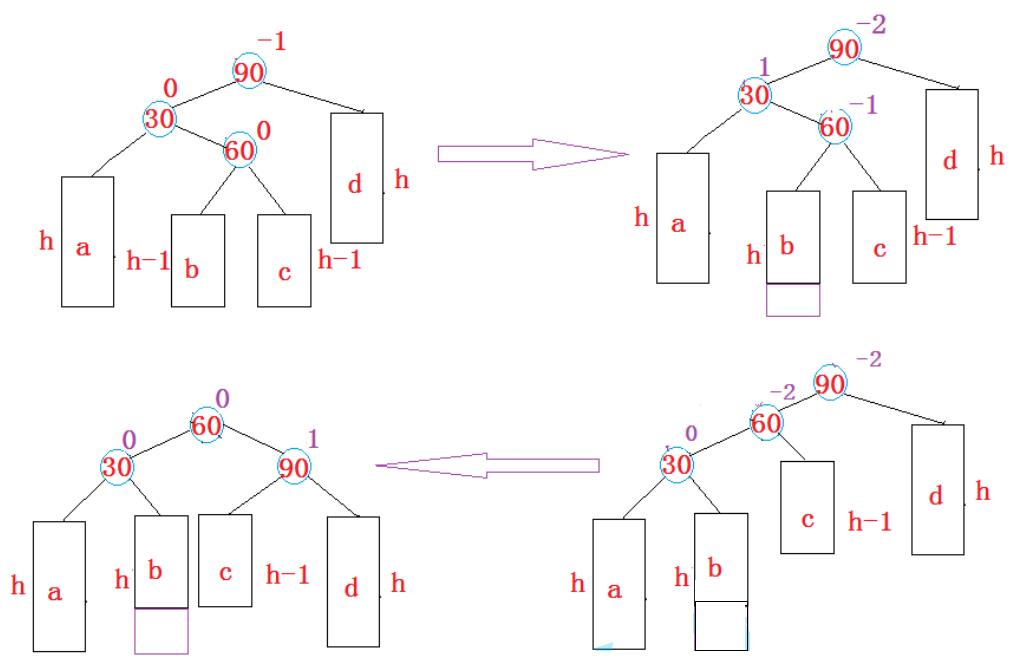
注意:左右单旋是指先对该节点的左孩子节点进行左单旋,在对该节点进行右单旋
代码描述
//左右单旋
void RotateLR(Node* parent)
{
Node* parentL = parent->_left;
Node* subLR = parentL->_right;
int subLRBf = subLR->_bf;
//左孩子节点进行左单旋
RotateL(parent->_left);
RotateR(parent);
//调整平衡因子
if(subLRBf == 1)
{
parent->_bf = subLR->_bf = 0;
parentL->_bf = -1;
}
else if(subLRBf == -1)
{
subLR->_bf = parentL->_bf = 0;
parent->_bf = -1;
}
else
{
parent->_bf = parentL->_bf = subLR->_bf = 0;
}
}4)右左单旋:新插入节点在较高右子树的左孩子节点
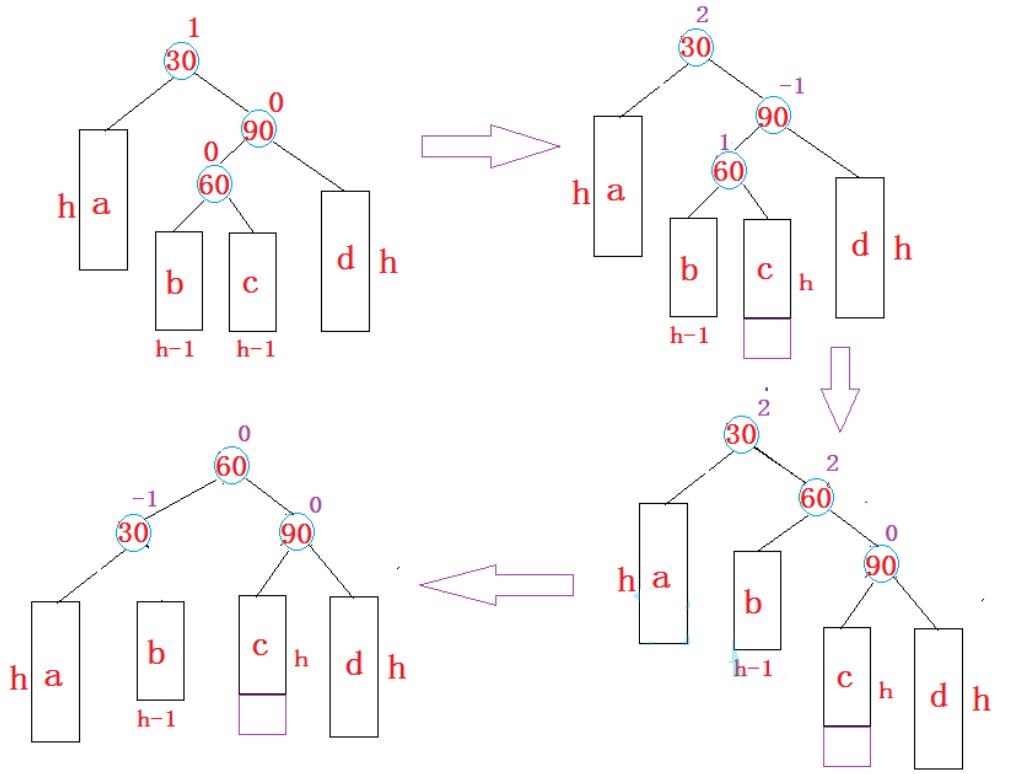
代码描述
//右左单旋
void RotateRL(Node* parent)
{
Node* parentR = parent->_right;
Node* subRL = parentR->_left;
int subRLBf = subRL->_bf;
//该节点的右孩子进行右旋转
RotateR(parent->_right);
//该节点进行左旋转
RotateL(parent);
//调整平衡因子
if(subRLBf == 1)
{
parentR->_bf = subRL->_bf = 0;
parent->_bf = -1;
}
else if(subRLBf == -1)
{
parentR->_bf = subRL->_bf = 0;
parent->_bf = 1;
}
else
{
parentR->_bf = subRL->_bf = parent->_bf = 0;
} } 5)验证
验证一颗二叉树是否是AVL树时,只要满足以下两个方面就说明该二叉树是AVL树:
- 该二叉树是一颗二叉搜索树:中序遍历得到有序序列
- 是否是平衡的:左右子树的平衡因子之差的绝对值小于等于1;插入节点、旋转之后平衡因子是否更新正确、
代码描述
//中序遍历AVL树
static void BSTreeInOrder(Node* node,vector<pair<K,V>>& inOrder)
{
//inOrder是输出型参数,将遍历结果保存到该数组中
if(node == nullptr)
return;
BSTreeInOrder(node->_left,inOrder);
inOrder.push_back(node->_val);
BSTreeInOrder(node->_right,inOrder);
}
bool isBSTree()
{
vector<pair<K,V>> inOrder; BSTreeInOrder(root,inOrder);
if(inOrder.empty())
return true;
//遍历,检查是否有序
pair<K,V> tmp = inOrder[0];
for(int i = 1;i < inOrder.size();i++)
{
if(tmp.first < inOrder[i].first)
{
tmp = inOrder[i];
}
else
return false;
}
}
//二叉树的高度
static int BSTreeHeight(Node* node)
{
if(node == nullptr)
return 0;
int left = BSTreeHeight(node->_left);
int right = BSTreeHeight(node->_right);
return left>right?(left+1):(right+1);
}
//判断是否平衡
static bool _isBalance(Node* root)
{
//求左右子树的高度
int left = BSTreeHeight(root->_left);
int right = BSTreeHeight(root->_right);
if(abs(left-right) <= 1)
{
return _isBalance(root->_left) && _isBalance(root->_right); }
else
return false;
}
//验证AVL树
bool isBalance()
{
if(root == nullptr)
return true;
if(isBSTree() && _isBalance())
return true;
return false;
}三、AVL树的实现
#pragma once
#include<iostream>
#include<stdlib.h>
#include<vector>
using namespace std;
//节点定义
template<class K,class V>
struct AVLTreeNode
{
pair<K,V> _val;//节点,键值对
int _bf;//平衡因子
AVLTreeNode<K,V>* _left;//左子树
AVLTreeNode<K,V>* _right;//右子树
AVLTreeNode<K,V>* _parent;//双亲节点
AVLTreeNode(const pair<K,V>& val)
:_val(val),_bf(0)
,_left(nullptr),_right(nullptr),_parent(nullptr)
{}
};
template<class K,class V>
class AVLTree
{
typedef AVLTreeNode<K,V> Node;
private:
Node* root = nullptr;//根节点
public:
//构造函数
//析构函数
//插入--返回一个键值对,键值对的第一个值是插入节点的指针第二个值是bool值表示是否插入成功
pair<Node*,bool> insert(const pair<K,V>& val)
{ //1.找到该节点并插入
Node* newNode = new Node(val);
//如果是一颗空树,新插入节点就为跟节点
if(root == nullptr)
{
root = newNode;
return make_pair(root,true);
}
//找到插入位置
Node* parent = nullptr;//当前节点的父节点
Node* cur = root;
while(cur)
{
if((cur->_val).first < (newNode->_val).first)
{
//左走
parent = cur;
cur = cur->left;
}
else if((cur->_val).first > (newNode->_val).first)
{
//右走
parent = cur;
cur = cur->right;
}
else
{
//找到了,不需要插入,直接返回
return make_pair(cur,false);
}
}
//插入节点
if((parent->_val).first > (newNode->_val).first)
{
//插入到parent的左孩子节点处 parent->right = newNode;
newNode->_parent = parent;
}
//2.调整平衡因子
/*基本思路
* 从该节点的父节点开始调整,如果父节点的平衡因子变成了0,则停止调整
* 如果该节点的父节点的平衡因子不是0,则继续向上调整,直到某个节点的
* 平衡因子变成0或者调整到了根节点
* 调整平衡因子的策略是,如果插入的节点是该节点的左孩子节点则平衡因子-1
* 如果是该节点的右孩子节点,则平衡因子+1
*/
cur = newNode;
while(parent)
{
if(cur == parent->left)
{
//parent的平衡因子-1
parent->_bf--;
}
else
{
//parent的平衡因子+1
parent->_bf++;
}
//判断parent的平衡因子是否为0
if(parent->_bf == 0)
{
//调整完成
break;
}
else if(parent->bf == -1 || parent->bf == 1)
{ //继续向上调整
cur = parent;
parent = parent->_parent;
}
else
{
//已经不再是一颗AVL树,需要进行旋转
if(parent->_bf == -2)
{
if(parent->_left->_bf == -1)
{
//新插入的节点是较高的左子树的左孩子节点---右单旋
RotateR(parent);
}
else
{
//左右单旋
RotateLR(parent);
}
}
else if(parent->_bf == 2)
{
if(parent->_right->_bf == 1)
{
//左单旋
RotateL(parent);
}
else
{
//右左单旋
RotateRL(parent);
}
}
}
} return make_pair(cur,false);
}
//右单旋
void RotateR(Node* parent)
{
Node* parentL = parent->_left;//parent的左孩节点
Node* subR = parentL->_right;//parent的左孩子节点的右孩子节点
Node* parentParent = parent->parent;
//parent的左孩子节点指向parentL的右孩子节点
parentL = subR;
if(subR)
subR->_parent = parent;
//parent变成parentL的右孩子节点
subR = parent;
//parent的父节点变成parent的左孩子节点
parent->_parent = parentL;
//parent是根节点
if(parent == root)
{
root = parentL;
root->_parent = nullptr;
}
else
{
if(parent == parentParent->_left)
{
parentParent->_left = parentL;
parentL->_parent = parentParent;
}
else
{
parentParent->_right = parentL;
parentL->_parent = parentParent;
} }
parent->_bf = parentL->_bf = 0;
}
//左单旋
void RotateL(Node* parent)
{
Node* parentR = parent->_right;//parent的右孩子节点
Node* subRL = parentR->_left;//parent的右孩子的左孩子节点
Node* parentParent = parent->_parent;
//parent的右孩子节点指向parent的右孩子节点的左孩子节点
parentR = subRL;
if(subRL)
subRL->_parent = parentR;
//parent的右孩子节点的左孩子节点指向parent节点
subRL = parent;
//parent的父节点指向parent的右孩子节点
parent->_parent = parentR;
if(parent == root)
{
root = parentR;
root->_parent = nullptr;
}
else
{
if(parentParent->_left == parent)
{
parentParent->_left = parent;
}
else
{
parentParent->_right = parent;
} parent->_parent = parentParent;
}
parent->_bf = parentR->_bf = 0;
}
//左右单旋
void RotateLR(Node* parent)
{
Node* parentL = parent->_left;
Node* subLR = parentL->_right;
int subLRBf = subLR->_bf;
//左孩子节点进行左单旋
RotateL(parent->_left);
RotateR(parent);
//调整平衡因子
if(subLRBf == 1)
{
parent->_bf = subLR->_bf = 0;
parentL->_bf = -1;
}
else if(subLRBf == -1)
{
subLR->_bf = parentL->_bf = 0;
parent->_bf = -1;
}
else
{
parent->_bf = parentL->_bf = subLR->_bf = 0;
}
}
//右左单旋
void RotateRL(Node* parent)
{
Node* parentR = parent->_right;
Node* subRL = parentR->_left;
int subRLBf = subRL->_bf;
//该节点的右孩子进行右旋转
RotateR(parent->_right);
//该节点进行左旋转
RotateL(parent);
//调整平衡因子
if(subRLBf == 1)
{
parentR->_bf = subRL->_bf = 0;
parent->_bf = -1;
}
else if(subRLBf == -1)
{
parentR->_bf = subRL->_bf = 0;
parent->_bf = 1;
}
else
{
parentR->_bf = subRL->_bf = parent->_bf = 0;
}
}
//中序遍历AVL树
static void BSTreeInOrder(Node* node,vector<pair<K,V>>& inOrder)
{
//inOrder是输出型参数,将遍历结果保存到该数组中
if(node == nullptr)
return;
BSTreeInOrder(node->_left,inOrder);
inOrder.push_back(node->_val);
BSTreeInOrder(node->_right,inOrder);
}
bool isBSTree()
{
vector<pair<K,V>> inOrder; BSTreeInOrder(root,inOrder);
if(inOrder.empty())
return true;
//遍历,检查是否有序
pair<K,V> tmp = inOrder[0];
for(int i = 1;i < inOrder.size();i++)
{
if(tmp.first < inOrder[i].first)
{
tmp = inOrder[i];
}
else
return false;
}
}
//二叉树的高度
static int BSTreeHeight(Node* node)
{
if(node == nullptr)
return 0;
int left = BSTreeHeight(node->_left);
int right = BSTreeHeight(node->_right);
return left>right?(left+1):(right+1);
}
//判断是否平衡
static bool _isBalance(Node* root)
{
//求左右子树的高度
int left = BSTreeHeight(root->_left);
int right = BSTreeHeight(root->_right);
if(abs(left-right) <= 1)
{
return _isBalance(root->_left) && _isBalance(root->_right); }
else
return false;
}
//验证AVL树
bool isBalance()
{
if(root == nullptr)
return true;
if(isBSTree() && _isBalance())
return true;
return false;
}
}
以上是关于AVL树的主要内容,如果未能解决你的问题,请参考以下文章