DP棋盘分割

Posted 2021-07-18 Vincent_0000

题目来源

点我进入ACwing官网提交

题目描述

将一个 8×8 的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了 (n−1) 次后，连同最后剩下的矩形棋盘共有 n 块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

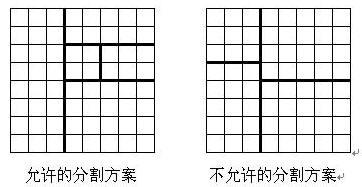
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。

现在需要把棋盘按上述规则分割成 n 块矩形棋盘，并使各矩形棋盘总分的均方差最小。

均方差
，其中平均值
，$x_i$ 为第 $i$ 块矩形棋盘的总分。

请编程对给出的棋盘及 n，求出均方差的最小值。

输入格式
第 1 行为一个整数 n。

第 2 行至第 9 行每行为 8 个小于 100 的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出格式
输出最小均方差值（四舍五入精确到小数点后三位）。

数据范围
1<n<15
输入样例：
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3
输出样例：
1.633

题目思路

• 题目大意

目标是将棋盘分割成n块，每切一次，只能挑选其中一个棋盘进行操作，给定方块中的值，求最小总方差。

• 分析题型

数据范围不太大，求最值，尝试使用DP。
根据形态可划分为两边，有分治的意思，尝试使用区间DP的思考方式解题。

• 分析动态转移方程

确定DP集合的性质，因为是分块的，且互不干扰，所以前四维代表左上角和右下角的坐标，因为只能切$n-1$次，有次数限制，所以还得加一维记录一下次数。所代表的值就是该区域的总方差值。（平均数就是总数/n，输入完就知道了平均值，再根据方差公式直接求解即可，用到了区间前缀和）
给定棋盘之后有两种切法，一种是横切，一种是纵切，切完之后还得挑选哪一部分做为下一次操作的情况。

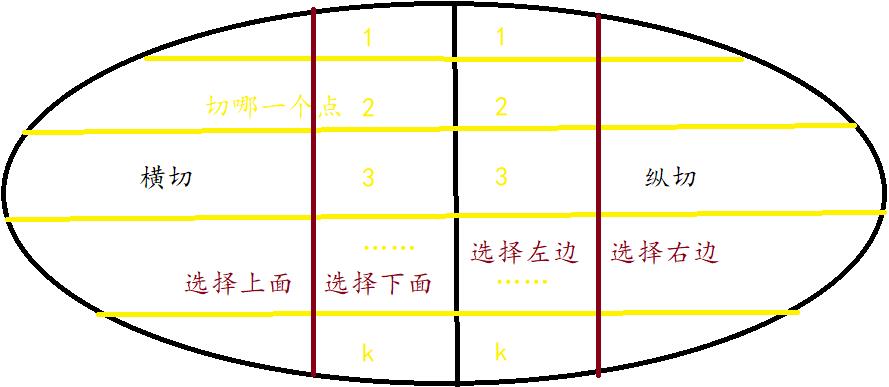
这个图简单明了，说明了所有的状态。

有点分治的味道，所以使用递归的方式写DP。

动态规划方程请看代码~

AC代码

#include<bits/stdc++.h> 
using namespace std;

#define _for(i, a, b) for (int i = (a); i < (b); ++i) 
#define _rep(i, a, b) for (int i = (a); i <= (b); ++i)
#define For(i, a, b) for (int i = (a); i >= (b); --i)
#define debug(a) cout << #a << " = " << a << ENDL
#define ENDL "\\n"
#define x first 
#define y second 
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;

const int N = 15 + 5, M = 8 + 5, INF = 0x3f3f3f3f;
int m = 8, n;
double X, s[M][M], f[M][M][M][M][N];

double Get(int x1, int y1, int x2, int y2) {
	double sum = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1] - X;
	return sum * sum / n;
}

double dp(int x1, int y1, int x2, int y2, int k) {
	double& v = f[x1][y1][x2][y2][k];
	if (v >= 0) return v;
	if (k == 1) return v = Get(x1, y1, x2, y2);

	v = INF;
	_rep(i, y1, y2) {
		v = min(v, Get(x1, y1, x2, i) + dp(x1, i + 1, x2, y2, k - 1));
		v = min(v, dp(x1, y1, x2, i, k - 1) + Get(x1, i + 1, x2, y2));
	}

	_rep(i, x1, x2) {
		v = min(v, Get(x1, y1, i, y2) + dp(i + 1, y1, x2, y2, k - 1));
		v = min(v, dp(x1, y1, i, y2, k - 1) + Get(i + 1, y1, x2, y2));
	}
	return v;
}

int main() {
#ifdef LOCAL
	freopen("data.in", "r", stdin);
#endif 
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);

	cin >> n;
	_rep(i, 1, m) _rep(j, 1, m) {
		cin >> s[i][j];
		s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
	}
	X = s[m][m] / n;
	
	memset(f, -1, sizeof f);
	printf("%0.3lf\\n", sqrt(dp(1, 1, m, m, n)));
	return 0;
} 

反思

这个题目因为做过一次，所以就没有认真看题目导致后面浪费了一堆时间！！
一定要注重做题第一步！！！！