斜率优化DP Cats Transport LibreOJ - 10187

Posted 2021-07-18 Vincent_0000

题目提交点

点我进入提交题目

题解

• 题目分析

① 有m 只猫，p个饲养员，n座山。
② 每个饲养员只能从第一座山开始走， 饲养员开始走的起始时间可以为负数。
③ 只能超过猫的玩耍时间才能带走该猫。
④ 求解最小的所有猫的最小等待时间总和。

求最小值，往动态规划DP 思路上面想，虽然刚开始会有点难度，不知道从哪里入手，多尝试一下，尝试不同的角度。
能不能快速找出题目的突破口，就看做题人的天赋或者刷题经验了，这题的突破口在于题目的抽象转化。

我们将性质转化一下，$d_i$表示从第一座山到第$i$座山的距离。那么就会有$Star{t}_i+d_i\ge t_i$，$Star{t}_i$为第$i$位饲养员开始的时间。将公式变形一下：$s_i\ge t_i-d_i$ 这样就写成关于开始时间的公式了。
我们令$a_i=t_i-d_i$并将其进行排序。
接下来就可以对开始时间进行处理，先以下面的这个为例，我们要将3、4、5点的猫咪一次带走，那么最好的方式就是令$Star{t}_i=a_i$这样的话，第5只猫咪对答案的贡献值就是最小，而其他的点也符合$Star{t}_i+d_i\ge t_i$这个条件。

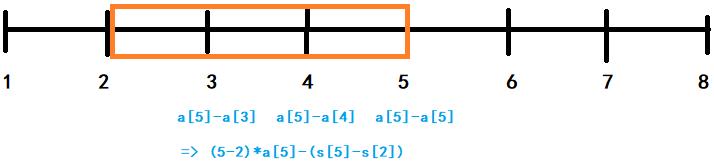
根据上图的例子我们就可以推导出它所对答案的贡献公式。
那么对于这个类型的题目，就已经转化为了任务安排题目了。

• 深入分析

根据上面的分析，我们可以将我们的集合设置为两维。
$f(i,j)$表示i个饲养员带走j只猫所积累的值。
动态规划方程可以写为： f ( i , j ) = m i n { f ( i − 1 , k ) + ( j − k ) ∗ a j − ( s j − s k ) } f(i, j) = min \\{ f(i-1, k) + (j - k) * a_j - (s_j - s_k) \\} f(i,j)=min{f(i−1,k)+(j−k)∗aj​−(sj​−sk​)}
$s$为$a$的前缀和。

将公式进一步变型可得：$f(i-1,k)+s_k=a_j\ast k-j\ast a_j+s_j-f(i,j)$
就可以进行斜率优化，x轴、y轴代表的值是单调递增的，斜率也是单调递增的，那么就可以使用任务安排1的思路进行解题。

AC代码

#include<bits/stdc++.h>
using namespace std;

#define _for(i, a, b) for (int i = (a); i <= (b); ++i)
#define _rep(i, a, b) for (int i = (a); i >= (b); --i)
#define debug(a) cout << #a << " = " << a << endl
#define mod(x) (x) % MOD
#define ENDL "\\n"
#define x first
#define y second
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;

const int N = 100000 + 7, M = 110, MOD = 1e9, INF = 0x3f3f3f3f;
ll f[M][N], d[N], s[N], a[N];
int q[N];

ll Y(int i, int k){
    return f[i - 1][k] + s[k];
}

int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
#endif
    ios::sync_with_stdio(false);
    cout.tie(0), cin.tie(0);

    int n, m, p;
    cin >> n >> m >> p;
    _for(i, 2, n) {
        cin >> d[i];
        d[i] += d[i - 1];
    }
    _for(i, 1, m) {
        int h, t;
        cin >> h >> t;
        a[i] = t - d[h];
    }
    sort(a + 1, a + m + 1);
    _for(i, 1, m) s[i] = s[i - 1] + a[i];

    memset(f, 0x3f, sizeof f);
    _for(i, 0, p) f[i][0] = 0;

    _for(i, 1, p){
        int hh = 0, tt = 0;
        q[0] = 0;

        _for(j, 1, m){
            while (hh < tt && Y(i, q[hh + 1]) - Y(i, q[hh]) <= a[j] * (q[hh + 1] - q[hh])) ++hh;
            int k = q[hh];
            f[i][j] = f[i - 1][k] + (j - k) * a[j] - s[j] + s[k];
            while (hh < tt && (Y(i, q[tt]) - Y(i, q[tt - 1])) * (j - q[tt - 1]) >= (q[tt] - q[tt - 1]) * (Y(i, j) - Y(i, q[tt - 1])))
                --tt;
            q[++tt] = j;
        }
    }
    cout << f[p][m] << ENDL;
    return 0;
}

总结

做DP题目要学会将思路抽象出来， 将一个题目转化成另一个题目，然后进行组装进行解题。