条件概率全概率公式
Posted 一只特立独行的猫
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了条件概率全概率公式相关的知识,希望对你有一定的参考价值。
条件概率
定义:
设A,B为两个事件,,且P(B)>0,则称P(A|B)=
P
(
A
B
)
P
(
B
)
\\frac {P(AB)}{P(B)}
P(B)P(AB)为事件B已经发生的条件下,事件A发生的概率,即
P
(
A
∣
B
)
=
P
(
A
B
)
P
(
B
)
P(A|B)=\\frac {P(AB)}{P(B)}
P(A∣B)=P(B)P(AB)
条件概率有如下性质:
1.任意A,P(AB)≥0
2.P(Ω|B)=1
3.
A
1
,
A
2
,
.
.
.
A
n
A_1,A_2,...A_n
A1,A2,...An两两互斥,则
P
(
∪
i
=
1
∞
A
i
)
=
∑
i
=
1
∞
P
(
A
i
)
P(\\overset{∞}{\\underset{i=1}{∪}}A_i)=\\overset{∞}{\\underset{i=1}{∑}}P(A_i)
P(i=1∪∞Ai)=i=1∑∞P(Ai)
4.P(∅|B)=0
5.P(
A
−
\\overset{-}{A}
A−|B)=1-P(A|B)
两种计算方法:
1.定义法
P
(
A
∣
B
)
=
P
(
A
B
)
P
(
B
)
P(A|B)=\\frac {P(AB)}{P(B)}
P(A∣B)=P(B)P(AB)
可以通过求的P(AB)和P(B)来求得A在B条件下的概率
2.样本空间缩减法
列出A和B的样本空间,并求的A和B中共同的样本C,并计算C在B中占的比例。
注:
一般情况下,P(A|B)≥P(AB),因为条件概率有约束条件,分母可能比1要小。
乘法定理:
设P(B)>0,有P(AB)=P(A|B)P(B)
可以在此进行推广:
三个事件 P(AB)>0 P(ABC)=P(A|BC)P(BC)=P(A|BC)P(B|C)P(C)
可以推广到n个事件:
若
P(
A
1
,
A
2
,
.
.
.
A
n
A_1,A_2,...A_n
A1,A2,...An)>0
则有
P(
A
1
,
A
2
,
.
.
.
A
n
A_1,A_2,...A_n
A1,A2,...An)=
P
(
A
1
)
P
(
A
2
∣
A
1
)
.
.
.
P
(
A
n
∣
A
n
−
1
.
.
.
A
1
)
P(A_1)P(A_2|A_1)...P(A_n|A_{n-1}...A_1)
P(A1)P(A2∣A1)...P(An∣An−1...A1)
全概率公式和贝叶斯公式
划分:
定义:
设Ω,
A
1
,
A
2
,
.
.
.
A
n
A_1,A_2,...A_n
A1,A2,...An是Ω中的一组事件,若满足:
1.
A
i
,
A
j
A_i,A_j
Ai,Aj两两互质
2.
∪
i
=
1
∞
A
i
\\overset{∞}{\\underset{i=1}{∪}}A_i
i=1∪∞Ai=Ω
则称
A
1
,
A
2
,
.
.
.
A
n
A_1,A_2,...A_n
A1,A2,...An是Ω的一组划分。
全概率公式(全局操作)(化整为零,逐个击破)(由因到果)
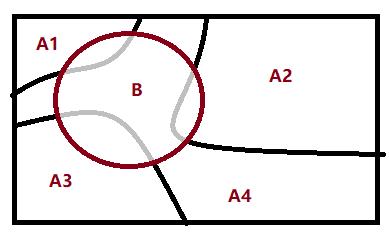
设B是Ω中一个事件,
A
1
,
A
2
,
.
.
.
A
n
A_1,A_2,...A_n
A1,A2,...An是一个划分,且P(
A
i
A_i
Ai)>0(i=1,2,…n),则有
全概率公式:
P
(
B
)
=
P
(
A
1
)
P
(
B
∣
A
1
)
+
P
(
A
2
)
P
(
B
∣
A
2
)
+
.
.
.
+
P
(
A
n
)
P
(
B
∣
A
n
)
=
∑
i
=
1
∞
P
(
A
i
)
P
(
B
∣
A
i
)
P(B)=P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+...+P(A_n)P(B|A_n)=\\overset{∞}{\\underset{i=1}{∑}}P(A_i)P(B|A_i)
P(B)=P(A1)P(B∣A1)+P(A2)P(B∣A2)+...+P(An)P(B∣An)=i=1∑∞P(Ai)P(B∣Ai)
以上是关于条件概率全概率公式的主要内容,如果未能解决你的问题,请参考以下文章