蓝桥杯18年国赛 搭积木

Posted 2021-07-18 一只特立独行的猫

小明对搭积木非常感兴趣。他的积木都是同样大小的正立方体。
在搭积木时，小明选取 m 块积木作为地基，将他们在桌子上一字排开，中间不留空隙，并称其为第0层。
随后，小明可以在上面摆放第1层，第2层，……，最多摆放至第n层。摆放积木必须遵循三条规则

规则1：每块积木必须紧挨着放置在某一块积木的正上方，与其下一层的积木对齐；

规则2：同一层中的积木必须连续摆放，中间不能留有空隙；

规则3：小明不喜欢的位置不能放置积木。

其中，小明不喜欢的位置都被标在了图纸上。图纸共有n行，从下至上的每一行分别对应积木的第1层至第n层。每一行都有m个字符，字符可能是‘.’或‘X’，其中‘X’表示这个位置是小明不喜欢的。
现在，小明想要知道，共有多少种放置积木的方案。他找到了参加蓝桥杯的你来帮他计算这个答案。
由于这个答案可能很大，你只需要回答这个答案对1000000007(十亿零七)取模后的结果。
注意：地基上什么都不放，也算作是方案之一种。

输入格式：
数据的第一行有两个正整数n和m，表示图纸的大小。
随后n行，每行有m个字符，用来描述图纸 。每个字符只可能是‘.’或‘X’。

输出格式：
一个整数，表示答案对1000000007取模后的结果。

输入样例1：

2 3
..X
.X.

输出样例1：

4

输入样例2：

3 3
..X
.X.
...

输出样例2：

16

解题思路：

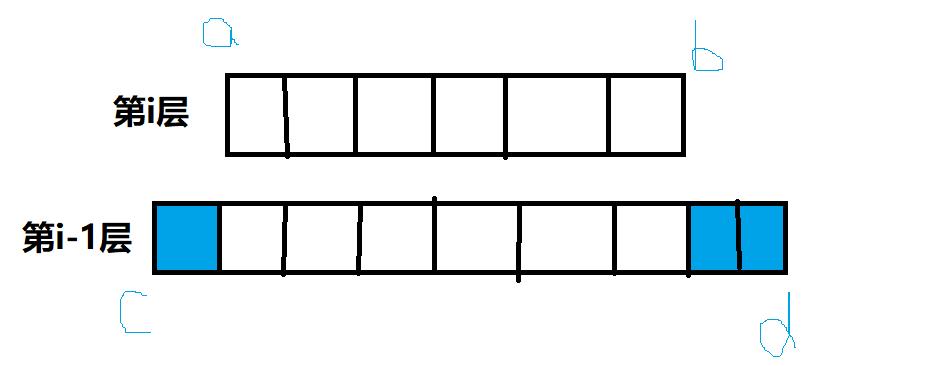
首先先推导出递推式，观察题目，可以得到递推式为：
dp[i][a][b]=$\sum _{c=1}^a\sum _{d=b}^m$p[i-1][c][d]
用代码表示即为：

for(int c=1;c<a;c++){
	for(int d=b;d<m;d++){
		dp[i][a][b]+=dp[i-1][c][d];
	}
}

意思是
在第i层的a到b长度放置积木的可能数=在i-1层的所有包含a到b的长度的积木的可能数的和。

除了单纯的判断递推式以外，还需要考虑一种特殊情况，就是积木放置的长度中存在X，即小明不想放的位置，那么就不需要进行递推，直接返回0。
判断[a,b]是否存在X，可以用前缀和来判断，节省时间。
前缀和初始化为：

s[i][j] = s[i][j-1] + (temp=='X');

推导出递推式以后可以很容易的写出代码：

#include<iostream>

using namespace std;

const int N = 30;
int n, m;
int dp[30][30][30];
int s[30][30];
int cnt=1;

int main() {
	cin >> n >> m;
	getchar();
	for (int i = n; i >0; i--) {//初始化前缀和
		for (int j = 1; j <= m; j++) {
			char temp = getchar();
			s[i][j] = s[i][j-1] + (temp=='X');
		}
		getchar();
	}
	dp[0][1][m]=1;//第0层，长度从1到m的积木有一种可能
	for (int i = 1; i <=n; i++) {//第i层
		for (int a = 1; a <= m; a++) {
			for (int b = a; b <= m; b++) {
				if (s[i][b] - s[i][a - 1] != 0) {//a到b区间存在X
					dp[i][a][b] = 0;
					continue;
				}
				for (int c = 1; c <= a; c++) {
					for (int d = b; d <= m; d++) {
						dp[i][a][b] += dp[i - 1][c][d];
					}
				}
				cnt += dp[i][a][b];//记录数量
			}
		}
	}
	cout << cnt;
	return 0;
}

优化

但是仔细一想，五个for循环无法通过最后50%的测试点，所以需要进行优化，观察最内层的两个c，d的for循环可知，有如下图像：

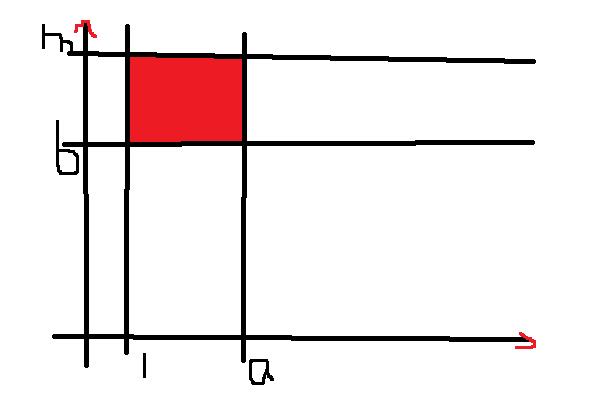
实际上最内层的两个循环就是在求第i-1层的红色区域面积。
那我们再利用二维的前缀和进行存储，那就可以优化掉两个循环，从而使时间复杂度降低，通过最后的测试点。

#include<iostream>

using namespace std;

const int N = 30;
const int mod = 1e9 + 7;
int n, m;
int dp[30][30][30];
int s[30][30];//用来判断是否存在X
int sum[30][30];//指的是左下角所有dp[i][][]的和
int cnt=1;

void get_fixsum(int i) {
	//更新第i层的前缀和数组
	for (int a = 1; a <= m; a++) {
		for (int b = 1; b <= m; b++) {
			sum[a][b] =(sum[a][b-1]+sum[a-1][b]-sum[a-1][b-1]+ dp[i][a][b])%mod;
		}
	}
}

int main() {
	cin >> n >> m;
	getchar();
	for (int i = n; i >0; i--) {
		for (int j = 1; j <= m; j++) {
			char temp = getchar();
			s[i][j] = s[i][j-1] + (temp=='X');
		}
		getchar();
	}
	dp[0][1][m]=1;//第0层，长度从1到m的积木有一种可能
	get_fixsum(0);
	for (int i = 1; i <=n; i++) {//层数
		for (int a = 1; a <= m; a++) {
			for (int b = a; b <= m; b++) {
				if (s[i][b] - s[i][a - 1] != 0) {//a到b区间存在X
					dp[i][a][b] = 0;
					continue;
				}
				dp[i][a][b] = (sum[a][m] - sum[0][m] - sum[a][b-1] + sum[0][b-1])%mod;
				cnt =(cnt+ dp[i][a][b])%mod;
			}
		}
		get_fixsum(i);
	}
	cout << (cnt+mod)%mod;//防止出现负数
	return 0;
}

我感觉挺难的，反正第一次参加国赛，重在参与嘛（佛系青年的内心独白）。