中兴2021面试题——序列最大收益(动态规划)

Posted 2021-07-18 卷王2048

序列最大收益

• 题目
• 提交记录
• 讨论
• 题解
• 视频讲解

给定一个长度为 mm 的整数序列 a1,a2,…,am。

序列中每个元素的值ai 均满足 1≤ai≤n。

当一个值为 ii 的元素和一个值为 j的元素相邻时，可以产生的收益为wi,j。

现在，我们可以从序列中删除最多 kk 个元素，删除一些元素后，原本不相邻的元素可能会变得相邻。

序列的收益和为所有相邻元素对产生的收益之和，例如一个长度为 3 的整数序列 1,3,2 的收益和为 w1,3+w3,2。

请问，通过利用删除操作，能够得到的序列的最大收益和是多少？

输入格式

第一行包含三个整数 n,k,m。

第二行包含 mm 个整数 a1,a2,…,am。

接下来 nn 行，每行包含 nn 个整数，其中第 i行第j 列的数表示 wi,j。

输出格式

输出序列的最大收益和。

数据范围

对于30% 的数据，1≤n,k,m≤20。
对于 100% 的数据，1≤n,k,m≤200，0≤wi,j≤107，1≤ai≤n1≤ai≤n。
数据保证 wi,j=wj,iwi,j=wj,i，wi,i=0wi,i=0。

输入样例：

4 1 3
1 4 2
0 3 0 1
3 0 0 0
0 0 0 0
1 0 0 0

输出样例：

3

样例解释

初始序列收益和为 w1,4+w4,2=1+0=1。

删除中间的4后，序列1,2 的收益和为 w1,2=3。

思路

最长上升子序列问题的变形

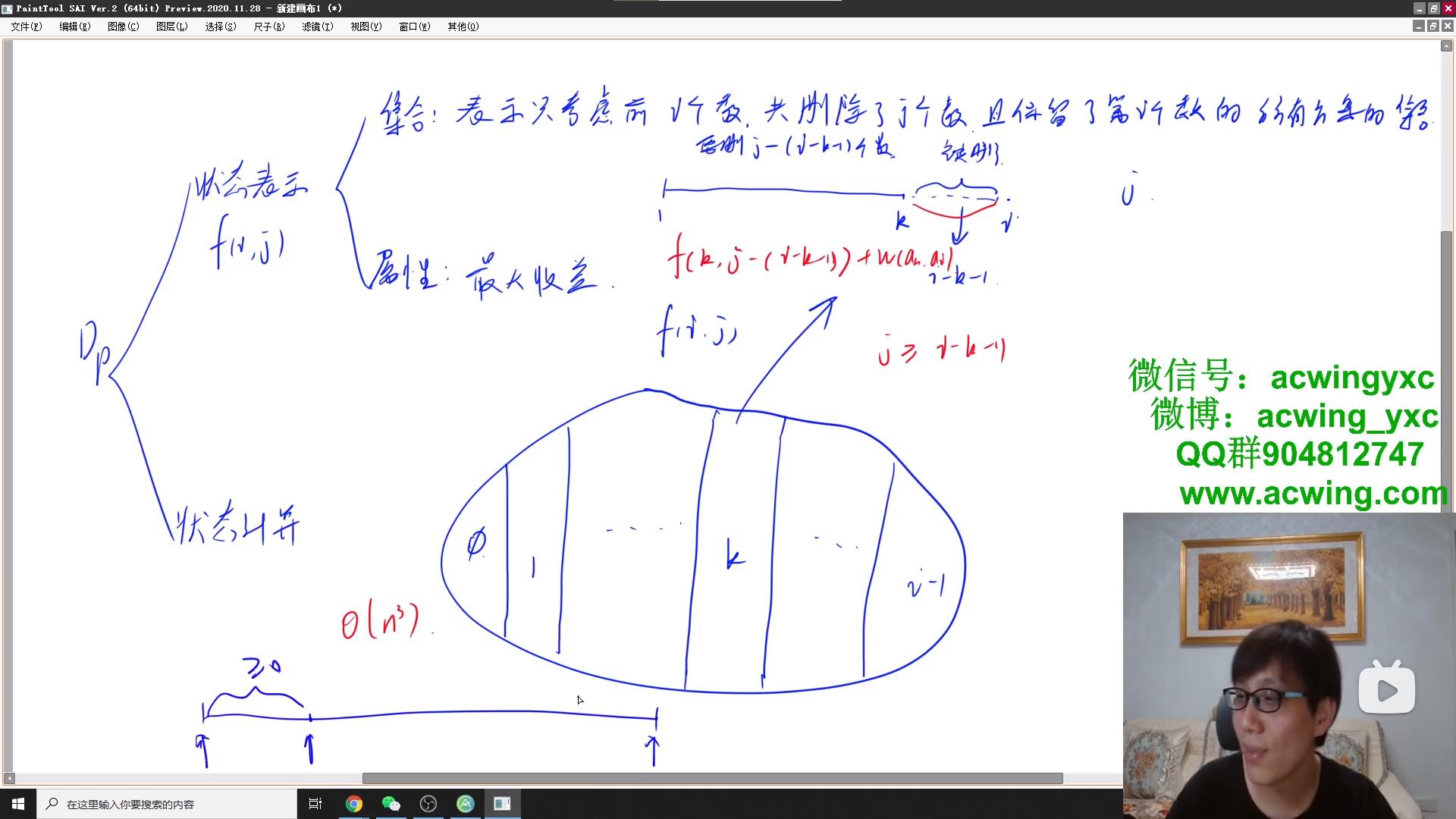
题解

import java.util.Scanner;

/**
 * @see 动态规划 https://www.acwing.com/problem/content/3502/
 */
public class Main {
    static int N = 210;
    static int m, n, k;
    static int[] arr = new int[N];
    static int[][] worth = new int[N][N];
    static int[][] dp = new int[N][N];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        k = sc.nextInt();
        m = sc.nextInt();
        for (int i = 1; i <= m; i++) {
            arr[i] = sc.nextInt();

        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                worth[i][j] = sc.nextInt();
            }
        }
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                dp[i][j] = Integer.MIN_VALUE;
            }
        }
        //集合：表示以原数组的第i个元素结尾，删除了j个数
        //属性：max
        //划分：倒数第二个数是原数组的第几个数
        //考虑在倒数第二个数与倒数第一个数之间，被删去了i-k-1个数，那么在倒数第二个数之前，被删了j-(i-k-1)个数
        //因为最后两个数已经确定，要使得前k个数的收益最大
        dp[1][0] = 0;
        for (int i = 2; i <= m; i++) {
            for (int j = 0; j <= k; j++) {
                for (int u = 1; u < i; u++) {
                    if (j >= i - u - 1) {
                        //最后两个数是原数组中第u和第i个数
                        dp[i][j] = Math.max(dp[i][j], dp[u][j - (i - u - 1)] + worth[arr[u]][arr[i]]);

                    }
                }
            }
        }
        int res = 0;
        for (int i = 0; i <= k; i++) {
            res = Math.max(res, dp[m][i]);
        }
        System.out.println(res);
    }


}