逆序问题，最大间隙问题，棋盘覆盖问题，最接近点对问题

Posted 2021-07-18 Pistachiout

一、实验目的及要求

1、从数组 seq 中找出和为 s 的数值组合，有多少种可能，并打印这些组合。

（1）问题描述：求一个算法：N个数，用其中M个任意组合相加等于一个已知数X。得出这M个数是哪些数。
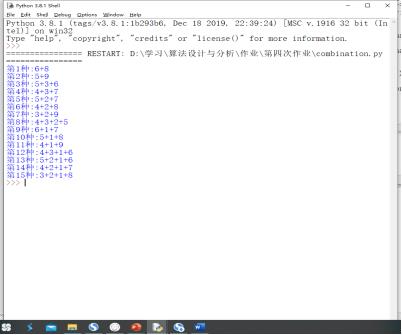
（2）问题举例：seq = [1, 2, 3, 4, 5, 6, 7, 8, 9] s = 14 则全部可能的数字组合有： 5+9, 6+8 1+4+9, 1+5+8, 1+6+7, 2+3+9, 2+4+8, 2+5+7, 3+4+7, 3+5+6 1+2+5+6, 1+3+4+6, 1+2+4+7, 1+2+3+8, 2+3+4+5 共计15种。

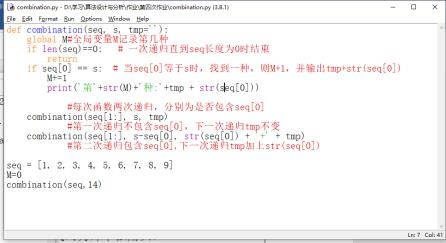
def combination(seq, s, tmp=''):
    global M#全局变量M记录第几种
    if len(seq)==0:   # 一次递归直到seq长度为0时结束
        return
    if seq[0] == s:  # 当seq[0]等于s时，找到一种，则M+1，并输出tmp+str(seq[0])
        M+=1
        print('第'+str(M)+'种:'+tmp + str(seq[0]))
        
            #每次函数两次递归，分别为是否包含seq[0]
    combination(seq[1:], s, tmp)
            #第一次递归不包含seq[0]，下一次递归tmp不变
    combination(seq[1:], s-seq[0], str(seq[0]) + '+' + tmp)
            #第二次递归包含seq[0],下一次递归tmp加上str(seq[0])

seq = [1, 2, 3, 4, 5, 6, 7, 8, 9]
M=0
combination(seq,14)

实验时，想到要求出所有可能的组合，而每组组合则需要考虑数组中每个数，则使用递归，每次减少一个数，并每次函数2次递归，第一个递归则是不包括数组第一个数，第二个递归则是包括数组第一个数，这样递归完则可以将每个数是否加上共2^len(num)种情况全考虑，将每种组合得到并输出。

2、编程实现统计逆序问题

（1）问题描述：豆瓣是一家图书、电影和音乐唱片的评价与推荐网站。这类推荐类网站会根据你对系列书籍的评价，从它的读者数据库中找出与你的评价非常类似的读者推荐给你，从而帮助你找到品味相近的朋友。假设你对五本书进行了评价，这五本书你的打分从低到高依次是[1，2，3，4，5]。另外，读者A的对这五本书的打分是[2，4，1，3，5]，而读者B的打分是[3，4，1，5，2]。那么，应该把读者A还是读者B推荐给你呢? 豆瓣也许会把读者A推荐给你，因为相比较于读者B，读者A与你的口味更为相投。那怎么来量化推荐的准则呢?这可以通过计算一个称为逆序量的来度量相似度。对于输入序列，如果元素的索引 i＜j，且ai＞aj，那么元素ai和aj是一对逆序。打分[1，2，3，4，5]的逆序对数为0，读者A打分[2，4，1，3，5]存在3对逆序，分别是｛2，1],[4，1]和[4，3]。读者B打分[3，4，1，5，2]的逆序数为5对，分别是[3，1]，[3，2]，[4，1],[4，2]和[5，2]。因此，如果用逆序数来度量推荐准则，那么读者A相比较于读者B与你有更为接近的品位。本问题就是计算给定序列的逆序数。
（2）算法设计：一个简单直接的算法就是对于每一个元素，计算该元素右边有几个元素比它小。例如，对于输入序列[2，4，1，3，5]，元素2的右边共有1个元素叫比它小，元素4的右边 共有2个元素[1，3]比它小。因此，以上序列共有3对逆序。

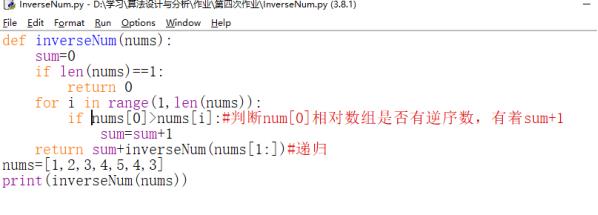
def inverseNum(nums):
    sum=0
    if len(nums)==1:
        return 0
    for i in range(1,len(nums)):
        if nums[0]>nums[i]:#判断num[0]相对数组是否有逆序数，有着sum+1
            sum=sum+1
    return sum+inverseNum(nums[1:])#递归
nums=[1,2,3,4,5,4,3]
print(inverseNum(nums))
            

算法：每个函数仅判断数组第一个值对数组是否有逆序数，然后再对数组【1：】递归

3、编程实现最大间隙问题

（1）问题描述：给定n 个实数x1 , x2 , , xn ，求这n 个数在实轴上相邻2 个数之间的最大差值。要求设计出线性时间算法。
（2）问题举例：输入数据：5
2.3，3.1，7.5，1.5，6.3
输出数据：3.2

def maxGap(nums):
    max=nums[0]
    min=nums[0]
    for i in range(0,len(nums)):#找到数组的最大值与最小值
        if nums[i]>max:
            max=nums[i]
        if nums[i]<min:
            min=nums[i]
            
    if len(nums)==2:#如果数组长度为2，返回2值之差
        return abs(nums[0]-nums[1])
    
    length=(max-min)/(len(nums)-1)#将最大值与最小值之间平均分为n-1个范围
    low,high,count={},{},{}
    for j in range(0,len(nums)-1):
        low[j]=max+1#将每个范围的左坐标赋值为数组max+1
        high[j]=min-1#将每个范围的右坐标赋值为数组min-1
        count[j]=0 #count用来记录数组中的值落在范围中的个数
        
    for i in range(0,len(nums)):#对数组中每个数遍历，找到每个数应该在哪个范围
        index=(nums[i]-min)//length#index表示数在第index+1个范围内
        if index==len(nums)-1:
                    #当index为n-1时，表示该数为最大值，index-1,分在第index+1即第n-1个范围内
            index-=1
        if nums[i]<low[index]:
                    #low[index]最开始赋值为max+1，即第一次落在该范围内的数赋给low[index]
                    #之后落在该范围内数如果比low[index]小，即将该数赋给low[index]
            low[index]=nums[i]
        if nums[i]>high[index]:
                    #high[index]最开始赋值为min+1，即第一次落在该范围内的数赋给high[index]
                    #之后落在该范围内数如果比high[index]大，即将该数赋给high[index]
            high[index]=nums[i]
        count[index]+=1#第index+1个范围内每落入一个数，count[index]+1
        
    i=0
    maxgap=0
    for i in range(1,len(nums)-1):
            #因为除了min和max还有n-2个数，放入到n-1个范围内，必至少有一个范围内没有数放入
            #且易知没有数的范围两边的范围内的数之间的间距比在同一范围内的数的间距大
            #因此数组最大间距必是相邻范围内差距
        if count[i]==0:
            #当范围内没有放入数时，该范围最小值与最大值都设为左边的范围的最大值
            low[i]=high[i-1]
            high[i]=low[i]
        if low[i]-high[i-1]>maxgap:
            #求2个范围之间的差距，差距最大值即为数组的最大差距
            maxgap=low[i]-high[i-1]
    return maxgap
nums=[1,2,3,5,6,4,4,9]
print('最大间隙为',end='')
print(maxGap(nums))

刚开始以为可以先排序，然后再求出最大间隙，后来发现这样达到不了线性时间长度的要求，于是百度发现，可以先求出最大值与最小值，然后再将其中的间隙分为len(nums)-1个范围，这样将剩下的len-2个放入到这些范围中，然后再进行最大间隙的处理便能再线性时间内解决。

4、编程实现棋盘覆盖问题

（1）问题描述：在一个2^k * 2^k个方格组成的棋盘中，恰有一个方格与其他方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。现在要用L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。
（2）算法设计：把棋盘等分成四个正方形分别是：左上、左下、右上、右下 四个子棋盘，对子棋盘进行递归求解。

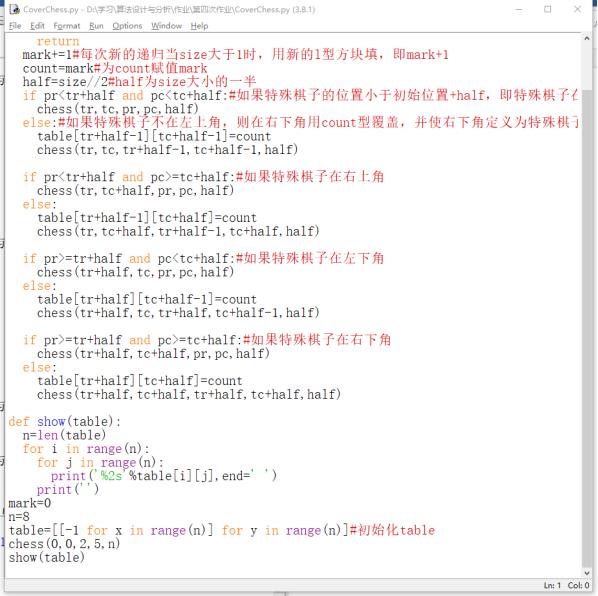
def chess(tr,tc,pr,pc,size):#tr，tc为左上角在棋盘中的位置，pr，pc为特殊棋子的位置，size为棋盘大小
  global mark
  global table
  if size==1:
    return
  mark+=1#每次新的递归当size大于1时，用新的l型方块填，即mark+1
  count=mark#为count赋值mark
  half=size//2#half为size大小的一半
  if pr<tr+half and pc<tc+half:#如果特殊棋子的位置小于初始位置+half，即特殊棋子在左上角，则在左上角棋盘递归
    chess(tr,tc,pr,pc,half)
  else:#如果特殊棋子不在左上角，则在右下角用count型覆盖，并使右下角定义为特殊棋子，再递归左上角
    table[tr+half-1][tc+half-1]=count
    chess(tr,tc,tr+half-1,tc+half-1,half)
    
  if pr<tr+half and pc>=tc+half:#如果特殊棋子在右上角
    chess(tr,tc+half,pr,pc,half)
  else:
    table[tr+half-1][tc+half]=count
    chess(tr,tc+half,tr+half-1,tc+half,half)
    
  if pr>=tr+half and pc<tc+half:#如果特殊棋子在左下角
    chess(tr+half,tc,pr,pc,half)
  else:
    table[tr+half][tc+half-1]=count
    chess(tr+half,tc,tr+half,tc+half-1,half)
    
  if pr>=tr+half and pc>=tc+half:#如果特殊棋子在右下角
    chess(tr+half,tc+half,pr,pc,half)
  else:
    table[tr+half][tc+half]=count
    chess(tr+half,tc+half,tr+half,tc+half,half)
    
def show(table):
  n=len(table)
  for i in range(n):
    for j in range(n):
      print('%2s'%table[i][j],end=' ')
    print('')
mark=0
n=8
table=[[-1 for x in range(n)] for y in range(n)]#初始化table
chess(0,0,2,5,n)
show(table)

在上课听过算法思路并看过代码后比较容易的写出程序。

5、编程实现最接近点对问题

（1）问题描述：在包含有n个点的集合S中，找出距离最近的两个点。设 p1(x1,y1)，p2(x2,y2)，……，pn(xn,yn)是平面的n个点。严格地将，最近点对可能不止一对，输出一对即可。
（2）算法设计：利用分治法思想解决此问题。将集合S分成两个子集S1和S2，最近点对将会出现三种情况：在S1中，在S2中或者最近点对分别在集合S1和S2中。利用递归法分别计算前两种情况，再与第三种情况相比较，输出三者中最小的距离。

import math
import random
minDitsance=float("inf")
def distance(x,y):#求出x，y两点间的距离
    h=math.sqrt((x[0]-y[0])**2+(x[1]-y[1])**2)
    #print(x,y)
    return h
        
def min_between(left,right,minDitsance):#找到左右各取一点的距离的最小值
    x=float("inf")
    mini=left[-1][0]-minDitsance#比较范围最小值为左边最右点的x值减去已知最小距离
    maxi=left[-1][0]+minDitsance#比较范围最大值为左边最右点的x值加上最小距离
    #print(minDitsance)
    for i in left:#取左边的点
        if (mini<i[0]<maxi):#当左边点x轴在离左边最右点一个最小距离内时
            for j in right:
                if ((mini<j[0]<maxi)and abs(i[1]-j[1])<minDitsance):
                    #当i，j的y值也在左边最右点y值一个最小距离内时求出这些点的最小距离
                    x=min(x,distance(i,j))
    return x
    
def divide(list):#递归法求最小距离
    global minDitsance
    if (len(list)==2):#列表长度为2是返回两点距离
        return distance(list[0],list[1])
    if (len(list)<2):#长度小于2返回inf
        return float("inf")
    else:
        i=int(len(list)/2)
        left = list[0:i]
        right = list[i:]#长度大于2时，将已经按x轴排序的点分割为左一半元素,右一半元素,左右分别求最近点
        s1=divide(left)#且用递归对分开的2边继续分直到找到最近点
        s2=divide(right)
        #print(left)
        #print(right)
        s3=min_between(left,right,minDitsance)
        s=min(s1,s2,s3)#最后进行比较,将左，右两边的最近距离与左右各取一点的最短距离比较取最短
        minDitsance=min(s,minDitsance)
        return minDitsance
    
def minDistancePoints(point,minDistance):#求出取最短距离的两点
    for i in point:
        for j in point:
            if distance(i,j)==minDistance and i[0]>=j[0]:
                print('最短距离的两点为',end='')
                print(i,j)
n=10
point = [(random.randint(0, 50), random.randint(0, 50)) for i in range(0, n)]
point.sort()
print(point)
minDistance=divide(point)
minDistancePoints(point,minDistance)
print(minDistance)

该题虽然在上课讲过算法，但我在编程时感受到了许多困难，最后孩子在百度上进行了很久的学习才能将程序写出来