最大子段和问题，拾捡硬币问题， 矩阵连乘问题，最短公共超序列问题，最优二分搜索树，买卖股票的最佳时机，天平秤金条问题，动态规划解最短路径问题

Posted Pistachiout

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了最大子段和问题，拾捡硬币问题， 矩阵连乘问题，最短公共超序列问题，最优二分搜索树，买卖股票的最佳时机，天平秤金条问题，动态规划解最短路径问题相关的知识，希望对你有一定的参考价值。

1、最大子段和问题

问题描述：给定长度为n的整数序列，a[1…n], 求[1,n]某个子区间[i , j]，使得a[i]+…+a[j]和最大。
示例：输入：(-2,11,-4,13,-5,2)
输出：最大子段和为20，所求子区间为[2,4]

2、拾捡硬币问题

问题描述：假如有n 个硬币排在一行，要求拾取其中的子序列，该序列的累加面值最大，但不能拾取相邻的两个硬币。
示例：输入5; 1; 2; 10; 6; 2，
输出：Max=17 （5，10，2）

3、 矩阵连乘问题

问题描述：矩阵连乘问题是通过给矩阵连乘时加括号，使得总的计算量最小。
示例：输入：[[49, 29], [29, 32], [32, 77], [77, 13], [13, 59]]，
输出：((A1(A2(A3A4)))A5)

4、最短公共超序列问题

问题描述：给出两个字符串str1和str2，返回同时以str1和str2作为子序列的最短字符串。如果答案不止一个，则可以返回满足条件的任意一个答案。如果从字符串 T 中删除一些字符（也可能不删除，并且选出的这些字符可以位于T中的任意位置），可以得到字符串 S，那么S就是T的子序列。设1<=str1.length, str2.length<=1000，str1和str2都由小写英文字母组成。
示例：输入：str1 = “abac”, str2 = “cab”
输出：“cabac”
解释：str1 = “abac” 是 “cabac” 的一个子串，因为可以删去 “cabac” 的第一个 "c"得到 “abac”。 str2 = “cab” 是 “cabac” 的一个子串，因为可以删去 “cabac” 末尾的 “ac” 得到 “cab”。最终给出的答案是满足上述属性的最短字符串。

5、对于一个n=5的关键字集合，搜索概率如下表，请构造其最优二分搜索树。

6、买卖股票的最佳时机

问题描述：给定一个数组，它的第i个元素是一支给定的股票在第i天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成k笔交易。注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
示例1：输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格=2)的时候买入，在第2天 (股票价格=4)的时候卖出，这笔交易所能获得利润=4-2=2 。
示例2：输入: [3,2,6,5,0,3], k = 2
输出: 7
解释: 在第 2 天 (股票价格=2) 的时候买入，在第3天 (股票价格=6)的时候卖出, 这笔交易所能获得利润= 6-2=4。随后，在第5天(股票价格=0)的时候买入，在第6天(股票价格=3)的时候卖出, 这笔交易所能获得利润=3-0=3

7、天平秤金条问题

问题描述：有30根金条，其中一根比其它的要重，请问用一个天平至少秤几次可以将这个重的金条找出来。
示例1：输入：[10, 10, 10, 10, 10, 11]
输出：The fake coin is coin 6 in the original list Number of weighings: 2
示例2：输入：[10, 10, 10, 10, 10, 10, 10, 10, 10,
10, 10, 10, 10, 10, 10, 10, 10, 10,
10, 10, 10, 10, 10, 10, 11, 10, 10]
输出：The fake coin is coin 25 in the original list Number of weighings: 3

8、动态规划解最短路径问题

问题描述：从某顶点出发，沿图的边到达另一顶点所经过的路径中，求各边上权值之和最小的一条路径——最短路径。
示例：输入如下图（图的输入形式自行确定）：
输出：从A到G的最短路径长度为： 18 经过的结点为： [‘B1’, ‘C2’, ‘D1’, ‘E2’, ‘F2’]
二、实验设备（环境）及要求
PC机，Windows 10

三、实验内容及结果
（包括实验过程、实验数据、实验结果及分析，实验代码另外单独附页）
1、最大子段和问题
问题描述：给定长度为n的整数序列，a[1…n], 求[1,n]某个子区间[i , j]，使得a[i]+…+a[j]和最大。
示例：输入：(-2,11,-4,13,-5,2)
输出：最大子段和为20，所求子区间为[2,4]

想法：要求最大字段和与所求区间，即从0开始相加，依次记录newsum，并用begintemp与endtemp记录区间，用maxsum保存最大的sum，并且每次新的maxsum出现时重新记录begin与end区间，当sum小于0后，证明前面sum的只会使sum变小，则从i+1重新开始相加并记录newsum，并重新记录begintemp与endtemp，每次新的maxsum出现时重新记录begin与end区间。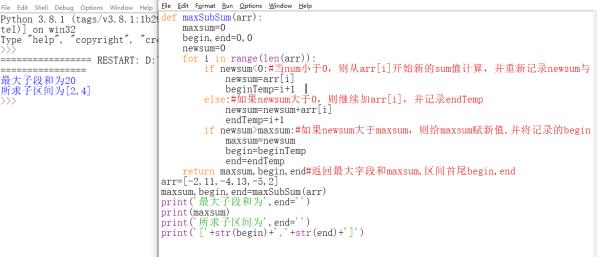在这里插入图片描述

def maxSubSum(arr):
    maxsum=0
    begin,end=0,0
    newsum=0
    for i in range(len(arr)):
        if newsum<0:#当num小于0，则从arr[i]开始新的sum值计算，并重新记录newsum与beginTemp
            newsum=arr[i]
            beginTemp=i+1  
        else:#如果newsum大于0，则继续加arr[i]，并记录endTemp
            newsum=newsum+arr[i]
            endTemp=i+1
        if newsum>maxsum:#如果newsum大于maxsum，则给maxsum赋新值,并将记录的beginTemp与endTemp赋值
            maxsum=newsum
            begin=beginTemp
            end=endTemp
    return maxsum,begin,end#返回最大字段和maxsum,区间首尾begin,end
arr=[-2,11,-4,13,-5,2]
maxsum,begin,end=maxSubSum(arr)
print('最大子段和为',end='')
print(maxsum)
print('所求子区间为',end='')
print('['+str(begin)+','+str(end)+']')

2、拾捡硬币问题
问题描述：假如有n 个硬币排在一行，要求拾取其中的子序列，该序列的累加面值最大，但不能拾取相邻的两个硬币。
示例：输入5; 1; 2; 10; 6; 2，
输出：Max=17 （5，10，2）
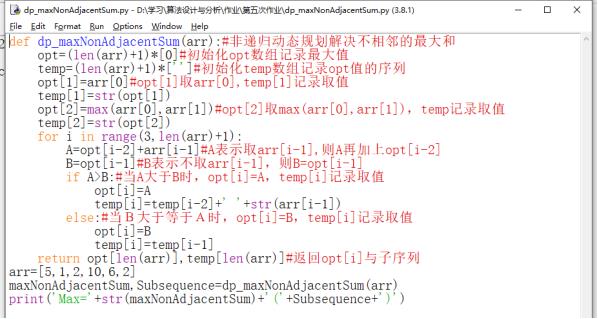
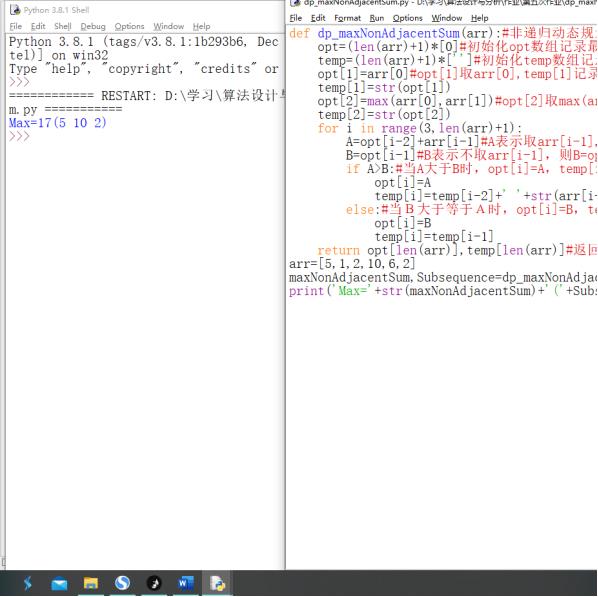
在这里插入图片描述
在这里插入图片描述

def dp_maxNonAdjacentSum(arr):#非递归动态规划解决不相邻的最大和
    opt=(len(arr)+1)*[0]#初始化opt数组记录最大值
    temp=(len(arr)+1)*['']#初始化temp数组记录opt值的序列
    opt[1]=arr[0]#opt[1]取arr[0],temp[1]记录取值
    temp[1]=str(opt[1])
    opt[2]=max(arr[0],arr[1])#opt[2]取max(arr[0],arr[1])，temp记录取值
    temp[2]=str(opt[2])
    for i in range(3,len(arr)+1):
        A=opt[i-2]+arr[i-1]#A表示取arr[i-1],则A再加上opt[i-2]
        B=opt[i-1]#B表示不取arr[i-1]，则B=opt[i-1]
        if A>B:#当A大于B时，opt[i]=A，temp[i]记录取值
            opt[i]=A
            temp[i]=temp[i-2]+' '+str(arr[i-1])
        else:#当Ｂ大于等于Ａ时，opt[i]=B，temp[i]记录取值
            opt[i]=B
            temp[i]=temp[i-1]
    return opt[len(arr)],temp[len(arr)]#返回opt[i]与子序列
arr=[5,1,2,10,6,2]
maxNonAdjacentSum,Subsequence=dp_maxNonAdjacentSum(arr)
print('Max='+str(maxNonAdjacentSum)+'('+Subsequence+')')

2.两个数组opt记录最大值，temp记录选择的硬币，opt【i】为第1个硬币到第i个硬币的最大值，有两种情况，分为选第i-1硬币时A=opt[i-2]+arr[i-1]与不选i-1硬币B=opt[i-1]，故A与B中的最大值，同时给temp记录选取的硬币，并依次遍历。

3、 矩阵连乘问题
问题描述：矩阵连乘问题是通过给矩阵连乘时加括号，使得总的计算量最小。
示例：输入：[[49, 29], [29, 32], [32, 77], [77, 13], [13, 59]]，
输出：((A1(A2(A3A4)))A5)
3.规划解决矩阵连乘，2个数组m s分别记录最少乘法次数与分割点的值，并用3次for循坏依次求出m,s[i][j],
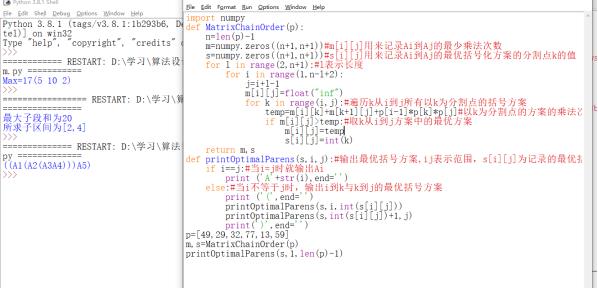
在这里插入图片描述

import numpy
def MatrixChainOrder(p):
    n=len(p)-1
    m=numpy.zeros((n+1,n+1))#m[i][j]用来记录Ai到Aj的最少乘法次数
    s=numpy.zeros((n+1,n+1))#s[i][j]用来记录Ai到Aj的最优括号化方案的分割点k的值
    for l in range(2,n+1):#l表示长度
        for i in range(1,n-l+2):
            j=i+l-1
            m[i][j]=float("inf")
            for k in range(i,j):#遍历k从i到j所有以k为分割点的括号方案
                temp=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j]#以k为分割点的方案的乘法次数计入temp
                if m[i][j]>temp:#取k从i到j方案中的最优方案
                    m[i][j]=temp
                    s[i][j]=int(k)
    return m,s
def printOptimalParens(s,i,j):#输出最优括号方案,ij表示范围，s[i][j]为记录的最优括号方案的分割点k的值
    if i==j:#当i=j时就输出Ai
        print ('A'+str(i),end='')
    else:#当i不等于j时，输出i到k与k到j的最优括号方案
        print ('(',end='')
        printOptimalParens(s,i,int(s[i][j]))
        printOptimalParens(s,int(s[i][j])+1,j)
        print(')',end='')
p=[49,29,32,77,13,59]
m,s=MatrixChainOrder(p)
printOptimalParens(s,1,len(p)-1)

4、最短公共超序列问题
问题描述：给出两个字符串str1和str2，返回同时以str1和str2作为子序列的最短字符串。如果答案不止一个，则可以返回满足条件的任意一个答案。如果从字符串 T 中删除一些字符（也可能不删除，并且选出的这些字符可以位于T中的任意位置），可以得到字符串 S，那么S就是T的子序列。设1<=str1.length, str2.length<=1000，str1和str2都由小写英文字母组成。

4.要求最短共超序列，即先用动态规划求出最长公共子序列lcs，最短公共超序列scs即为两个字符串的最长公共子序列LCS+第一个字符串除去LCS之后的序列+第二个字符串除去LCS之后的序列。
在这里插入图片描述

def shortestCommonSuperSequence(str1,str2):
    m=len(str1)
    n=len(str2)
    dp=[['']*(n+1) for i in range(m+1)]#定义dp数组记录最短公共子序列
    for i in range(1,m+1):
        for j in range(1,n+1):
            if(str1[i-1]==str2[j-1]):
                #当str1[i-1]==str2[j-1]，dp[i][j]为dp[i-1][j-1]+str1[i-1]
                #dp[i][j]记录str[1-1]与str[j-1]的最短公共子序列
                dp[i][j]=dp[i-1][j-1]+str1[i-1]
            else:
                #如果str1[i-1]与str2[j-1]不相同时
                #则令dp[i][j]取dp[i-1][j]与dp[i][j-1]中的最长子序列
                if len(dp[i-1][j]) > len(dp[i][j-1]):
                    dp[i][j]=dp[i-1][j]
                else:
                    dp[i][j]=dp[i][j-1]
                    
    lcs=dp[i][j]#lcs即为最长公共子序列等于dp[i][j]
    i,j=0,0
    scs=''
    for char in lcs:
        #最短公共超序列scs即为两个字符串的最长公共子序列LCS+第一个字符串除去LCS之后的序列+第二个字符串除去LCS之后的序列。
        while(i<m and str1[i]!=char):#i<m时若str1[i]!=charstr1[i]
            #即str1[i]不属于最长公共子序列LCS，则scs加上str1[i]
            scs+=str1[i]
            i=i+1
        while(j<n and str2[j]!=char):#j<n时若str2[j]!=char
            #即str2[j]不属于最长公共子序列LCS，则scs加上str2[j]
            scs+=str2[j]
            j=j+1
        scs+=char#scs加上循环的最长公共子序列LCS，i=i+1，j=j+1
        i=i+1
        j=j+1
    scs+=str1[i:]+str2[j:]#当加完LCS后，再加上str1[i:]与str2[j:]，即加上最长公共子序列LCS之后的部分
    return scs
str1 = "abac"
str2 = "cab"  
print(shortestCommonSuperSequence(str1,str2))

5、对于一个n=5的关键字集合，搜索概率如下表，请构造其最优二分搜索树。

.要找到最优二叉搜索树， e[i][j]用来记录包含k[i]到k[j]的最优二次搜索树的期望代价w[i][j]为k[i]到k[j]的所有子树的概率之和， e[i][j]=max（e[i][r-1]+e[r+1][j]+w[i][j]），r从1到j为根节点的位置，动态规划依次求出e[i][j],并使用flag为0，表示为根节点，flag为-1，表示k[root[i][j]]为左孩子，flag为1，表示k[root[i][j]]为右孩子，当j=i-1时，子树只包括伪关键字d[i-1]等输出最优二叉搜索树
在这里插入图片描述

def OPTIMALBST(p,q,n):
    e=[[0]*(n+2) for i in range(n+2)]#e[i][j]用来记录包含k[i]到k[j]的最优二次搜索树的期望代价
    w=[[0]*(n+2) for i in range(n+2)]#w[i][j]为k[i]到k[j]的所有子树的概率之和
    root=[[0]*(n+1) for i in range(n+1)]#root[i][j]保存根节点k[r]的下标r
    for i in range(1,n+2):#当j=i-1时，子树只包括伪关键字d[i-1]
        e[i][i-1]=q[i-1]
        w[i][i-1]=q[i-1]
    for l in range(1,n+1):#l表示长度，从1到n
        for i in range(1,n-l+2):
            j=i+l-1
            e[i][j]=float('inf')
            w[i][j]=w[i][j-1]+p[i]+p[j]
            for r in range(i,j+1):
                t=e[i][r-1]+e[r+1][j]+w[i][j]#t记录以k[r]为根节点的从k[i]到k[j]的搜索代价
                if t<e[i][j]:#取最优的二叉搜索树
                    e[i][j]=t
                    root[i][j]=r
    return e,root
def printOPTIMALBST(i,j,flag):#输出最优二叉树的结构
    if(i<=j):#当j>=i时
        if flag==0:#flag为0，表示为根节点
            print('k'+str(root[i][j])+'为根')
        elif flag==-1:#flag为-1，表示k[root[i][j]]为左孩子
            print('k'+str(root[i][j])+'为k'+str(j+1)+'的左孩子')
        else:#flag为1，表示k[root[i][j]]为右孩子
            print('k'+str(root[i][j])+'为k'+str(i-1)+'的右孩子')
        printOPTIMALBST(i,root[i][j]-1,-1)
        printOPTIMALBST(root[i][j]+1,j,1)
    elif j==i-1:#当j=i-1时，子树只包括伪关键字d[i-1]
        if flag==-1:
            print('d'+str(j)+'为k'+str(j+1)+'的左孩子')
        elif flag==1:
            print('d'+str(j)+'为k'+str(i-1)+'的右孩子')
p=[0,0.15,0.10,0.05,0.10,0.20]
q=[0.05,0.10,0.05,0.05,0.05,0.10]
n=5
e,root=OPTIMALBST(p,q,n)
print('最优二叉搜索树为')
printOPTIMALBST(1,n,0)

6、买卖股票的最佳时机
问题描述：给定一个数组，它的第i个元素是一支给定的股票在第i天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成k笔交易。注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
示例1：输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格=2)的时候买入，在第2天 (股票价格=4)的时候卖出，这笔交易所能获得利润=4-2=2 。
示例2：输入: [3,2,6,5,0,3], k = 2
输出: 7
解释: 在第 2 天 (股票价格=2) 的时候买入，在第3天 (股票价格=6)的时候卖出, 这笔交易所能获得利润= 6-2=4。随后，在第5天(股票价格=0)的时候买入，在第6天(股票价格=3)的时候卖出, 这笔交易所能获得利润=3-0=3

在这里插入代码片

要求最大利益，且用k定义买卖的次数，则只有用3维数组profit[i][j][0]表示第i天第j次交易，身上没有股票时的最大利益profit[i][j][1]表示第i天地j次交易但身上有股票时的最大利益，并且对profit[i][j][0]与profit[i][j][1]都有2种求值的方法，在第i天可以买（卖）股票或不买卖股票，且还要用j记录是第几次交易，所有第i天要求profit[i][0][0]，profit[i][0][1]，profit[i][j][0]，profit[i][j][1]（j从1到k-1），profit[i][k][0]，每种都要取2种求值方法的最大值，而最后的求解的最大值maxProfit=profit[len(prices)-1][j][0]
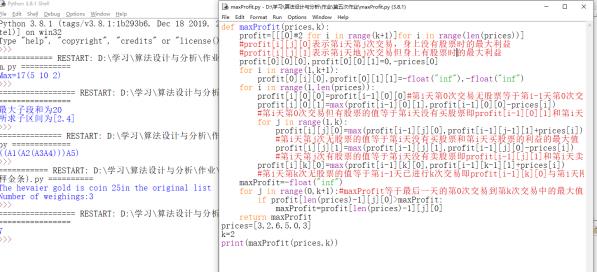
在这里插入图片描述

def maxProfit(prices,k):
    profit=[[[0]*2 for i in range(k+1)]for i in range(len(prices))]
    #profit[i][j][0]表示第i天第j次交易，身上没有股票时的最大利益
    #profit[i][j][1]表示第i天地j次交易但身上有股票时的最大利益
    profit[0][0][0],profit[0][0][1]=0,-prices[0]
    for i in range(1,k+1):
        profit[0][i][0],profit[0][1][1]=-float以上是关于最大子段和问题，拾捡硬币问题， 矩阵连乘问题，最短公共超序列问题，最优二分搜索树，买卖股票的最佳时机，天平秤金条问题，动态规划解最短路径问题的主要内容，如果未能解决你的问题，请参考以下文章
 

 最大子段和||最大子矩阵和||最大全0子矩阵||最大全0子正方形


 动态规划&数塔取数&矩阵取数&背包问题&最大子段和&正整数分组


 [POJ1050]To the Max(最大子段和)


 51Nod 1050 循环数组最大子段和 | DP


 HDU6638  Snowy Smile （线段树+二维最大子段和）


 算法笔记--最大子段和问题