栈帧，堆/栈，堆的函数使用，堆排序

Posted 2021-07-18 蚍蜉撼树谈何易

区分一下堆栈，同时给出堆的实现

• 堆/栈，栈帧，栈和队列区别
• 堆
• • 什么是堆？
  • 堆的实现--利用结构体来实现堆
  • 堆排序

堆/栈，栈帧，栈和队列区别

堆/栈：虚拟进程地址空间分段的一块内存区域的划分。指的是一块特殊的内存空间，该内存空间中保存的都是与函数调用的相关的一些信息。该空间设计的时候与数据结构中栈的特性一致。
栈帧也叫过程活动记录，是编译器用来实现过程/函数调用的一种数据结构。简言之，栈帧就是利用EBP（帧指针）寄存器访问局部变量、参数、函数返回地址手段每块独立的栈帧一般包括（1.函数的返回地址和参数）（2.临时变量：包括函数的非静态局部变量以及编译器自动生成的其他临时变量）（3.函数调用的上下文）

堆

什么是堆？

堆可以理解为一个完全二叉树的一维数组存储。

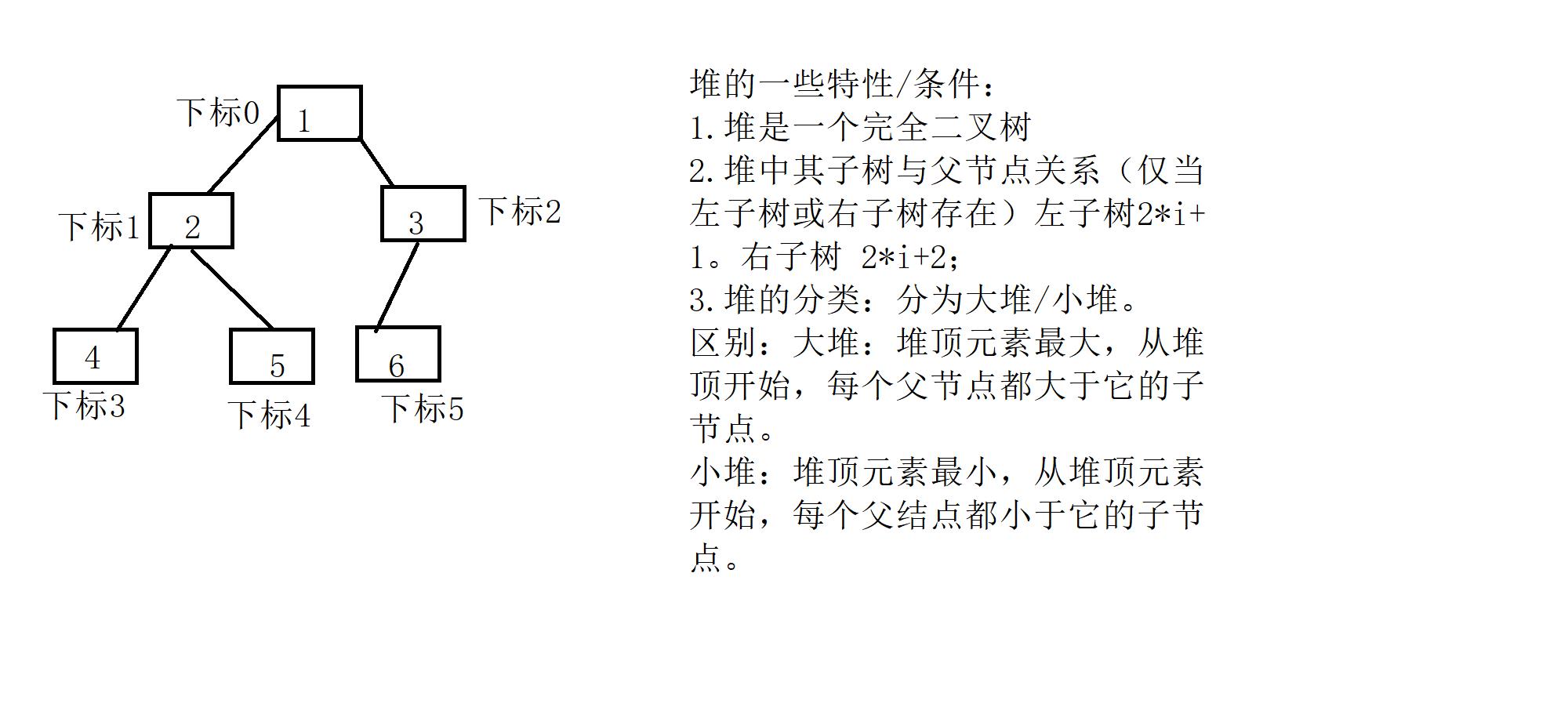
堆的实现–利用结构体来实现堆

//堆中元素的定义

typedef int datatype;
typedef int(*My_comcare)(datatype num1,datatype  num2);
typedef struct Heap
{
	datatype* val;//数组
	int capacity;//容量
	int size;//有效元素个数
	My_comcare m1;//函数接口

}Heap;

堆的初始化：

//传入的数组是 3,4,5,1,0,8 
void Heap_init(Heap* p, datatype arr[], int size, My_comcare mp)
{
	assert(p);
	p->val = (datatype*)malloc(sizeof(datatype) * size);
	if (p->val == 0)
	{
		printf("内存开辟失败\\n");
		return;
	}
	p->size = size;
	p->capacity = size;
	memcpy(p->val, arr, sizeof(datatype) * size);
	int root = (size - 2) / 2;
	p->m1 = mp;
	for (; root >= 0; root--)
	{
		adjust_down(p, root);//对堆中的元素进行向下调整
	}

}

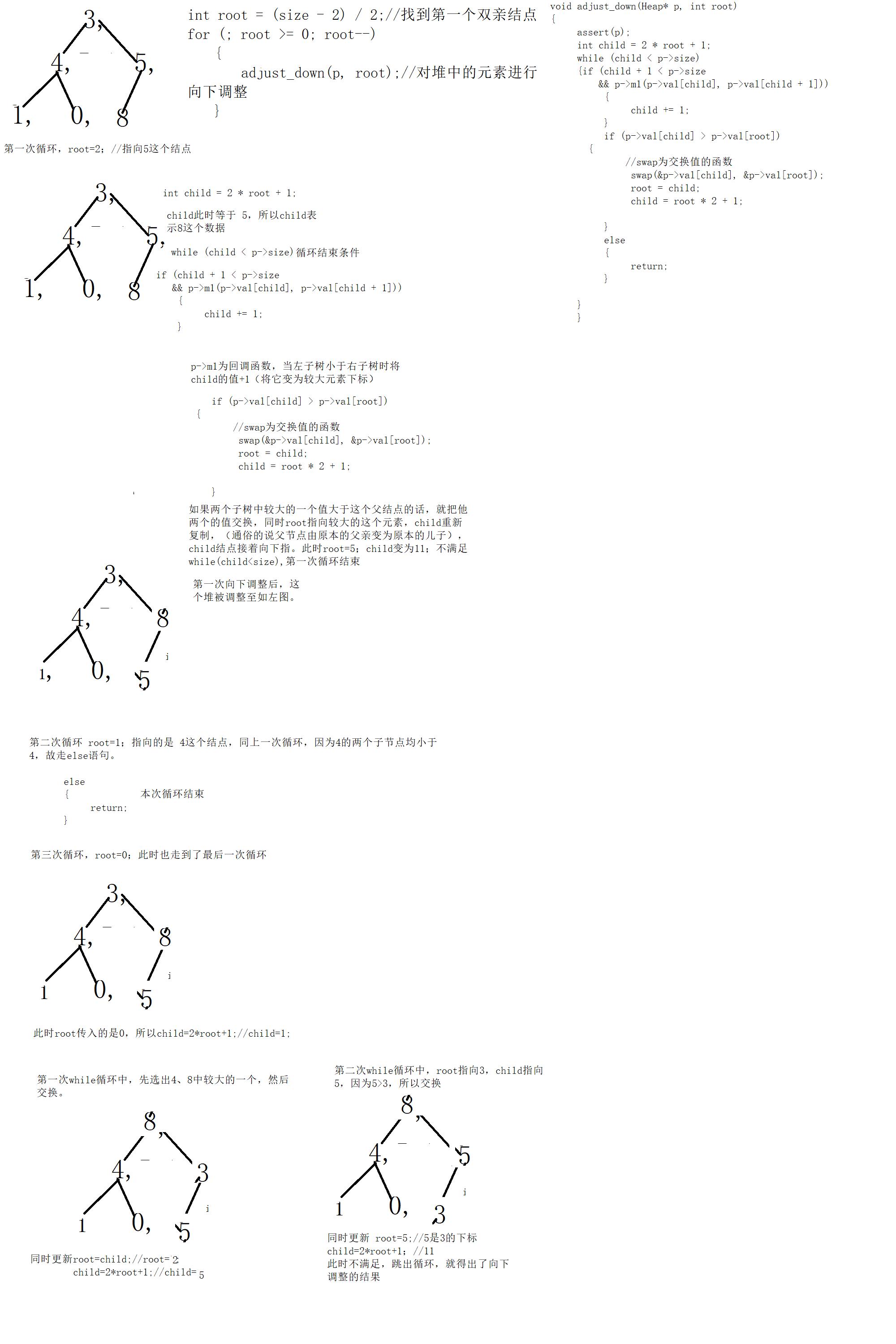
对堆中的元素向下调整

void adjust_down(Heap* p, int root)
{
	assert(p);
	int child = 2 * root + 1;
	while (child < p->size)
	{
		if (child + 1 < p->size && p->m1(p->val[child], p->val[child + 1]))
		{
			child += 1;
		}
		if (p->val[child] > p->val[root])
		{
			swap(&p->val[child], &p->val[root]);
			root = child;
			child = root * 2 + 1;
			
		}
		else
		{
			return;
		}

	}
}

调整示意图：：

大小堆外置接口

//接口一，小堆接口
int Big_heap(datatype num1, datatype num2)
{
	return num1 > num2;
}
//接口二，大堆接口
int Small_heap(datatype num1, datatype num2)
{
	return num1 < num2;
}

堆的删除元素，一般是栈顶

void Heap_delete(Heap* p)
{
	assert(p&&p->val!=NULL);
	//先交换元素
	swap(&p->val[0], &p->val[p->size - 1]);
	//将元素个数减一
	p->size--;
	int root = (p->size - 1) / 2;
	//然后重新利用向下调整方法
	for (; root >= 0; root--)
	{
		adjust_down(p, root);//方法同上方图片
	}
}

堆内存的重开辟，为了插入元素

void check(Heap* p)
{
	assert(p);
	if (p->size == p->capacity)
	{
		p->val = (datatype*)realloc(p->val, sizeof(datatype) * p->capacity * 2);
		if (p->val == NULL)
		{
			return;
		}
		p->capacity *= 2;

	}
}

堆的向上调整

void adjust_up(Heap* p, int root)
{
	assert(p);
	int child = root;
	int parent = (root-1)>>1;
	while (root)
	{
		if (p->val[root] > p->val[parent])
		{
			swap(&p->val[root], &p->val[parent]);
			root = parent;
			parent = (root - 1) >> 2;
		}
		else
		{
			return;
		}
	}
}

堆的插入

void Heap_insert(Heap* p, datatype data)
{
	assert(p->val);
	check(p);//首先对空间进行检测，看是否满
	p->val[p->size++] = data;//将数据插入到数组的最后一位
	int root = p->size - 1;//获取到了新数组的最后一个有效元素
    adjust_up(p, root);
	
	
}

示例图：

判断堆是否为空

int is_empty(Heap* p)
{
	assert(p);
	return p->size == 0;
}

返回堆顶元素

//返回堆顶元素
datatype Heap_top(Heap* p)
{
	assert(p->val);
	return p->val[0];
}

获取有效元素的个数

int Heap_size(Heap* p)
{
	assert(p);
	return p->size;
}

堆的销毁

void Heap_destory(Heap* p)
{
	assert(p);
	if (p->val != NULL)
	{
		free(p->val);
		p->val = NULL;
	}
}

堆的销毁

void Heap_destory(Heap* p)
{
	assert(p);
	if (p->val != NULL)
	{
		free(p->val);
		p->val = NULL;
	}
}

测试接口

void test()
{
	int arr[] = { 3,4,5,1,0,8 };
	int len = sizeof(arr) / sizeof(arr[0]);
	Heap p;
	Heap_init(&p, arr, len, Small_heap);
	printf("堆顶元素为%d\\n", Heap_top(&p));
	printf("有效元素个数为%d\\n", Heap_size(&p));
	Heap_insert(&p, 9);
	printf("堆顶元素为%d\\n", Heap_top(&p));
	printf("有效元素个数为%d\\n", Heap_size(&p));
	Heap_delete(&p);
	/*sort_myHeap(&arr, len);
	for (int i = 0; i < len; i++)
	{
		printf("%d\\n", arr[i]);
	}*/
	printf("堆顶元素为%d\\n", Heap_top(&p));
	printf("有效元素个数为%d\\n", Heap_size(&p));
	
}

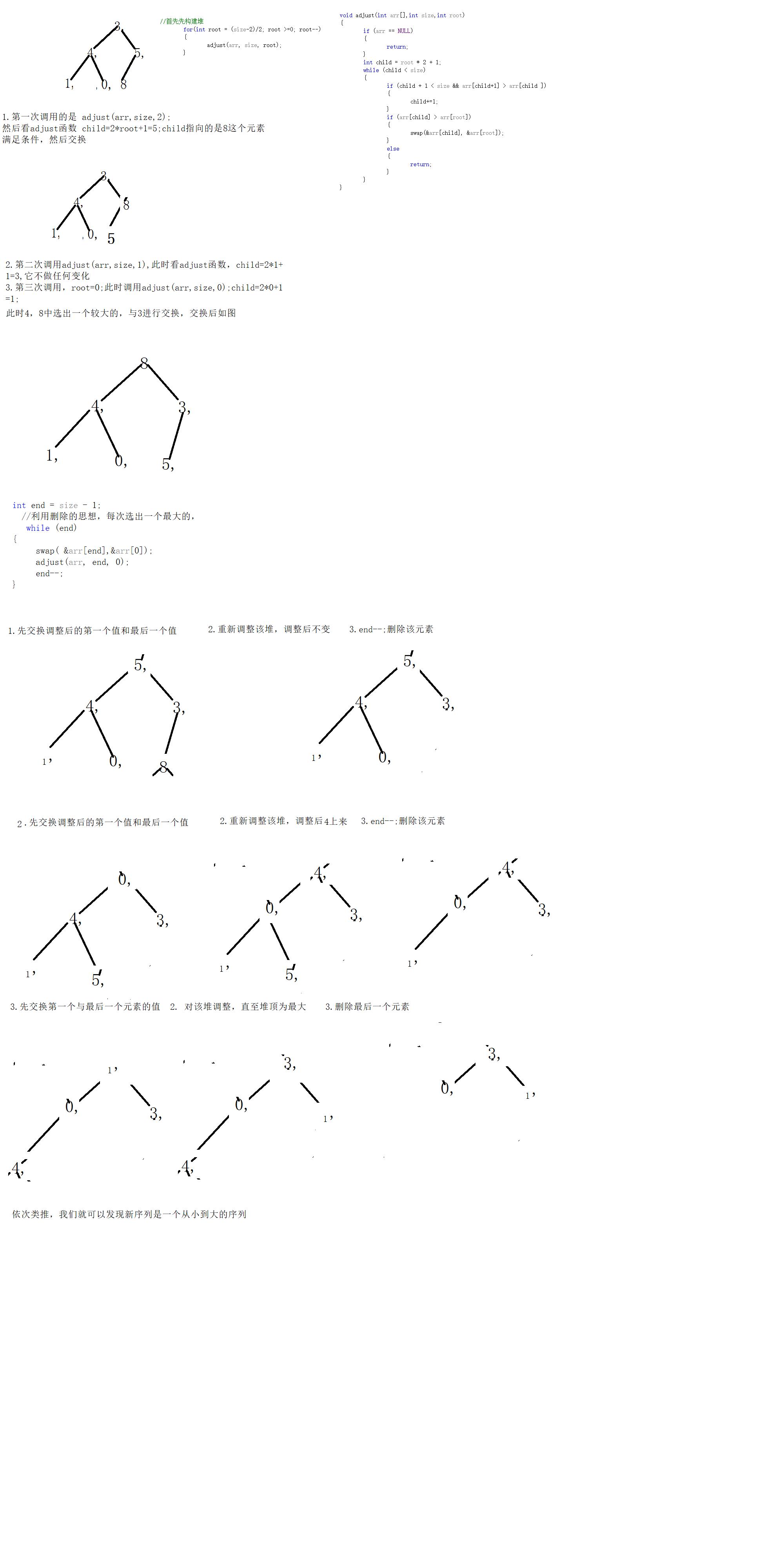
堆排序

void sort_myHeap(int arr[], int size)
{
	
	int end = size - 1;
	//首先先构建堆
	for(int root = (size-2)/2; root >=0; root--)
	{
		adjust(arr, size, root);
	}
	//利用删除思想每次选出一个最大的与它最后一个元素做交换，同时求出新堆的最大元素，将end--，这是为了让排好序的可以出去，不参与比较
	while (end)
	{
		swap( &arr[end],&arr[0]);
		adjust(arr, end, 0);
		end--;
	}

	
}

void adjust(int arr[],int size,int root)
{
	if (arr == NULL)
	{
		return;
	}
	int child = root * 2 + 1;
	while (child < size)
	{
		if (child + 1 < size && arr[child+1] > arr[child ])
		{
			child+=1;
		}
		if (arr[child] > arr[root])
		{
			swap(&arr[child], &arr[root]);
			root=child;
			child=2*root+1;
		}
		else
		{
			return;
		}
	}
}

会好起来的！！