数据结构之二叉树详解
Posted 蚍蜉撼树谈何易
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构之二叉树详解相关的知识,希望对你有一定的参考价值。
树的定义
由一个或多个(n≥0)结点组成的有限集合T,有且仅有一个结点称为根(root),当n>1时,其余的结点分为m(m≥0)个互不相交的有限集合T1,T2,…,Tm。每个集合本身又是棵树,被称作这个根的子树 。
树的结构特点
非线性结构,有一个直接前驱,但可能有多个直接后继(1:n)
树的定义具有递归性,树中还有树。
树可以为空,即节点个数为0。
若干术语
根 à 即根结点(没有前驱)
叶子 à 即终端结点(没有后继)
森林 à 指m棵不相交的树的集合(例如删除A后的子树个数)
有序树 à 结点各子树从左至右有序,不能互换(左为第一)
无序树 à 结点各子树可互换位置。
双亲 à 即上层的那个结点(直接前驱) parent
孩子 à 即下层结点的子树 (直接后继) child
兄弟 à 同一双亲下的同层结点(孩子之间互称兄弟)sibling
堂兄弟 à 即双亲位于同一层的结点(但并非同一双亲)cousin
祖先 à 即从根到该结点所经分支的所有结点
子孙 à 即该结点下层子树中的任一结点
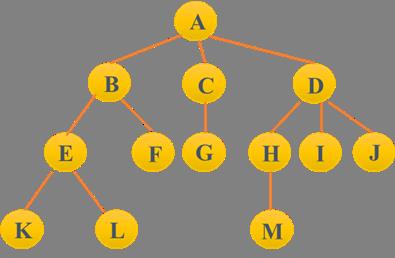
结点 à 即树的数据元素
结点的度 à 结点挂接的子树数(有几个直接后继就是几度)
结点的层次 à 从根到该结点的层数(根结点算第一层)
终端结点 à 即度为0的结点,即叶子
分支结点 à 除树根以外的结点(也称为内部结点)
树的度 à 所有结点度中的最大值(Max{各结点的度})
树的深度(或高度) à 指所有结点中最大的层数(Max{各结点的层次})
上图中的结点数= 13,树的度= 3,树的深度= 4
二叉树概念
二叉树基本概念
定义:
n(n≥0)个结点的有限集合,由一个根结点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成 。
逻辑结构:
一对二(1:2)
基本特征:
每个结点最多只有两棵子树(不存在度大于2的结点);
左子树和右子树次序不能颠倒(有序树)。
二叉树性质
性质1: 在二叉树的第i层上至多有2^(i-1)个结点(i>0)
性质2: 深度为k的二叉树至多有2^k -1个结点(k>0)(满二叉树的情况)
性质3: 对于任何一棵二叉树,若度为2的结点数有n2个,则叶子数(n0)必定为n2+1 (即n0=n2+1)
概念解释:
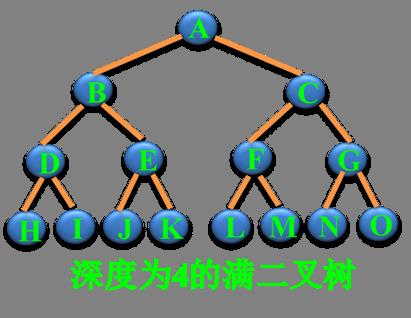
² 满二叉树
一棵深度为k 且有2^k -1个结点的二叉树。
特点:每层都“充满”了结点
² 完全二叉树
除最后一层外,每一层上的节点数均达到最大值;在最后一层上只缺少右边的若干结点。
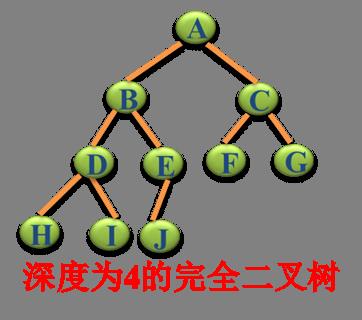
理解:k-1层与满二叉树完全相同,第k层结点尽力靠左
性质4: 具有n个结点的完全二叉树的深度必为log2 (n)+1
二叉树的遍历
遍历定义
指按某条搜索路线遍访每个结点且不重复(又称周游)。
遍历用途
它是树结构插入、删除、修改、查找和排序运算的前提,是二叉树一切运算的基础和核心。
遍历方法
牢记一种约定,对每个结点的查看都是“先左后右” 。
限定先左后右,树的遍历有三种实现方案:
DLR LDR LRD
先 (根)序遍历 中 (根)序遍历 后(根)序遍历
DLR — 先序遍历,即先根再左再右
LDR — 中序遍历,即先左再根再右
LRD — 后序遍历,即先左再右再根
二叉树的递归遍历及经典用例
首先,二叉树的递归遍历在书写上更加的简洁,可以方便我们处理一些问题,比如求叶子结点,高度,树的拷贝,查找某个元素,甚至是树的构建都可以利用递归来完成。可见递归在二叉树中的作用之大。
首先是二叉树的创建,分为数组创建(给定一个数组,构建树)和自定义树的创建(树根据自己输入元素来自行构建)
自定义树的创建
这里先给出想要创建的树的结构
先给个结构体定义
typedef int datatype;
typedef struct binary
{
datatype val;
struct binary* left;//存的是它的左子树
struct binary* right;//存的是他的右子树
}binaryTree;
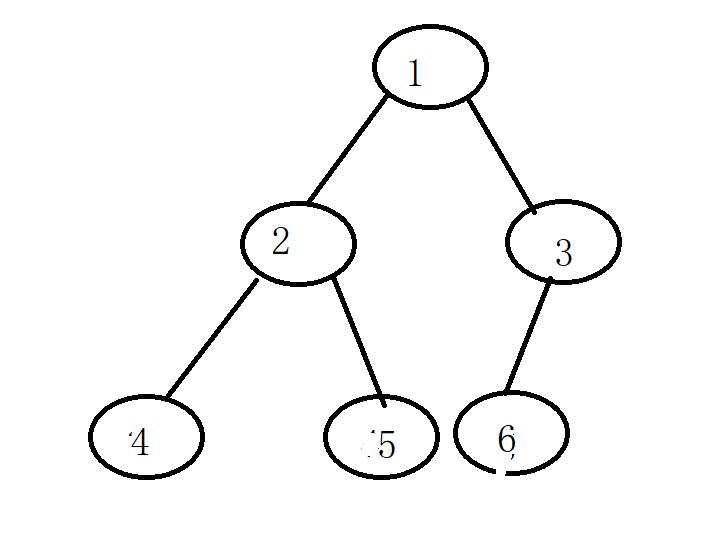
1.自行构建此二叉树
void create(binaryTree**root)
{
datatype val;
scanf("%d", &val);
if (val == -1)
{
*root = NULL;//此步是让它的结点的左子树或右子树置空操作
}
else
{
*root = (binaryTree*)malloc(sizeof(binaryTree));
if (*root == NULL)
{
printf("创建失败,返回\\n");
return;
}
(*root)->val = val;
create(&(*root)->left);
create(&(*root)->right);
}
}
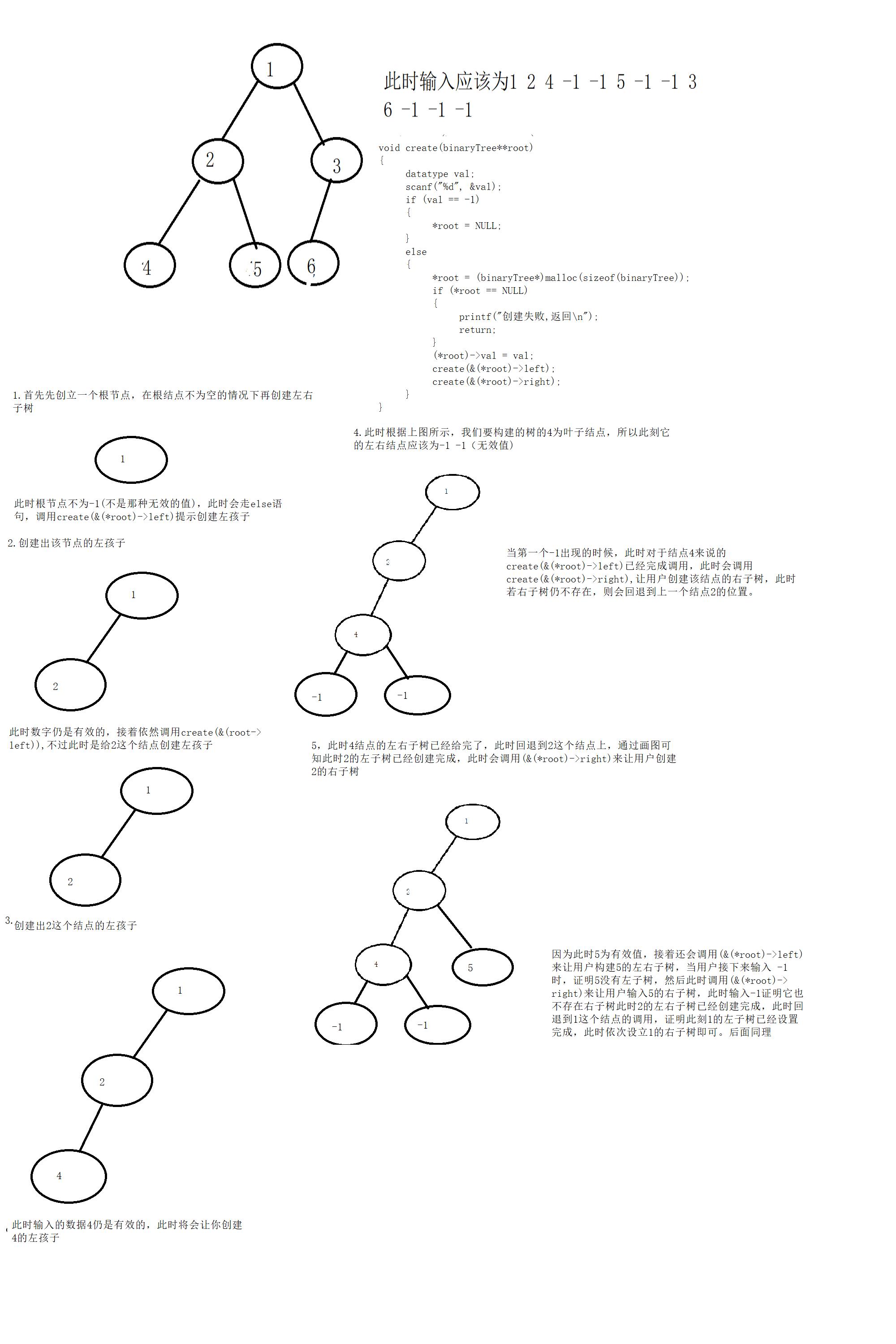
2.通过数组的方式构建此二叉树
首先给出它的内存开辟函数
binaryTree* my_malloc(datatype val)
{
binaryTree* newnode = (binaryTree*)malloc(sizeof(binaryTree));
if (NULL == newnode)
{
return NULL;
}
newnode->left = newnode->right = NULL;//在初始情况下让它的左子树与右子树指向空,这样就省去了当它左右子树为空的条件下将其左右子树置空的操作
newnode->val = val;
}
利用数组来初始化该树
binaryTree* create_v1(int arr[],int size,int invalid,int *index)//invalid 记录的是为NULL的那些结点
{
binaryTree* root = NULL;//先定义出一个根节点,让其指向空
if ((*index) < size && invalid != arr[(*index)])
{
root = my_malloc(arr[(*index)]);
++(*index);
root->left = create_v1(arr, size, invalid, index);
++(*index);
root->right = create_v1(arr, size, invalid, index);
}
return root;
}
与上面给出的自定义树方法相同,这里说明一下为什么要用 int *index来记录下标。
因为涉及到函数的出栈与入栈问题,此时若是传值调用,当一次递归完成后,此时该次递归产生的栈消耗将被释放,此时index更改后的值不会保存下来。所以此时应该传址调用。
二叉树的遍历 前序,中序,后续

void foreach(binaryTree* root)
{
if (root == NULL)
{
return;
}
//先序
printf("%d\\t", root->val);
foreach(root->left);
foreach(root->right);
中序
//foreach(root->left);
//printf("%d\\t", root->val);
//foreach(root->right);
//后序遍历
/*foreach(root->left);
foreach(root->right);
printf("%d\\t", root->val);*/
}
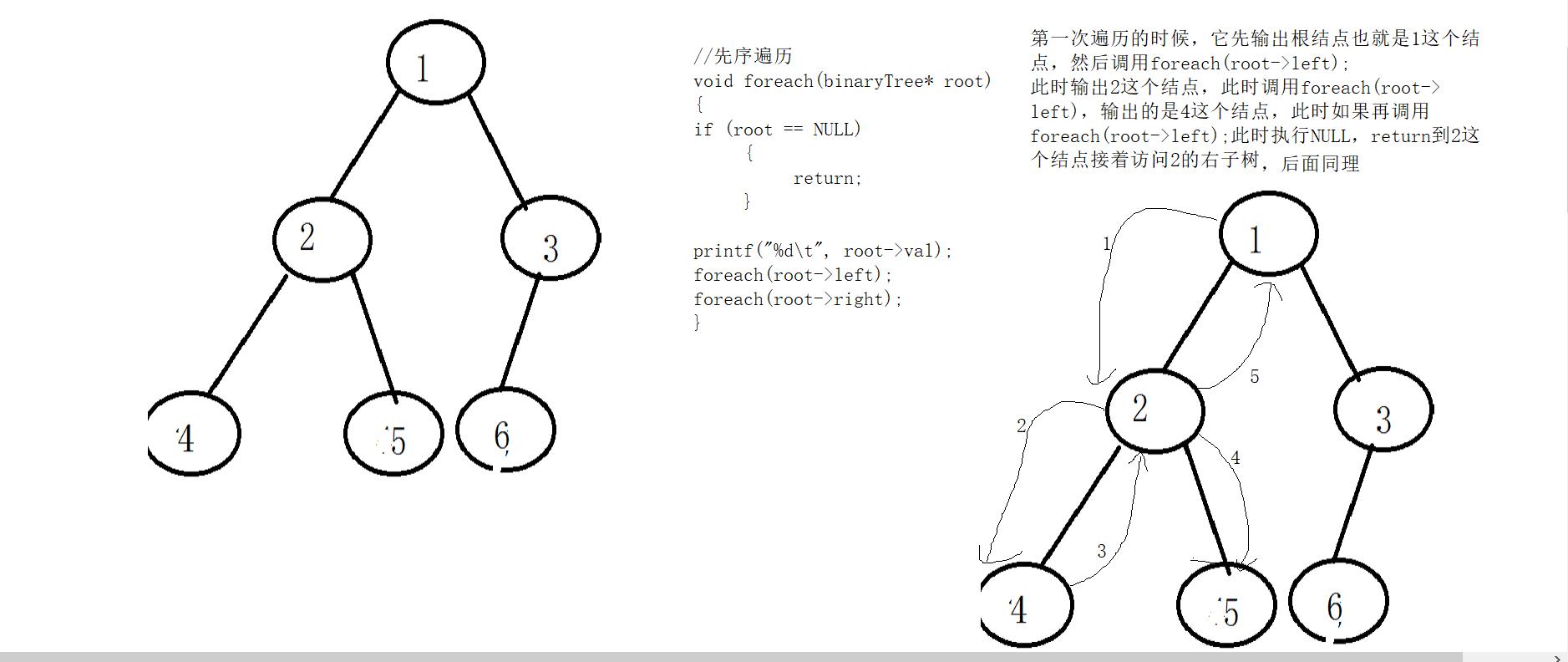
统计结点的个数(递归思想)
int Node_size(binaryTree* root)
{
if (root == NULL)
{
return 0;
}
return 1 + Node_size(root->left) + Node_size(root->right);
}
思想:当每次遍历的时候只要不为空就+1
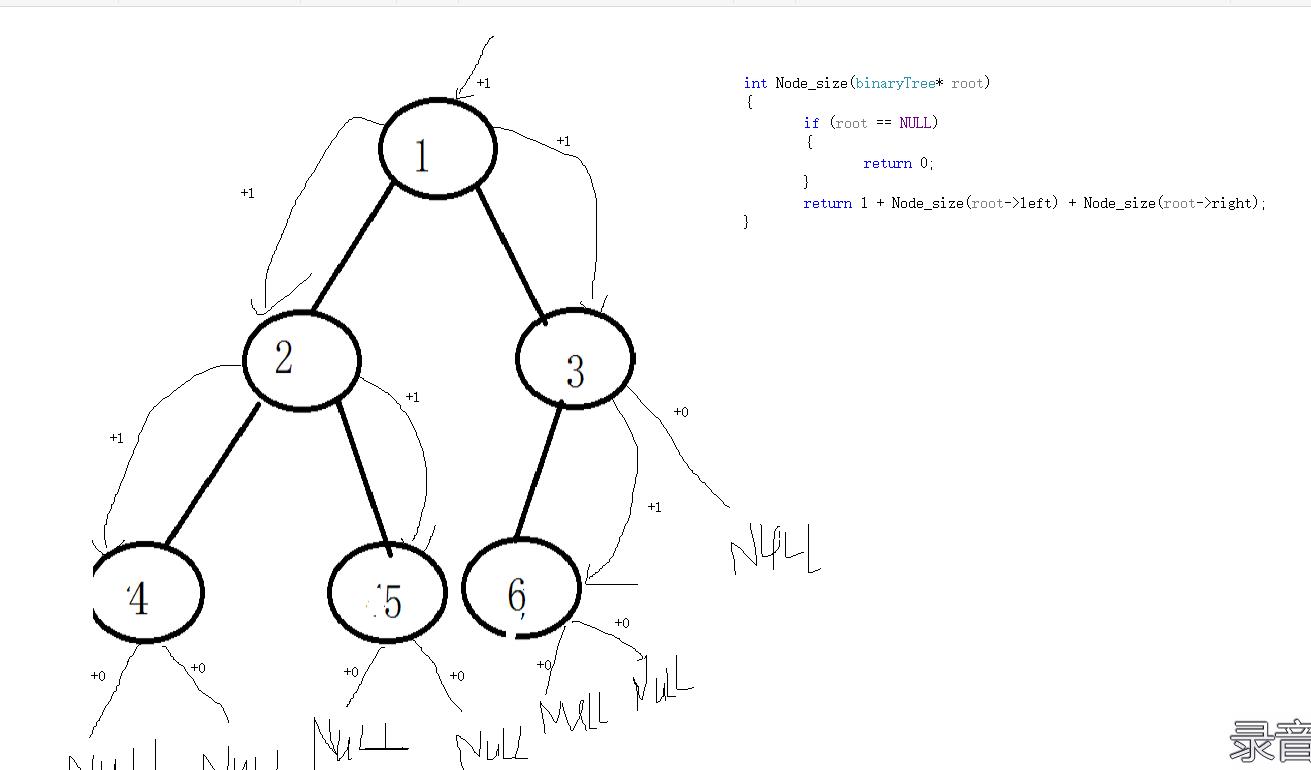
统计叶子结点
int leaf_size(binaryTree* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return leaf_size(root->left) + leaf_size(root->right);
}
思想,当一个结点的左孩子和右孩子为空时既是叶子结点,这个结点就是叶子结点。
求树的高度
int height_tree(binaryTree* root)
{
if (root == NULL)
{
return 0;
}
return height_tree(root->left) > height_tree(root->right) ? height_tree(root->left) + 1 : height_tree(root->right) + 1;
}
思想:统计出这个树的从根节点开始的左右子树的高度,选出一个比较大的数据,就是该树的高度
int level_size(binaryTree* root, int k)
{
if (root == NULL || k <= 0)
{
return 0;
}
if (k == 1)
{
return 1;
}
return level_size(root->left, k - 1) + level_size(root->right, k - 1);
}
此时求k层的结点是比较难的,所以我们此刻求的是k-1层的元素的孩子结点。就是k层的元素个数。
二叉树的拷贝
binaryTree* copy(binaryTree* root)
{
if (root == NULL)
{
return NULL;
}
binaryTree* left = copy(root->left);
binaryTree* right = copy(root->right);
binaryTree* newnode = (binaryTree*)malloc(sizeof(binaryTree));
newnode->left = left;
newnode->right = right;
return newnode;
}
树的销毁
思想:利用后续遍历的思想。
这里可不可以利用前序遍历思想、中序遍历思想做?
不可以的,因为后续遍历是先左,再右,再根,如果先释放根,就会造成子树结点没有释放完就把根释放了,后续结点就找不到了。
void destory(binaryTree* root)
{
if (root == NULL)
{
return;
}
destory(root->left);
destory(root->right);
free(root);
}
树中查找某个元素
利用遍历的思想,找到就返回。
binaryTree* find(binaryTree* root,datatype val)
{
if (root == NULL)
{
return NULL;
}
if (root->val == val)
{
return root;
}
find(root->left, val);
find(root->right, val);
}
层序遍历:
这块不能用递归了,采用队列的结构实现。
队列结构
struct binary;//引用编译器此时不知道该类型,所以此处做了个前置声明
typedef struct binary* datatype1;
typedef struct queue
{
datatype1 val;
struct queue* next;
}Qnode;
typedef struct s1
{
Qnode* front;//维护的是队列的头结点
Qnode* back;//维护的是队列的尾结点
}Queue;
队列的初始化结构
void init(Queue* p)
{
assert(p);
p->back = p->front = my_malloc(0);
}
//开辟空间
Qnode* my_malloc1(datatype1 val)
{
Qnode* newnode = (Qnode*)malloc(sizeof(Qnode));
newnode->val=val;
newnode->next = NULL;
return newnode;
}
队列的入队操作
void push_queue(Queue* p,datatype1 val)
{
assert(p);
p->back->next = my_malloc(val);
p->back = p->back->next;
}
队列的出队操作
//出队操作
void pop_queue(Queue* p)
{
Qnode* del = NULL;
assert(p);
//分两种情况,一个是删完后没有有效元素,一个是有的
if (!is_empty(p))
{
del = p->front->next;
p->front->next = del->next;
free(del);
//这里需要确定是不是出队列后就没有有效元素了
if (p->front->next == NULL)
{
p->back = p->front;//让back重新指向头结点
}
}
else
{
return;
}
}
//判断队列是否为空
bool is_empty(Queue* p)
{
return p->front == p->back;//若此时指针同一指向,则表示没有有效元素
}
队列的返回队头元素
datatype1 return_top(Queue* p)
{
assert(!is_empty(p));
return p->front->next->val;
}
队列的销毁
void destory1(Queue* p)
{
Qnode* del = p->front;
while (del)
{
p->front = del->next;
free(del);
del = p->front;
}
p->back = p->front = NULL;
}
树的层序遍历
void sequence_foreach(binaryTree* root)
{
Queue p;
if (root == NULL)
{
return;
}
init(&p);
push_queue(&p, root);
while (!is_empty(&p))
{
binaryTree* cur = return_top(&p);
printf("%d\\t", cur->val);
if (cur->left != NULL)
{
push_queue(&p, cur->left);
}
if (cur->right != NULL)
{
push_queue(&p, cur->right);
}
pop_queue(&p);
}
destory1(&p);
}
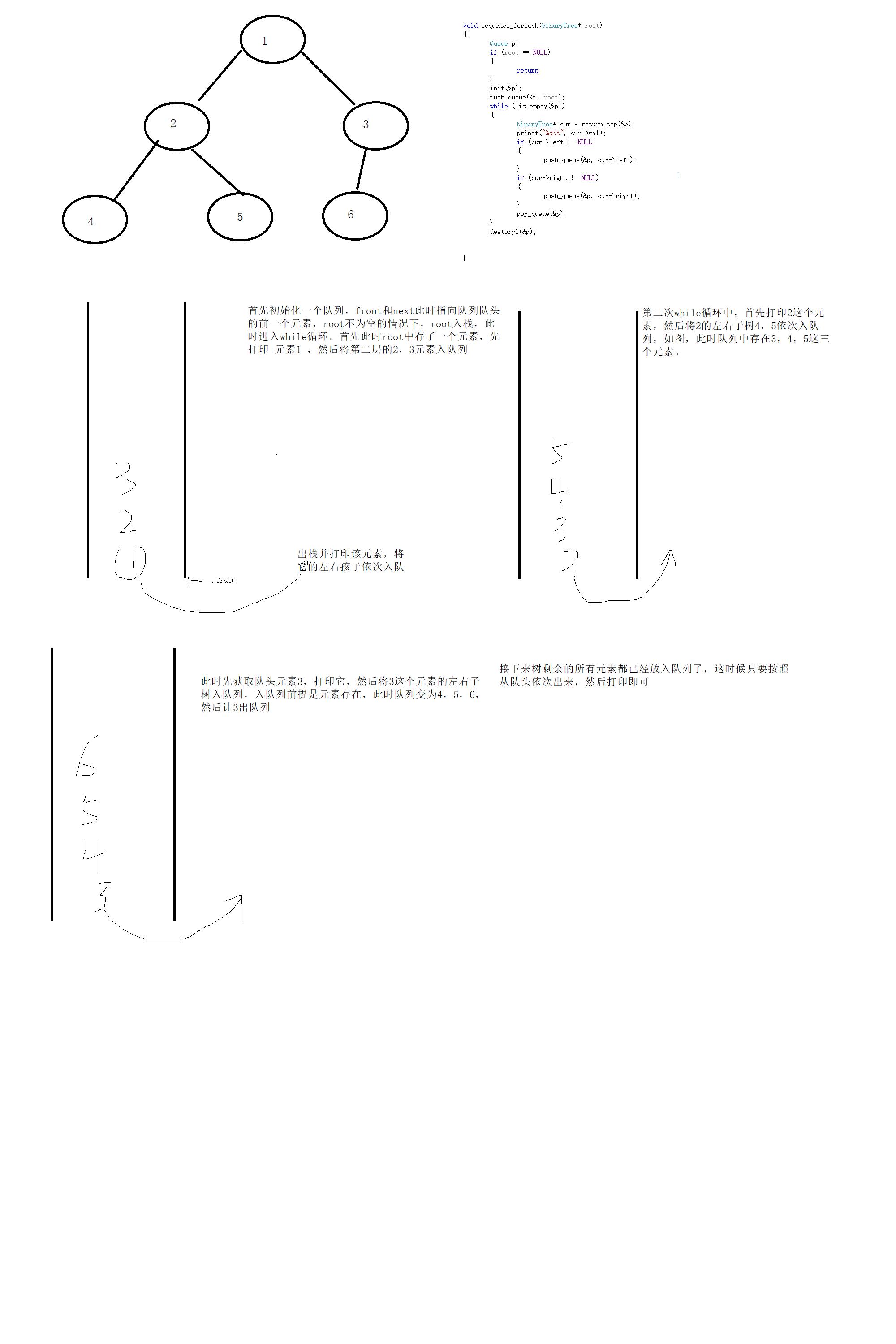
判断是不是完全二叉树
思想:还是利用层序遍历思想
1.先找到第一个不饱和的结点。
2.标志位flag两种情况会置1,左节点存在右节点不存在情况和左右均不存在情况。
3.分析,不饱和的结点必须缺的是右结点,要不就两个一起缺,同时是该层的最后一个结点,确保后续没有元素
int is_complete(binaryTree* root)
{
if (root == NULL)
{
return 1;
}
Queue p;
init(&p);
push_queue(&p, root);
while (is_empty(&p))
{
//获取队头
binaryTree* cur = return_top(&p);
int flag = 0;
if (flag == 1)
{
if (cur->left || cur->right)
{
destory1(&p);
return 0;
}
}
else
{
if (cur->left != NULL && cur->right != NULL)
{
push_queue(&p, cur->left);
push_queue(&p, cur->right);
}
else if(cur->left)
{
push_queue(&p, cur->left);
flag = 1;
}
//右子树存在的情况下左子树为空
else if(cur->right)
{
destory1(&p);
return 0;
}
else
{
flag = 1;
}
}
pop_queue(&p);
}
destory1(&p);
return 1;
}
二叉树的非递归遍历
利用栈来模拟实现,在二叉树结构体中新加一个flag标志位,为1的时候输出,为0的时候先将其左右子树入栈,然后将该结点的标志为置为1,重新入栈,这样第一次输出的值便是该树的根结点,依次类推。
首先构建栈
栈的定义
struct binary;
typedef struct binary* datatype1;
typedef struct Stack {
datatype1 *val;
int size;
int capacity;
}Stack;
栈的初始化
void init1(Stack* s)
{
assert(s);
s->val = (datatype1*)malloc(sizeof(datatype1) * 5);
s->capacity = 5;
s->size = 0;
}
栈的扩容
void extend(Stack* s)
{
if (s->size == s->capacity)
{
s->val = (datatype1 *)realloc(s->val,sizeof(datatype1)* s->capacity * 2);
if (s->val == NULL)
{
printf("内存扩容失败\\n");
return;
}
s->capacity *= 2;
}
}
入栈函数
void pushStack(Stack* s, datatype1 val)
{
assert(s);
extend(s);//目的1:测试栈满与否,目的2:为了在栈满时进行扩容
s->val[s->size++] = val;
}
判空操作
bool is_empty(Stack* s)
{
assert(s);
if (s->size != 0)
{
return false;
}
return true;
}
出栈操作
void popStack(Stack* s)
{
if (is_empty(s))
{
return;
}
else
{
s->size--;
}
}
返回栈顶元素
datatype1 return_top(Stack* s)
{
if (is_empty(s))
{
return数据结构 - 从二叉搜索树说到AVL树之二叉搜索树的操作与详解(Java)