剑指Offer - 面试题7：重构二叉树（力扣 - 105从前序与中序遍历序列构造二叉树）

Posted 2021-07-18 林夕07

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了剑指Offer - 面试题7：重构二叉树（力扣 - 105从前序与中序遍历序列构造二叉树）相关的知识，希望对你有一定的参考价值。

题目

输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如：输入前序遍历序列{1，2，4，7，3，5，6，8}和中序遍历序列{4，7，2，1，5，3，8，6}，则重建二叉树如下图。返回该二叉树的头节点。

二叉树定义如下：

struct BinaryTreeNode
{
	int m_nValue;
	BinaryTreeNode* m_pLeft;
	BinaryTreeNode* m_pRight;
};

分析

递归

首先画出先序遍历和中序遍历的结构图，由此我们可以发现只要计算出根节点在中序中的位置，所有的位置都可以表示出来
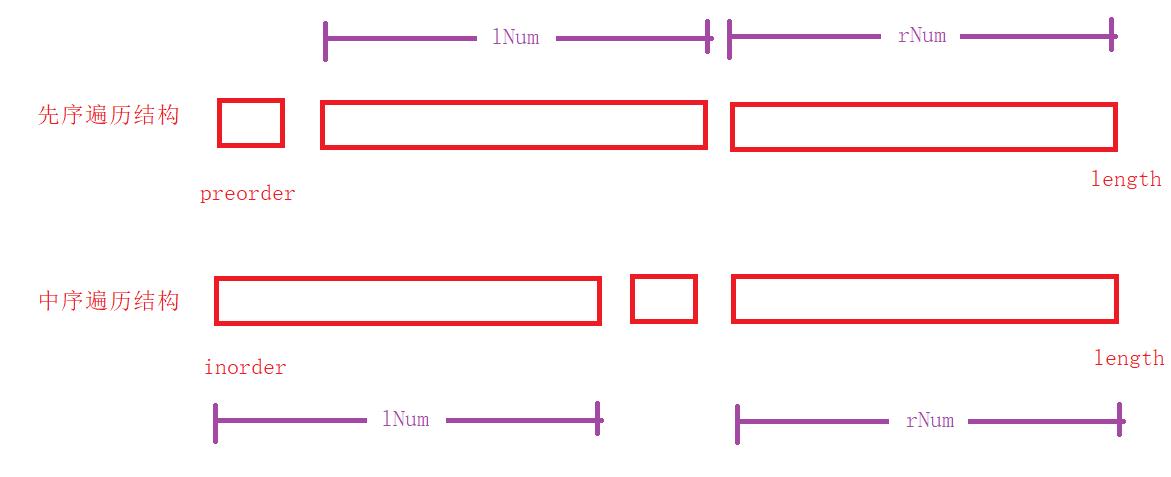
在这里插入图片描述
假设我们通过遍历得到lNum
根的左子树区域为：先序 [preorder[1] ,preorder[1+lNum] ], 中序[inorder[0],inorder[lNum]];
根的右子树区域为：先序 [preorder[1+lNum] ,preorder[length-1]], 中序[inorder[lNum+1 ],inorder[length-1]];
因为先序和中序距离一样，我们可以只拿俩数组的首地址，和子树长度即可。
C

#define _CRT_SECURE_NO_WARNINGS 1

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<math.h>
#include<assert.h>

#define MAXSIZE 100 /* 存储空间初始分配量 */

typedef int Status;		/* Status是函数的类型,其值是函数结果状态代码，如OK等 */
typedef int TElemType;  /* 树结点的数据类型，目前暂定为整型 */

struct BinaryTreeNode
{
	TElemType m_nValue;
	struct BinaryTreeNode* m_pLeft, * m_pRight;//左右孩子节点
};

void Print(TElemType n)
{
	printf("%d ", n);
}

void Preorder(BinaryTreeNode* root)//前序遍历
{
	if (NULL == root)
	{
		return;
	}

	Print(root->m_nValue);
	Preorder(root->m_pLeft);
	Preorder(root->m_pRight);
}
void Inorder(BinaryTreeNode* root)//中序输出
{
	if (root == NULL)
	{
		return;
	}

	Inorder(root->m_pLeft);
	Print(root->m_nValue);
	Inorder(root->m_pRight);
}

struct BinaryTreeNode* Construct(int* preorder, int* inorder, int length)
{
	//参数非法 以及 递归结束条件
	if (NULL == preorder || NULL == inorder || length <= 0 )
	{
		return NULL;
	}

	int i = 0;			//用于遍历查找中序数组中根的位置
	int val = 0;		//当前节点的值
	int lNum = 0;		//左子树长度
	int rNum = 0;		//右子树长度

	struct BinaryTreeNode* node = (struct BinaryTreeNode*)malloc(sizeof(struct BinaryTreeNode));
	if (NULL == node)
	{
		perror("空间申请失败！\\n");
		exit(EXIT_FAILURE);
	}

	val = preorder[0];

	//在中序数组中查找当前节点值的位置
	for (i = 0; i < length; i++)
	{
		if (val == inorder[i])
		{
			break;
		}
		lNum++;
	}
	rNum = length - lNum - 1;

	node->m_nValue = val;
	node->m_pLeft = Construct(&preorder[1], &inorder[0], lNum);
	node->m_pRight = Construct(&preorder[lNum + 1], &inorder[lNum + 1], rNum);
	
	return node;
}

int main()
{
	int pre[] = { 1,2,4,7,3,5,6,8 };
	int ino[] = { 4,7,2,1,5,3,8,6 };
	struct BinaryTreeNode * root = Construct(pre, ino, sizeof(ino) / sizeof(ino[0]));

	printf("先序输出:");
	Preorder(root);
	printf("\\n中序输出:");
	Inorder(root);

	return 0;
}

构造好二叉树后，再次输出验证。
在这里插入图片描述

C++可以用哈希表，拿空间换时间
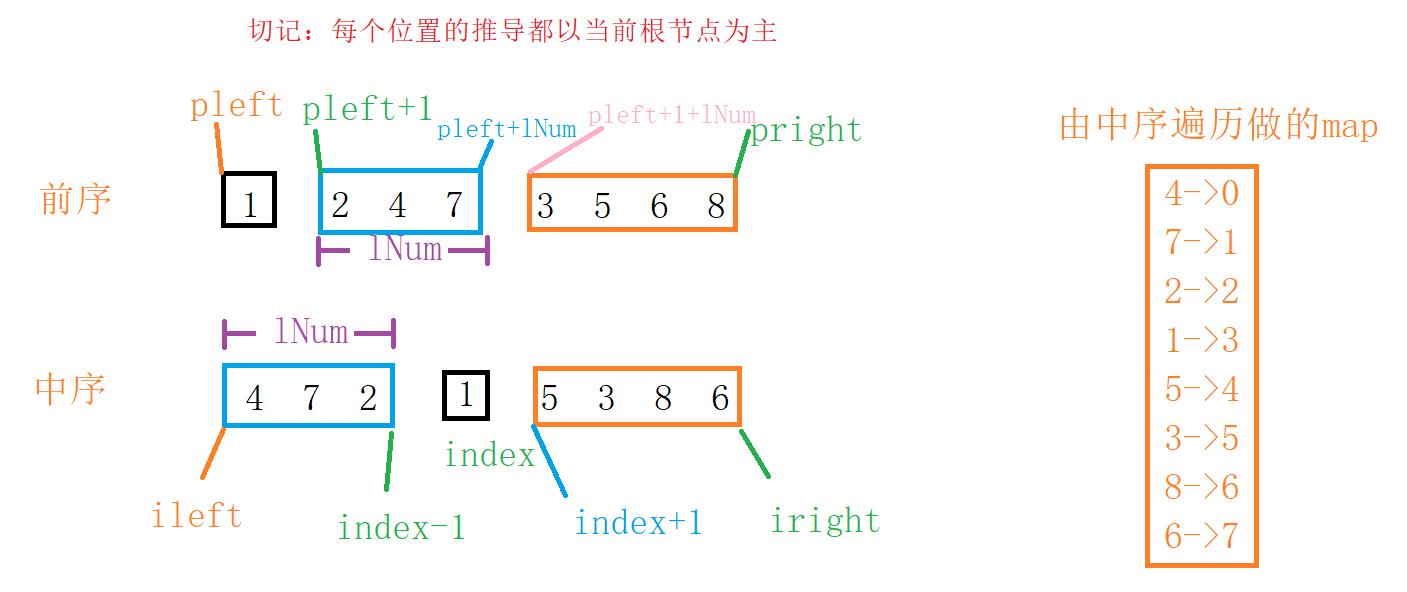
参数较多：
pleft和pright分别为前序遍历的左右闭区间。
ileft和 iright分别为中序遍历的左右闭区间。
通过前序遍历和pleft找到当前根节点。再通过哈希表找到该节点在中序遍历的位置index。进而可以求出左子树的长度lNum = index - ileft。
需要注意一点：只有index是绝对位置(按照最开始的哈希表做的)，边界下标都会收缩的。
在这里插入图片描述

include<iostream>
#include<map>

using namespace std;

#define MAXSIZE 100		/* 存储空间初始分配量 */

typedef int Status;		/* Status是函数的类型,其值是函数结果状态代码，如OK等 */
typedef int TElemType;  /* 树结点的数据类型，目前暂定为整型 */

class BinaryTreeNode
{
public:
	TElemType m_nValue;
	BinaryTreeNode* m_pLeft, * m_pRight;//左右孩子节点

public:
	BinaryTreeNode();
	BinaryTreeNode(TElemType x);
	~BinaryTreeNode();
};

BinaryTreeNode::BinaryTreeNode()
{
	m_nValue = 0;
	m_pLeft = NULL;
	m_pRight = NULL;
}

BinaryTreeNode::BinaryTreeNode(TElemType x)
{
	m_nValue = x;
	m_pLeft = NULL;
	m_pRight = NULL;
}

BinaryTreeNode::~BinaryTreeNode()
{

}

void Print(TElemType n)
{
	cout << n << " ";
}

void CreatTree(BinaryTreeNode** T)
{
	TElemType elem;

	cin >> elem;
	if (elem != 999)
	{
		*T = new BinaryTreeNode();
		if (NULL == T)
		{
			perror("空间申请失败！\\n");
			exit(EXIT_FAILURE);
		}
		(*T)->m_nValue = elem;
		CreatTree(&((*T)->m_pLeft));
		CreatTree(&((*T)->m_pRight));
	}
	else
	{
		*T = NULL;
	}
}

void Preorder(BinaryTreeNode* root)//前序遍历
{
	if (NULL == root)
	{
		return;
	}

	Print(root->m_nValue);
	Preorder(root->m_pLeft);
	Preorder(root->m_pRight);
}
void Inorder(BinaryTreeNode* root)//中序输出
{
	if (root == NULL)
	{
		return;
	}

	Inorder(root->m_pLeft);
	Print(root->m_nValue);
	Inorder(root->m_pRight);
}

BinaryTreeNode* ConstructCore(int* preorder, int* inorder, 
	int preorder_left, int preorder_right, int inorder_left, 
	int inorder_right, map<TElemType, int> m)
{
	//参数非法 以及 递归结束条件
	if (NULL == preorder || NULL == inorder || 
		preorder_left < 0 || preorder_right < preorder_left || 
		inorder_left < 0 ||inorder_right < inorder_left)
	{
		return NULL;
	}
	
	// 前序遍历中的第一个节点就是根节点preorder[preorder_index]

	// 按前序遍历preorder_left下标的值作为key找到哈希表对应的value
	// 即中序遍历中该节点的下标
	int inorder_index = m[preorder[preorder_left]];

	BinaryTreeNode* node = new BinaryTreeNode(preorder[preorder_left]);

	//左子树中的节点数目
	int lNum = inorder_index - inorder_left;

	node->m_pLeft = ConstructCore(preorder, inorder, preorder_left + 1, 
			preorder_left + lNum, inorder_left, inorder_index - 1, m);

	node->m_pRight = ConstructCore(preorder, inorder, preorder_left + 1 + lNum,
		preorder_right, 1 + inorder_index, inorder_right, m);

	return node;
}

BinaryTreeNode* Construct(int* preorder, int* inorder, int length)
{
	//参数非法
	if (NULL == preorder || NULL == inorder || length <= 0)
	{
		return NULL;
	}

	map<TElemType, int> m;
	int i = 0;
	for (i = 0; i < length; i++)
	{
		m.insert(make_pair(inorder[i], i));
	}

	return ConstructCore(preorder, inorder, 0, length - 1, 0, length - 1 , m);
}


int main()
{
	int pre[] = { 1,2,4,7,3,5,6,8 };
	int ino[] = { 4,7,2,1,5,3,8,6 };

	BinaryTreeNode* root = Construct(pre, ino, sizeof(ino) / sizeof(ino[0]));

	cout << "先序遍历:";
	Preorder(root);
	cout << endl << "中序遍历：";
	Inorder(root);

	return 0;
}

在这里插入图片描述

迭代

我们可以用一个栈来保存每次遍历的节点。先把根节点preorder[0]放入，然后遍历先序数组，从下标1开始，因为根节点提前创建。再定义一个index用来指向中序数组

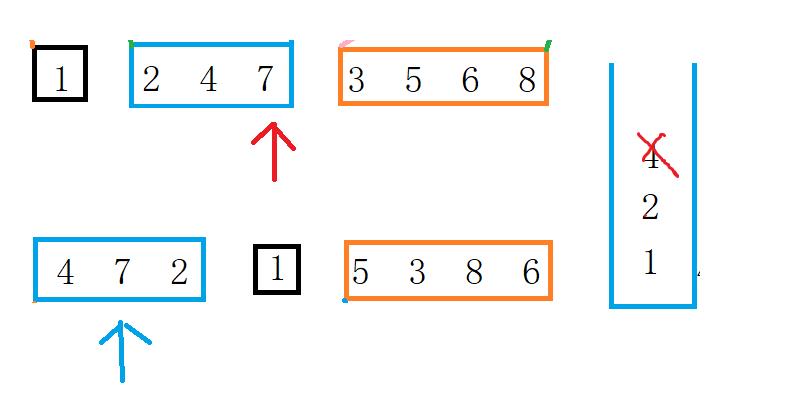
若发现栈顶指针指向的值不等于中序指针指向的值,那么说明,先序指向的值为前一个节点的左儿子。如下图

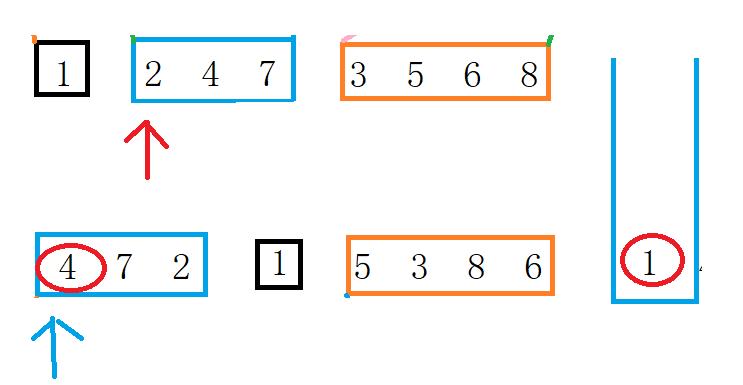
在这里插入图片描述

若发现栈顶指针指向的值等于中序指针指向的值。那么说明左儿子已经完了。那么我们需要更新中序指针。只要栈不空且栈中的值等于当前中序指针指向的值。就一直循环。

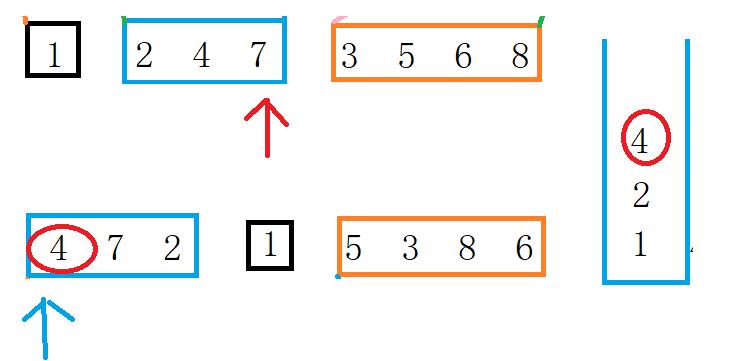
当不相等时，就说明接下来的值就是前一个节点的右儿子。所以我们在跟新中序指针时，还需要更新保存栈中的栈顶指针。见下图

在这里插入图片描述

C++

#include<iostream>
#include<stack>

using namespace std;

#define MAXSIZE 100		/* 存储空间初始分配量 */

typedef int Status;		/* Status是函数的类型,其值是函数结果状态代码，如OK等 */
typedef int TElemType;  /* 树结点的数据类型，目前暂定为整型 */

class BinaryTreeNode
{
public:
	TElemType m_nValue;
	BinaryTreeNode* m_pLeft, * m_pRight;//左右孩子节点

public:
	BinaryTreeNode();
	BinaryTreeNode(TElemType x);
	~BinaryTreeNode();
};

BinaryTreeNode::BinaryTreeNode()
{
	m_nValue = 0;
	m_pLeft = NULL;
	m_pRight = NULL;
}

BinaryTreeNode::BinaryTreeNode(TElemType x)
{
	m_nValue = x;
	m_pLeft = NULL;
	m_pRight = NULL;
}

BinaryTreeNode::~BinaryTreeNode()
{

}

void Print(TElemType n)
{
	cout << n << " ";
}

void CreatTree(BinaryTreeNode** T)
{
	TElemType elem;

	cin >> elem;
	if (elem != 999)
	{
		*T = new BinaryTreeNode();
		if (NULL == T)
		{
			perror("空间申请失败！\\n");
			exit(EXIT_FAILURE);
		}
		(*T)->m_nValue = elem;
		CreatTree(&((*T)->m_pLeft));
		CreatTree(&((*T)->m_pRight));
	}
	else
	{
		*T = NULL;
	}
}

void Preorder(BinaryTreeNode* root)//前序遍历
{
	if (NULL == root)
	{
		return;
	}

	Print(root->m_nValue);
	Preorder(root->m_pLeft);
	Preorder(root->m_pRight);
}
void Inorder(BinaryTreeNode* root)//中序输出
{
	if (root == NULL)
	{
		return;
	}

	Inorder(root->m_pLeft);
	Print(root->m_nValue);
	Inorder(root->m_pRight);
}


BinaryTreeNode* Construct(int* preorder, int* inorder, int length)
{
	if (preorder == NULL || inorder == NULL || length <= 0)
	{
		return 0;
	}

	stack<BinaryTreeNode*> s;
	BinaryTreeNode* root = new BinaryTreeNode(preorder[0]);
	s.push(root);

	int inorder_index = 0;//中序遍历的指针

	for (int i = 1; i < length; i++)//每次循环连接一个节点，还需要连接length-1个。
	{
		BinaryTreeNode* node = s.top();

		if (node->m_nValue != inorder[inorder_index])//不相等，就是左儿子
		{
			node->m_pLeft = new BinaryTreeNode(preorder[i]);
			s.push(node->m_pLeft);
		}
		else
		{
			while (s.empty() != true && s.top()->m_nValue == inorder[inorder_index])
			{
				s.pop();
				node = s.top();//更新父节点
				inorder_index++;//中序遍历指针移动
			}

			//此时i和inorder_index均指向右节点。都可以使用inorder[inorder_index]
			node->m_pRight = new BinaryTreeNode(preorder[i]);
			s.push(node->m_pLeft);
		}
	}
	return root;
}

int main()
{
	int pre[] = { 1,2,4,7,3,5,6,8 };
	int ino[] = { 4,7,2,1,5,3,8,6 };

	BinaryTreeNode* root = Construct(pre, ino, sizeof(ino) / sizeof(ino[0]));

	cout << "先序遍历:";
	Preorder(root);
	cout << endl << "中序遍历：";
	Inorder(root)以上是关于剑指Offer - 面试题7：重构二叉树   （力扣 - 105从前序与中序遍历序列构造二叉树）的主要内容，如果未能解决你的问题，请参考以下文章 
 剑指Offer——面试题7：重建二叉树
 LeetCode | 面试题32 - II. 从上到下打印二叉树 II剑指OfferPython
 剑指Offer面试题27. 二叉树的镜像
 剑指offer 面试题7.重建二叉树
 剑指offer面试题27. 二叉树的镜像
 剑指offer面试题27. 二叉树的镜像

剑指Offer - 面试题7：重构二叉树 （力扣 - 105从前序与中序遍历序列构造二叉树）

题目

分析

递归

迭代

剑指Offer - 面试题7：重构二叉树（力扣 - 105从前序与中序遍历序列构造二叉树）