医学图像处理期末复习

Posted 2021-07-17 Melody袁

图像形状和纹理量化

形状和纹理是医学图像中最有代表性和诊断启示意义的两种视觉信息。

形状测度

对分割图像进行形状量化的三种不同方法：

• 区域致密度与空间矩（Compactness and spatial moments）：对一个闭合区域内全部像素进行几何与统计计算。
• 径向距离测度、链码、Fourier描述子：仅对边界像素做几何、统计或谱计算得到编码或表示闭合轮廓的机制
• 当感兴趣的结构被拉长或展宽，重要的形状信息包含在中线之中，可以用细化（Thinning）算法提取中线。基于骨架化表示可以得到量化的形状测度，例如长度、角度、曲率或方向等
  分别介绍如下：
  区域致密度：
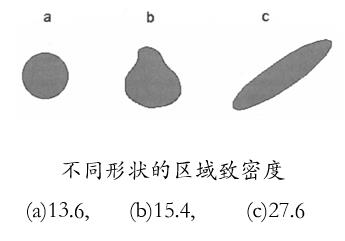
  区域致密度是常用的形状测度，用分割区域的周长P和面积A定义
  $$C=P^2/A$$
  区域致密度给出一个物体接近最平滑的形状（圆）的定量描述，这是一个无量纲的测度。由于离散数字化误差，实际的圆的C的值比理想的圆的C值稍大些。例如图(a)中的圆的C=13.6。随着图形的复杂程度增加，C值也增加。但也并非总是如此。图©中的长形椭圆从视觉上看性质并不复杂，但C=27.6，远比（b）中图形的C值大。所以使用区域致密度这个形状测度主要是因为计算简单，而且在一定限度内具有平移、旋转和尺度不变性。它的归一化表示也较常使用：

$$C^{‘}=1-4\Pi /C$$

空间矩：
考虑一个大小为M×N的图像f(i,j),它的二维p+q阶矩定义为

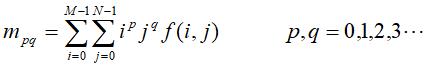
对平移不变的中心矩定义为

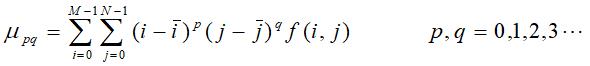
其中

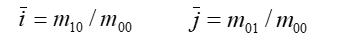
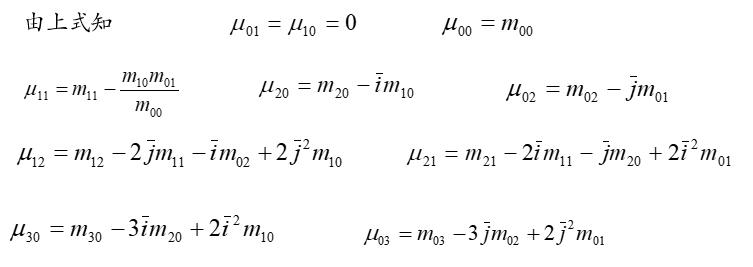
尺度不变的中心矩：
如果图像f(i,j)放大s倍，则

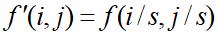
相应的矩改变为

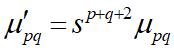
定义尺度不变的中心矩：

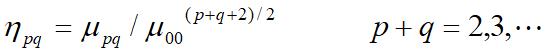
该中心矩对形状的量化与位置、大小无关。

径向距离测度：
感兴趣结构的形状也可通过分析它的边界变化情况得到量化的信息。具体的实现方法是将结构的边界先转换为1D信号，然后进行分析。
例如计算从区域中心 (Xc,yc) 到每个边界像素 (x，y) 的径向距离 ：

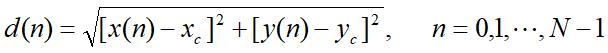
链码：
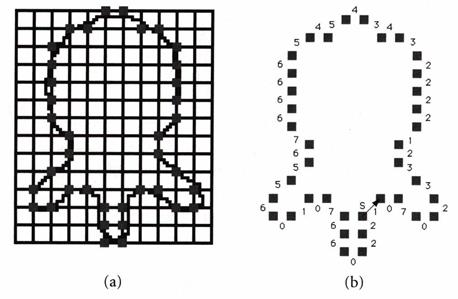
一个区域的形状也可以用对其边界上的连续点的相对位置量化的方式实现。

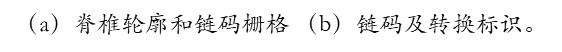
纹理测度

对医学图像的检验通常要对组织的外观做解释，例如平滑、粒度、规则性、均匀性等。这些属性都与图像的局部灰度变化有关，可以用纹理(Texture)测度量化：

• 统计矩：可以直接从图像的灰度直方图计算。
• 共生矩阵（Co-occurrence matrix）：从2D直方图计算，可以保留空间信息。
• 谱测度：由图像的Fourier变换得到，特别是当图像有重复的模式时。
• 分型维（Fractal dimension）：适合多尺度分析。
• 行程（Run-length）统计：适合分析图像中具有相同数值的像素组成的线性条块。

纹理可以是某一个选定的局部区域，也可以是整幅图像的特性。

统计矩

纹理是一种视觉感知的图像局部特征的综合。图像某一位置的纹理特征与这一位置周围的灰度变化规律密切相关。图像的平滑区域包含的像素灰度彼此接近，而粗糙区域的像素灰度有较大的变化，因此区域的直方图的统计矩可以作为描述图像纹理的测度。
如果一个图像区域有K个灰度等级，灰度均值是µ，该直方图的均值n阶矩定义为：

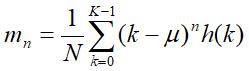
二阶矩m2又称方差，是较常用的纹理测度，描述图像的视觉粗糙程度，且相对易于计算。三阶矩和四阶矩分别称做倾斜度（Skewness）与峭度（Kurtosis），分别反映直方图的不对称性及均匀性。虽然这些测度确实与图像区域中灰度的变化有关，但并不总是能够反映图像的视觉纹理感受。但还是可以作为图像的特征提取出来进行定量计算，达到特定的模式识别目的。

灰度共生矩阵

灰度共生矩阵不仅包含灰度统计信息，而且反映灰度分布的空间信息。图像中相距（Δx,Δy）的两个灰度象素对同时出现的联合频数分布可用一个灰度共生矩阵表示。设图像共有K个灰度等级，则灰度共生矩阵的大小为KxK。灰度共生矩阵反映了图像灰度关于方向、相邻间隔及幅度变化的综合信息。从它出发，可以进一步提取描述图像纹理的一系列特征。
所谓空间信息是指灰度共生矩阵的元素值代表具有特定距离和方向的一对像素出现的频数。典型的方向有4个：0°，45°，90°，和135°。常用的距离d=1（对于θ=0°，90°），d= √2（对于θ=45°和135°）。一个大小为KxK的的灰度共生矩阵的矩阵元的数值是所有距离为d，与水平方向角度为θ的像素对数目之和。

例：
像素总数P=36的一个小片图像区域

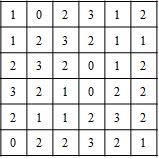
它的灰度共生矩阵H(√2,45°)

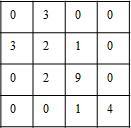
H(d,θ)的像素对总数P’ < P，P’=25
图像块的最上一行及最右列缺少成45°的像素对。当距离d增加时，这种情况就更突出。对更一般情况，设图像尺寸是M行N列。4个主要方向像素对总数P’的值分别是：

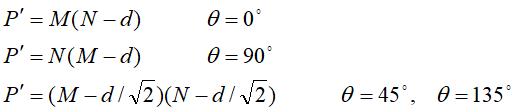
归一化灰度共生矩阵C(d,θ)的元素定义为：

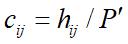
基于归一化灰度共生矩阵可以定义一系列纹理测度

1. 角二阶矩（能量） ：
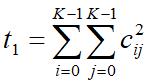   反映图像的均匀性。在均匀区灰度变化较小，大部分像素对具有相同或相近值。主要概率发生在 C(d,θ) 的对角线附近，其它大部分元素为零。
   非均匀区灰度变化大的像素对较多，在整个灰度共生矩阵上概率均匀分布，而且元素Cij的值都很小。所以，非均匀区的角二阶矩比均匀区的角二阶矩要小。该测度对区域内部有无灰度变化较敏感，但对灰度变化数值大小不敏感。即具有高的局部灰度对比度的区域角二阶矩值不一定高。
2. 惯量

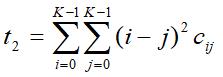
又称反差,由于是给 Cij加权，强调大灰度变化的作用，因此该测度对非均匀区的局部对比度敏感。非均匀区的惯量值大，均匀区的惯量值小。

3. 逆差矩
   
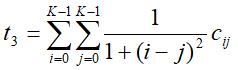
   对高对比度赋予低的权重
4. 熵

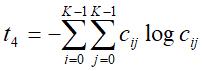
熵反映区域内的随机程度。当所有Cij都相等时熵有最大值。该测度可以用于区分有结构纹理的组织与缺少纹理的组织。

细化算法

骨架提取迭代技术

这是一种根据临近关系判断是否将一个边界点从二值化结构轮廓中消除从而实现轮廓细化的算法。要消除一个点必须满足一定的条件，即不能导致待细化区域的分裂。如果结构元素是1，背景像素是0的话，首先计算两个累加和的值。

第一步

第一步首先检测整幅图像，搜索边界像素。条件是该像素本身值是1，并且至少有一个8-连通像素值为0。在此基础上判断下述四个条件是否同时满足：
条件1：
$$2<=n(p_1)<=6$$
$$n(p_1)=p_2+p_3+p_4+p_5+p_6+p_7+p_8+p_9$$
大于等于2会保证p1点不是端点或孤立点，因为删除端点和孤立点是不合理的，小于等于6保证p1点是一个边界点，而不是一个内部点。等于0时候，周围没有等于1的像素，所以p1为孤立点，等于1的时候，周围只有1个灰度等于1的像素，所以是端点（注：端点是周围有且只能有1个值为1的像素)。

条件2：
$$s(p_1)=1$$
如果临域中有多于一个的0-1过渡，删除p1会导致区域分裂。
条件3：
$$p_2\ast p_4\ast p_6=0$$

条件4：
$$p_8\ast p_4\ast p_6=0$$
如果p4=0或p6=0或p2=p8=0，条件3和4同时满足，这三种情况分别对应下图的东边界(a)、南边界(b)、西北边界( c)。

如果以上四个条件都满足的话，将p1标记为“可删除”，遍历整幅图像后再对全部标记为“可删除”点统一删除。

第二步

第二步是将四个条件应用在第一步的结果上。前两个条件与第一步相同，后两个条件是：
条件3：
$$p_2+p_4+p_8=0$$
条件4：
$$p_8+p_2+p_6=0$$

这两个条件对应北边界、西边界和东南边界。在第二步也是先将满足四个条件的p1标记“可删除” 。在第二步完成之后， 对整幅图像中全部标记为“可删除”点统一删除。
算法开始新的一次迭代。即在第二步的结果之上做第一步处理，直到在两步中都没有像素被标记为“可删除”为止。算法产生一个由8-连通像素串构成的结构骨架。

优点：骨架提取迭代算法具有较高的效率。细化算法可以应用在冠状动脉血管树分析，肠胃内窥镜图像，DNA片段的原子力显微图像，眼底图像，以及染色体形状的量化。