二叉树的遍历：迭代实现

Posted 2021-07-17 You are my ghost

文章目录

• 二叉树的遍历：迭代实现
• • 迭代遍历的好处
  • 迭代遍历代码实现
  • • 前序遍历
    • 中序遍历
    • 后序遍历

二叉树的遍历：迭代实现

二叉树有两种遍历方式：递归实现以及迭代实现，递归实现相信大家已经非常熟悉，今天为大家介绍二叉树的迭代实现以及其代码实现；

迭代遍历的好处

我们都知道，递归调用的函数是存在中“栈”中的，但是栈的容量并不大；在进行递归实现时，如果构造的二叉树过大，容易栈溢出；

但是在使用迭代实现时，是将所遍历的节点存在已经开好的空间中，这个空间开在“堆”上，堆的容量可以认为是无限大的，便不存在溢出的问题。

迭代遍历代码实现

前序遍历

前序遍历：根节点->左孩子->右孩子；
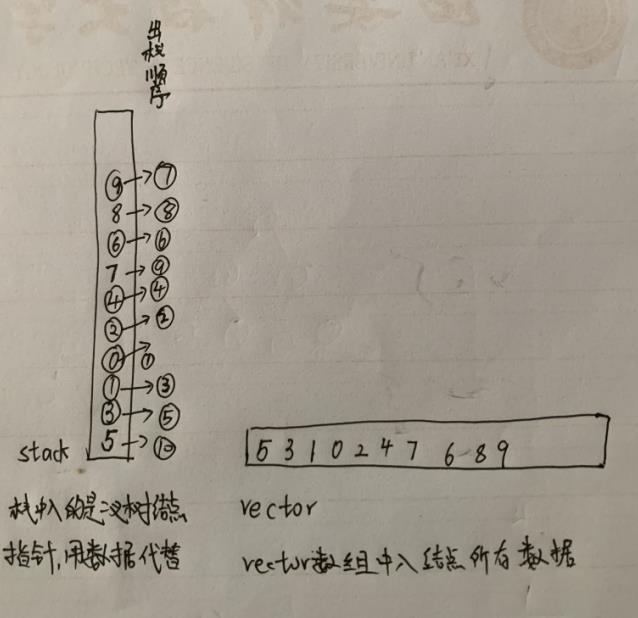
思路：定义一个当前节点cur=root，从cur开始一直向左孩子走，每遍历一个节点，若cur不为空，便将cur节点指针存入栈中，将cur节点数据存入vector数组中，直到左孩子为空；这时cur为栈顶，也为该支链最后一个左孩子，然后去访问cur的右孩子（cur=top->right），再将栈顶pop（出栈），依然边入栈边入vector数组；遍历完该支链后会回到上一层，遍历上层节点的左支链；以此类推。

以上述二叉树为例，前序遍历的结果为{5，3，1，0，2，4，7，6，8，9}，

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution 
{
public:
    vector<int> preorderTraversal(TreeNode* root) 
    {
        vector<int>v;
        stack<TreeNode*>st;
        TreeNode*cur=root;
        while(cur||!st.empty())
        {
            while(cur)
            {
                st.push(cur);
                v.push_back(cur->val);
                cur=cur->left;
            }
            TreeNode* top=st.top();
            cur=top->right;
            st.pop();
        }
        return v;
    }
};

中序遍历

中序遍历的思路与前序遍历相同，唯一不同的操作时是在访问到最后一个左孩子之后再在vector数组中插入数据；

中序遍历：左孩子->根节点->右孩子；
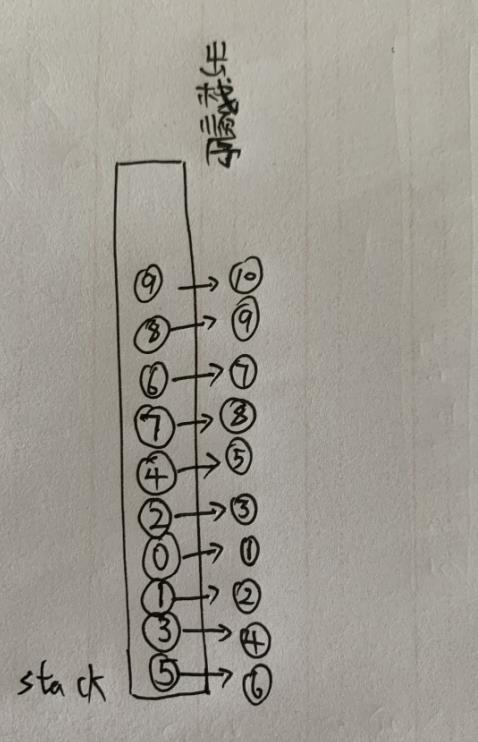
思路：定义一个当前节点cur=root，从cur开始一直向左孩子走，每遍历一个节点，若cur不为空，便将cur节点指针存入栈中，直到左孩子为空；这时cur为栈顶，也为该支链最后一个左孩子，将cur节点数据存入vector数组中，然后去访问cur的右孩子（cur=top->right），再将栈顶pop（出栈），依然访问到最后一个左孩子后边在vector数组入数据边出栈；遍历完该支链后会回到上一层，遍历上层节点的右支链；以此类推。

以上述二叉树为例，中序遍历的结果为{0，1，2，3，4，5，6，7，8，9}，

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) 
    {
        vector<int>v;
        stack<TreeNode*>st;
        TreeNode*cur=root;
        while(cur||!st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }
            TreeNode*top=st.top();
            v.push_back(top->val);
            cur=top->right;
            st.pop();
        }
        return v;
    }
};

后序遍历

后序遍历的难度略有提升，在后续遍历时，需要避免父亲节点的二次访问；

思路：定义一个当前节点cur=root，已访问节点的父亲节点prev=nullptr，从cur开始一直向左孩子走，每遍历一个节点，若cur不为空，便将cur节点指针存入栈中，直到左孩子为空；这时定义top=cur为栈顶，也为该支链最后一个左孩子，如果top->right不为空且不为prev，则将top节点数据存入vector数组中，然后出栈，这时top为上一个已访问节点的父亲节点，所以令prev=top便可以去继续访问上一层的右子树，如果top->right不为空或未访问，便访问top的右树；以此类推。

以上述二叉树为例，中序遍历的结果为{0，2，1，4，3，6，9，8，7，5}，

class Solution 
{
public:
    vector<int> postorderTraversal(TreeNode* root) 
    {
        vector<int>v;
        stack<TreeNode*>st;
        TreeNode*cur=root;
        //prev存已访问节点的父亲节点
        TreeNode*prev=nullptr;
        while(cur||!st.empty())
        {
            //保存左路节点路线
            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }
            TreeNode*top=st.top();
            //如果此时top的左孩子为空或者已经访问，说明右树已经访问完了或无右树，
            //便将数据存入vector数组并出栈；访问根节点并返回上一层，继续访问上一层的右树。
            if(top->right==nullptr||top->right==prev)
            {
                v.push_back(top->val);
                st.pop();
                prev=top;
                cur=nullptr;
            }
            //top->right不为空或未访问，便访问top的右树
            else
            {
                cur=top->right;
            }
        }
        return v;
    }
};