密码学基础
Posted 平原上的维克多
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了密码学基础相关的知识,希望对你有一定的参考价值。
本文主要内容来自山东大学孔凡玉教授开设的《大数据安全》课程,更新中…
密码学是信息安全的核心理论。
密码学的特性及功能:
特性:
- 机密性(Confidentiality):非授权者无法获取明文内容。
- 完整性(Integrity):接收者能够验证消息是否在传输过程中被增加、删除、修改。
- 真实性(Authenticity):接收者能够确认消息来源的真实性。
- 不可抵赖性(Nonrepudiation):发送者无法否认其签发的消息。
功能:
- 数据加密:机密性(对称密钥)
- 消息鉴别:完整性和真实性(杂凑函数 HMAC)
- 身份鉴别:真实性(公钥密码)
- 数字签名:不可抵赖性(公钥密码)
对称密码
DES算法流程
明文和密文长度都是64位,密钥长度为56位。
令
I
P
(
M
)
=
L
0
R
0
IP(M)=L_{0}R_{0}
IP(M)=L0R0,其中
∣
L
0
∣
=
∣
R
0
∣
=
32
|L_{0}|=|R_{0}|=32
∣L0∣=∣R0∣=32。
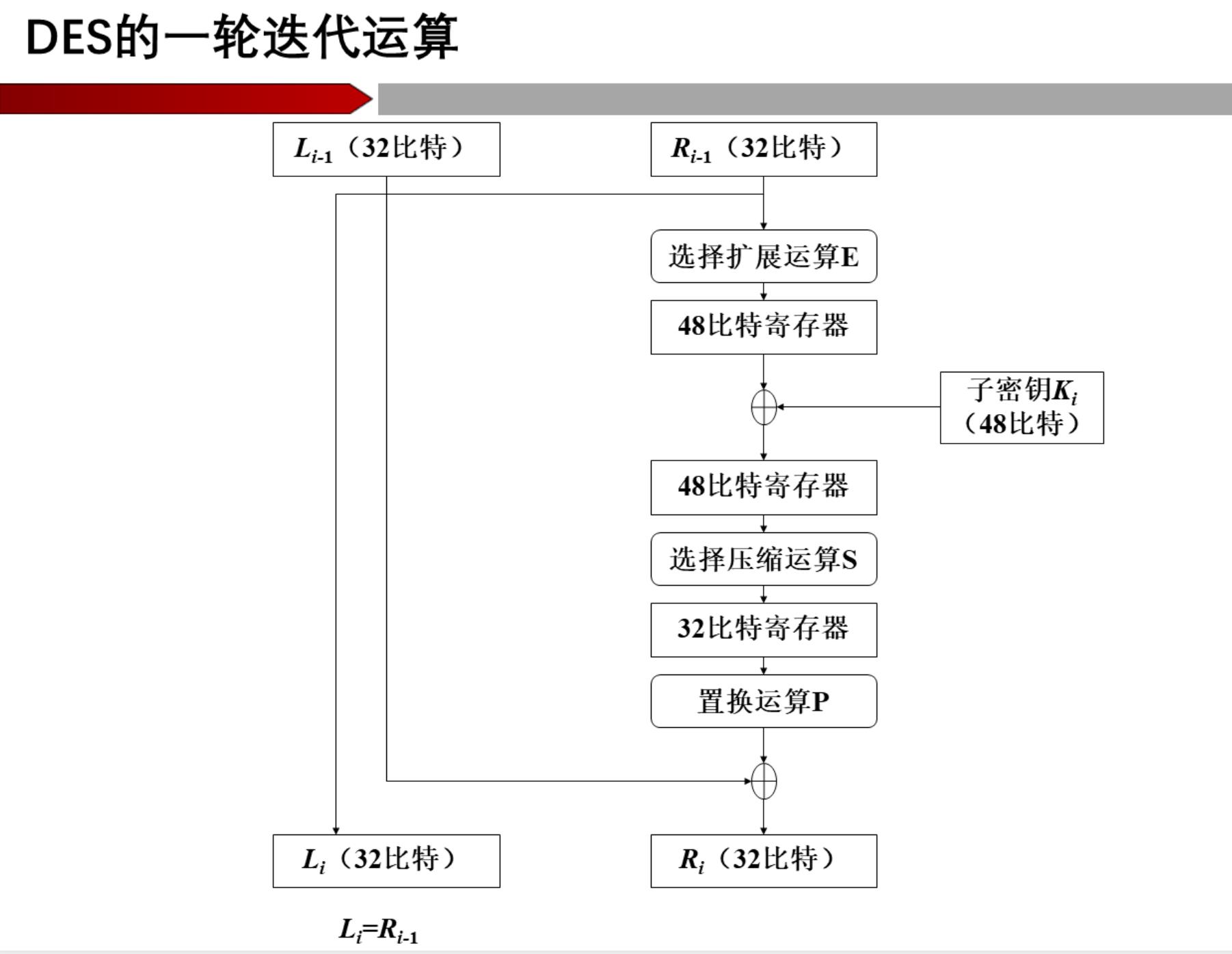
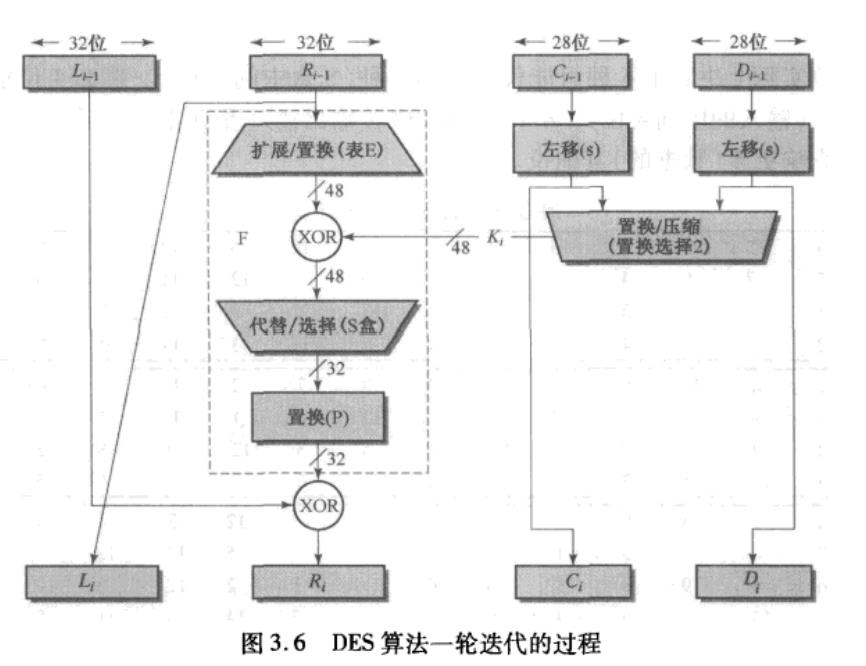
对i=1,2,…16,依次执行下列操作:
- 记第i轮中密钥为 K i K_{i} Ki( K i K_{i} Ki由 K i − 1 K_{i-1} Ki−1通过循环左移再压缩成48位),
- 32位的 R i − 1 R_{i-1} Ri−1利用表E扩展/置换为48位之后,
- 与48位的密钥 K i K_{i} Ki进行异或,
- 再利用S盒压缩/置换为32位,
- 然后利用置换函数P进行置换,
- 最后与 R i − 1 R_{i-1} Ri−1进行异或得到 R i R_{i} Ri;
- R i − 1 R_{i-1} Ri−1直接赋值给 L i L_{i} Li。
最终
C
=
I
P
−
1
(
L
16
,
R
16
)
C=IP^{-1}(L_{16},R_{16})
C=IP−1(L16,R16)
影响DES安全强度的因素:
- 轮运算数
- 置换函数的复杂度(比如是否非线性等)
- 密钥的长度
56位的密钥已经具备暴力破解可行性,因此我们使用某些方式增强其保密强度:
3-DES
既然56位的密钥存在被破解的可能性,那么我们就通过增加密钥的数量和加密的次数从而相应增大密钥的长度,
C = E ( D ( E ( P , K 1 ) , K 2 ) , K 3 ) C=E(D(E(P, K_{1}), K_{2}), K_{3}) C=E(D(E(P,K1),K2),K3)
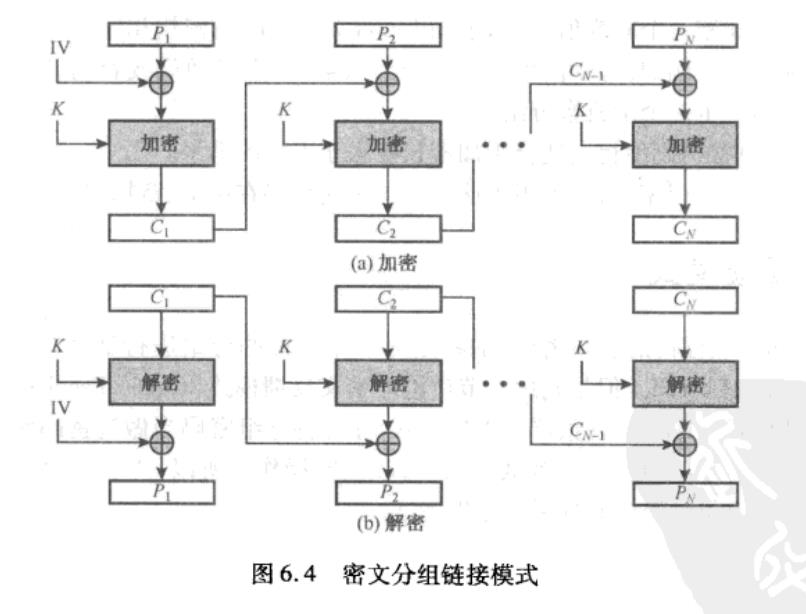
电码本(ECB)模式
简单高效可并行,分组之间便于进行差错控制;
相同的明文加密后得到相同的密文,抗已知明文攻击能力差。
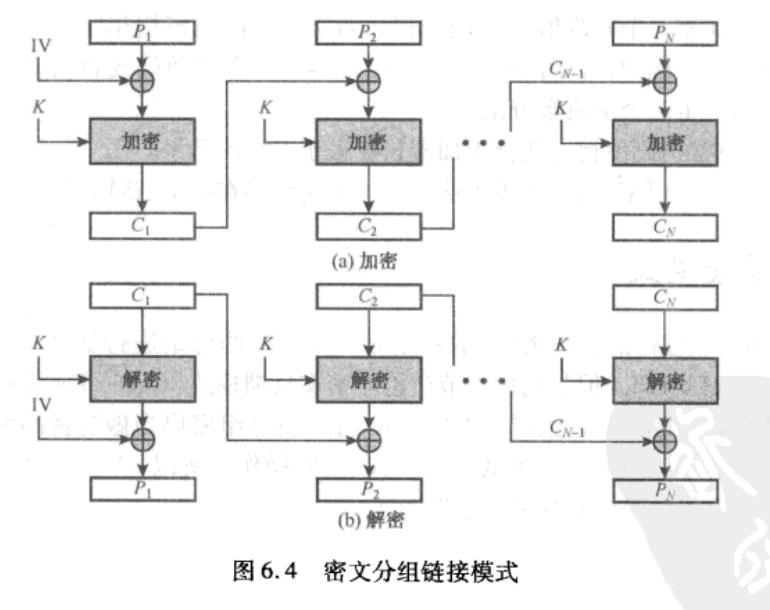
密文分组链接(CBC)模式
安全性高;
加密不可并行,解密可以并行。
HASH密码杂凑算法
杂凑函数H能将任意长度的消息M映射为较短的固定长度的值H(M)。
有效性:
H
(
x
)
H(x)
H(x)能够快速计算杂凑值。
抗原像性:给定
h
h
h,找到
x
x
x使得
h
=
H
(
x
)
h=H(x)
h=H(x)在计算上不可行。
抗弱碰撞性:给定
x
x
x,找到
y
y
y,使得
H
(
x
)
=
H
(
y
)
H(x)=H(y)
H(x)=H(y)在计算上不可行。
抗强碰撞性:找到
x
x
x和
y
y
y,使得
H
(
x
)
=
H
(
y
)
H(x)=H(y)
H(x)=H(y)在计算上不可行。
通用模型:
- 将原始消息 M M M划分为固定长度的块 Y i Y_{i} Yi,最后一块进行padding使其包含M的长度。
- 设定压缩函数 f f f和初始值 C V 0 CV_{0} CV0,
- 令 C V i = f ( C V i − 1 , Y i − 1 ) CV_{i}=f(CV_{i-1}, Y_{i-1}) CVi=f(CVi−1,Yi−1),最后一个 C V i CV_{i} CVi即为hash值。
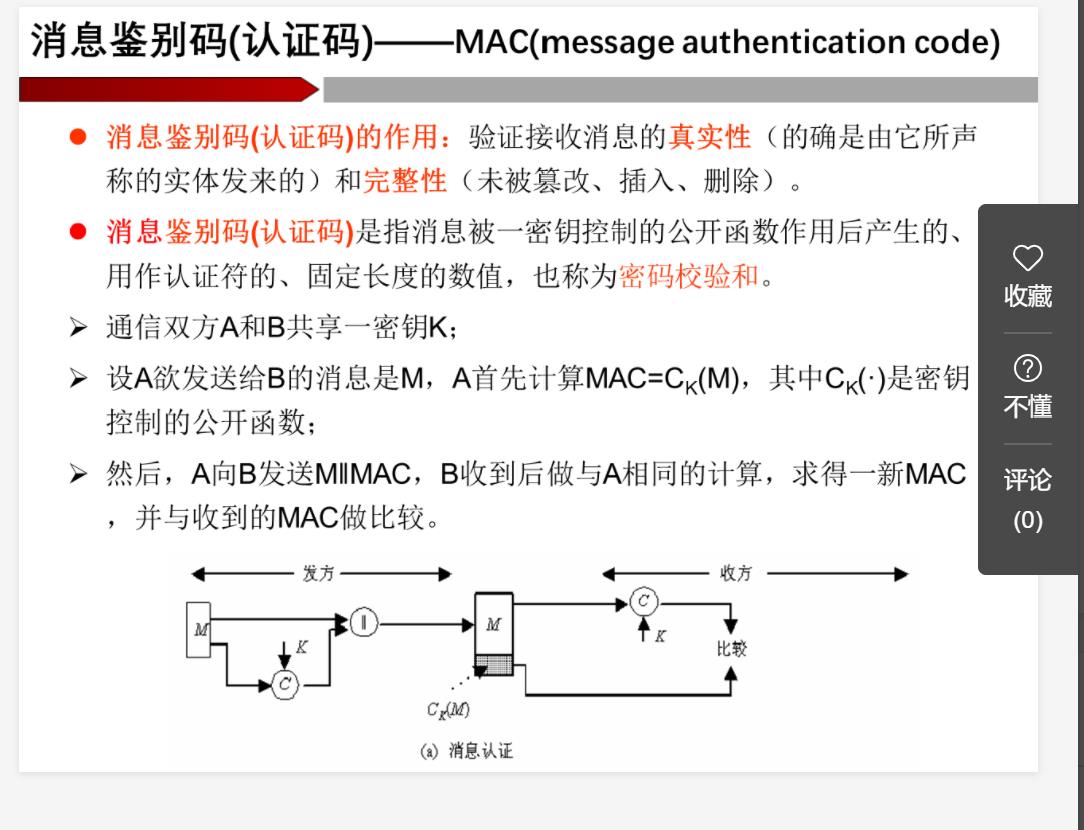
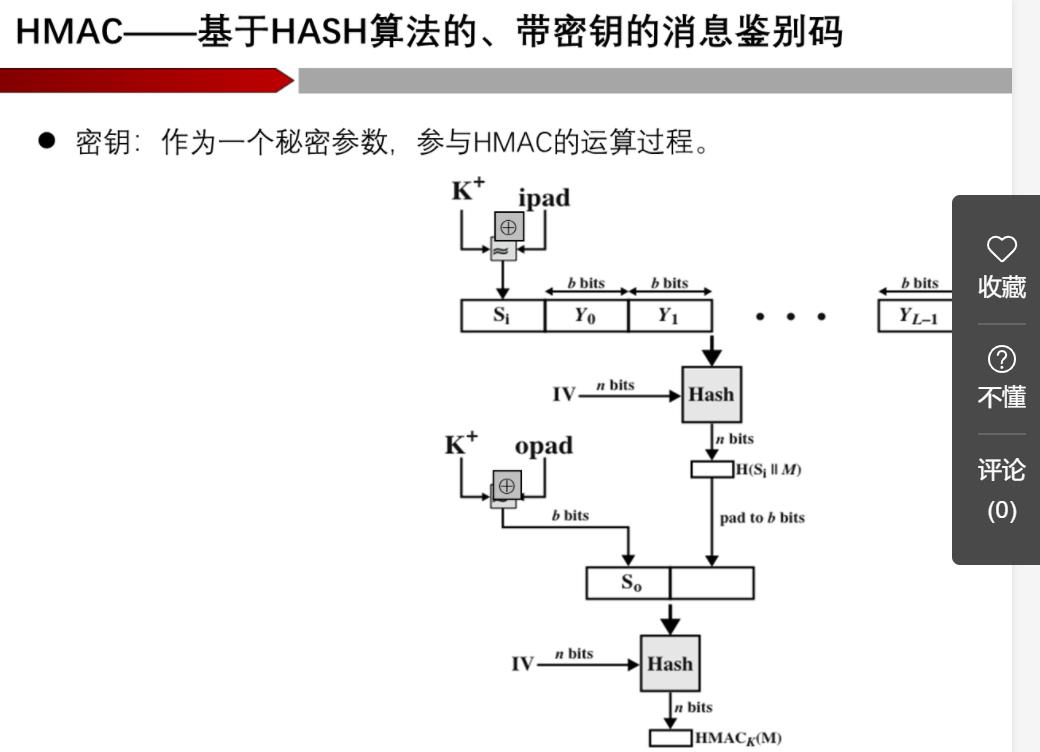
消息鉴别码
从代替和置换走向数学函数 ——公钥密码
关于公钥密码与对称密码之间的区别的两个误区:
1、安全性
2、先进性
但是公钥密码确实拥有独特的优点:
1、密钥管理
2、满足数字签名的需求
RSA算法
- 选定素数 p p p和 q q q,令 n = p q n=pq n=pq
- 求出满足 g c d ( ϕ ( n ) , e ) = 1 gcd(\\phi (n), e)=1 gcd(ϕ(n),e)=1的 e e e,且 1 < e < ϕ ( n ) 1<e<\\phi(n) 1<e<ϕ(n)
- 求出满足 d e m o d ϕ ( n ) = 1 de\\ mod\\ \\phi(n) = 1 de mod ϕ(n)=1的 d d d
故公钥为
P
U
=
e
,
n
PU={e, n}
PU=e,n,私钥为
P
R
=
d
,
n
PR={d, n}
PR=d,n。
对明文分组
M
M
M和密文分组
C
C
C,加密和解密的过程如下:
C
=
M
e
m
o
d
n
C = M^{e}\\ mod\\ n
C=Me mod n
M
=
C
d
m
o
d
n
=
M
d
e
m
o
d
n
M = C^{d}\\ mod\\ n = M^{de}\\ mod\\ n
M=Cd mod n=Mde mod n
安全性分析:
密码攻击者攻击RSA体制的关键点在于如何分解
N
N
N,若分解成功使得
N
=
p
q
N=pq
N=pq,
则可以算出
ϕ
(
N
)
=
(
p
−
1
)
(
q
−
1
)
\\phi (N) = (p-1)(q-1)
ϕ(N)=(p−1)(q−1),然后由公开的
e
e
e解出秘密的
d
d
d。
若使RSA安全,
p
p
p和
q
q
q必须是足够大的素数,使得攻击者无法在有效时间内将其分解。
Diffie-Hellman密钥交换
本原根的定义:…
对任意整数b和素数p的本原根a,我们可以找到唯一的指数使得
b = a^i(mod p) (0<=i<=p-1)
指数i称作b的以a为底的模p离散对数 dlog_{a,p}(b)
该协议仅当通信双方的真实性能够得到保证时是安全的 => 计算大素数的离散对数极其困难 => 使两个用户能够安全地交换密钥以便在后续的通信中用该密钥对消息进行加密
公开p和a,通信双方分别选定
X
A
X_{A}
XA和
X
B
X_{B}
XB,计算并公开:
Y
A
=
a
X
A
m
o
d
p
Y_{A} = a^{X_{A}} mod p
YA=aX密码学基础