GNN笔记：图卷积

Posted 2021-07-16 刘文巾

1 graph和卷积

在机器学习笔记：CNN卷积神经网络_刘文巾的博客-CSDN博客中，我们知道，因为图像具有“管中窥豹”、“相同模式”、“降采样”三个特点。所以我们可以用一个很小的卷积核对图像进行卷积操作。换言之，就是图像具有局部平移不变性。

那么graph有没有这种性质呢？没有

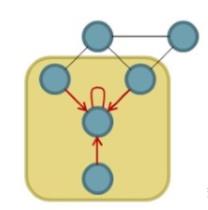
graph结构不规则，所以其不存在平移不变性。每个节点周围的邻居数不固定。所以传统的CNN无法应用于网络中。换言之，在空域上的图，是没法进行卷积操作的。

2. Graph Convolution

那么，既然无法直接在空域进行卷积，可否将graph映射到频域后再做卷积操作呢？

在GNN笔记：卷积_刘文巾的博客-CSDN博客 中，我们知道 卷积定理

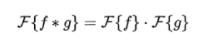
我们将等号两边加以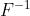，有：

我们记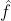为f的傅里叶变换结果，在GNN 笔记：图上的傅里叶变换_刘文巾的博客-CSDN博客 中，我们知道

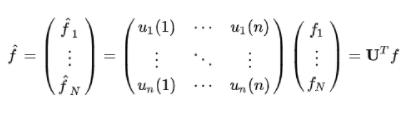
其中U是graph的拉普拉斯矩阵的特征向量组成的矩阵

而在线性代数中，我们还有一个结论。就是对于两个列向量u和v，它们的内积等同于将一个的元素放到对角矩阵的对角元上（矩阵其他位置的元素为0），然后这个对角矩阵和另一个列向量坐矩阵乘法。

证明：假设原来两个向量是 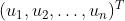和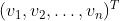

它们的内积结果是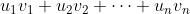

我们将u的元素放到对角矩阵的对角元上，那么我们有：

这个矩阵和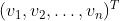内积，结果就是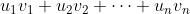

回到我们的图卷积中，利用上面的结论，我们有

                 

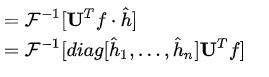
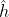
而同样在GNN 笔记：图上的傅里叶变换_刘文巾的博客-CSDN博客 中，我们说了图傅里叶变换的逆变换：

那么逆变换的式子带入图卷积的公式中，我们有

                 

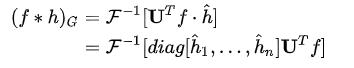
那么还有一个问题，为什么上面的图卷积公式中f就是f，h要写成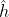,而不是像f一样的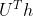呢？

       这是因为在 GCN 中我们的卷积核（即h相关的内容）是可训练并且参数共享的，所以在此我们可以直接将  写成，这个便是深度学习中的可学习参数。