算法优化：优化缓存访问模式

Posted 2021-04-02 算法杂话

• 1. 低效的循环嵌套

• 2. 随机访问模式

• 3. 数据复用

• 3.1 分块-空间局部性

• 3.2 分块-时间局部性

• 3.3 循环合并

1. 低效的循环嵌套

举例说明：

Figure 1. Inefficient Loop Nesting

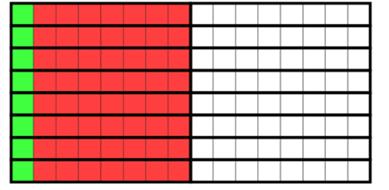
由于数组是按行优先顺序存储，而程序是按列对数组元素进行访问。如果数组大小 > L1 cache， 则最外层循环(outer loop)每次迭代都需要将数组重新加载到cache中，导致频繁的缓存未命中，从而导致程序性能变差。

修改方法：

Figure 2. Efficient Loop Nesting

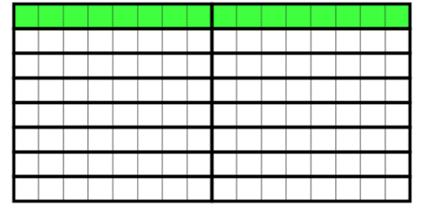
2. 随机访问模式

随机访问模式：在一个具有良好时间局部性的程序中，被引用过一次的内存位置很可能在不久的将来再被引用多次；在一个具有良好空间局部性的程序中，如果一个内存位置被引用了一次，程序很可能会在不久的将来引用附近的一个内存位置。不符合局部性的内存访问模式即随机访问模式(Random Access Pattern)。

随机访问模式产生的原因：

• 数据结构，例如链表、树结构以及哈希表
• 动态内存分配-内存碎片
• 算法相关，例如深度优先搜索算法

优化缓存访问模式的常见方法：

3. 数据复用

3.1 分块-空间局部性

(1) 矩阵转置

假设矩阵是按行优先顺序存储。矩阵src按行访问元素，矩阵dst按列访问元素(与存储顺序不同)。如果矩阵dst比较大，不能装入到cache中，将出现前面提到的“低效的循环嵌套”的问题。修改的方法是对src进行分块处理，每次只处理src的BLOCK列，则

通过分块处理，第一次jb循环只处理src的第 列，第二次jb循环只处理src的第 列，以此类推。如果选择的BLOCk足够小，那么每次jb循环中dst的对应行能够缓存到cache中，从而减少cache miss，提高程序性能。

(2) 矩阵乘法

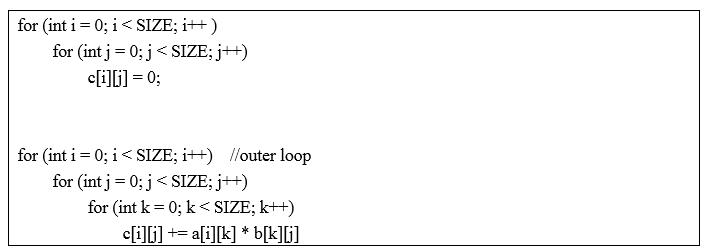
数组b按列访问元素，因此对数组b进行分块。

也可以同时对数组a, b和c进行分块：

3.2 分块-时间局部性

在迭代算法中，每个元素的第(k)次的结果是在第(k-1)次的结果上计算得到。如果迭代算法处理的输入数据的规模比较大，可以对数据进行分块，对每个数据对象执行尽可能多的操作，从而提高程序的时间局部性。

举例说明：

对于每个数据a[j]，执行了iter次迭代，如果数组a很大，则outer loop每迭代一次，都需要把数组a重新装入cache中，导致cache miss增加，程序性能变差。修改的方法是对数组a进行分块，分别对不同的数据块进行尽可能多的迭代处理。

3.3 循环合并

由于第一个for循环和第二个for循环都使用到vector数组，因此可以合并两个for循环。