二叉搜索树的图文详解

Posted 2021-07-16 AllenSquirrel

二叉搜索树的实现

• 二叉搜索树的结构

二叉搜素树具备以下性质：

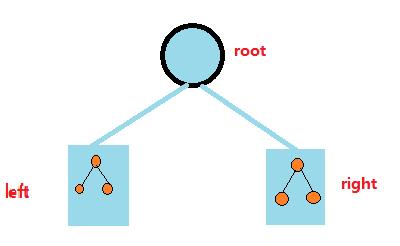
• 左子树不为空，则左子树上所有节点值都小于根结点值
• 右子树不为空，则右子树上所有节点值都大于根结点值
• 左右子树依然具备二叉树的以上性质

例如：

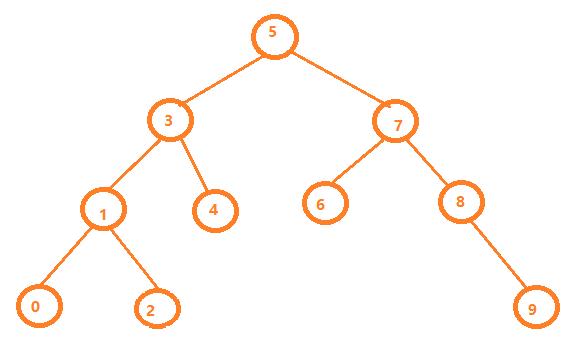
上图所建立的为二叉搜索树，根据其性质，按照中序遍历，可以获取一个递增有序序列【0,1,2,3,4,5,6,7,8,9】

根据以上性质，定义结构，包括每一个节点及左右节点定义和树的创建  具体代码如下：

template<class T>
struct BSTNode
{
	BSTNode(const T& data = T())
		: _pLeft(nullptr), _pRight(nullptr), _data(data)
	{}
	typedef BSTNode<T> Node;
	Node* _pLeft;
	Node* _pRight;
	T _data;
};
template<class T>
class BSTree
{
public:
	typedef BSTNode<T> Node;
	BSTree()
		:_root(nullptr)
	{}

	//深拷贝
	Node* copy(Node* root)
	{
		if (root == nullptr)
			return nullptr;
		Node* newnode = new Node(root->_data);
		newnode->_pLeft=copy(root->_pLeft);
		newnode->_pRight = copy(root->_pRight);
	}
	
	BSTree(const Node& btree)
		:_root(copy(btree._root))
	{

	}
    ~BSTree()
	{
		if (_root)
		{
			destory(_root);
			_root = nullptr;
		}
	}

private:
	Node* _root;
};

上述代码中，完成对搜索二叉树的结构定义，与普通二叉树基本一致，也就是说，二叉搜索树在二叉树的结构上变形得到，结构相同，只是在值的大小关系进行调整，使得满足二叉搜索树的性质。

• 二叉搜索树查找

查找逻辑：

若根结点不为空：

       若根结点key==目标查找key，则找到返回true

       若根结点key<目标查找key，则在右子树继续查找

      若根结点key>目标查找key，则在左子树继续查找

否则，返回false

图解如下：

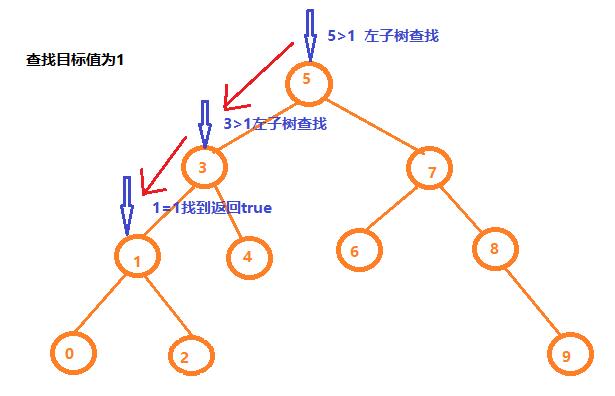
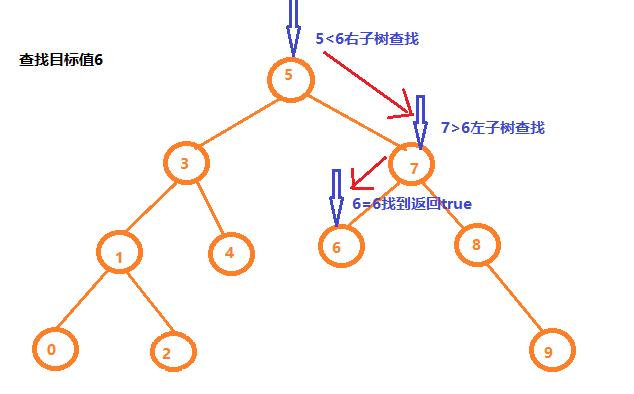
代码如下：

Node* find(const T& val)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_data == val)
				return cur;
			else if (cur->_data < val)
			{
				cur = cur->_pRight;
			}
			else
				cur = cur->_pLeft;
		}
	}

测试结果如下，同一层为同一种颜色标记，为方便展示，仅展示左子树部分

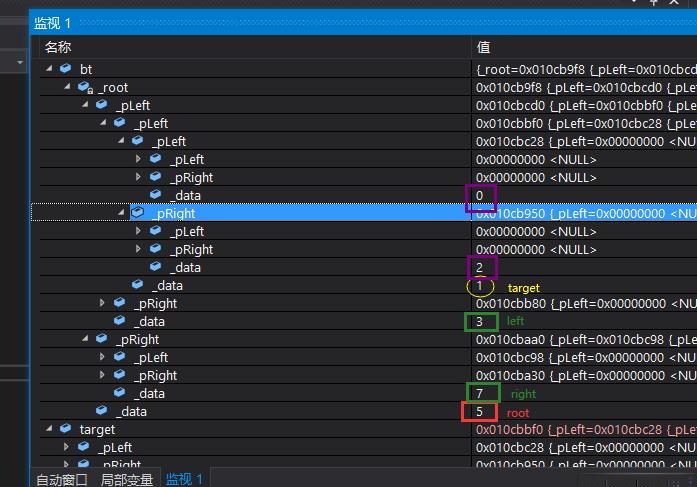
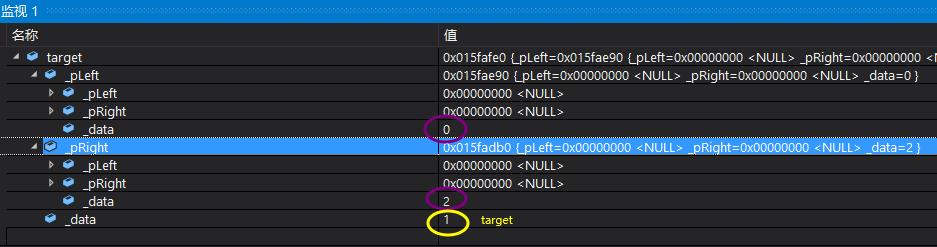
• 二叉搜索树插入

插入逻辑：

如果树为空（左右子树不存在），直接插入，返回true；

如果树不为空，按照二叉搜索树性质进行搜索，找到合适的插入位置，插入新节点

注意：重复节点无法插入，如果插入节点已经存在则报错返回

图解如下：

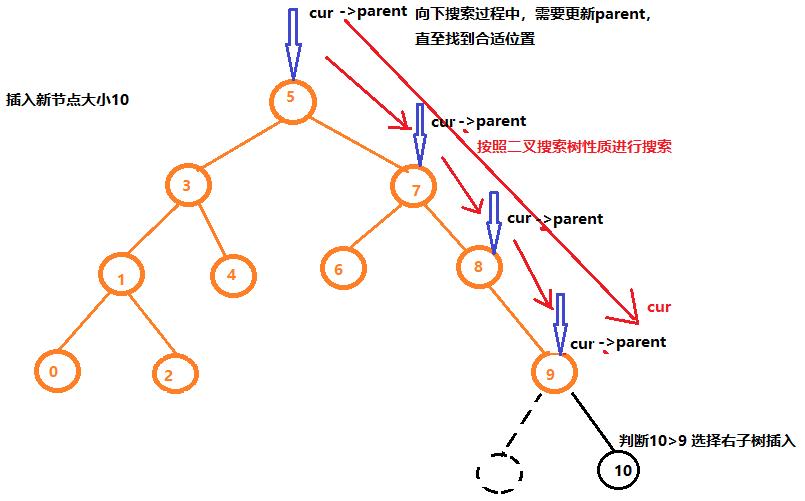
代码如下：

bool insert(const T& val)
	{
		if (_root == nullptr)
		{
			_root = new Node(val);
			return true;
		}
		//搜索
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			parent = cur;//更新父节点
			if (cur->_data == val)
				return false;
			else if (cur->_data < val)
			{
				cur = cur->_pRight;
			}
			else
				cur = cur->_pLeft;
		}
		//插入
		cur = new Node(val);
		if (parent->_data > val)
		{
			parent->_pLeft = cur;
		}
		else
			parent->_pRight = cur;
	}

测试结果如下：

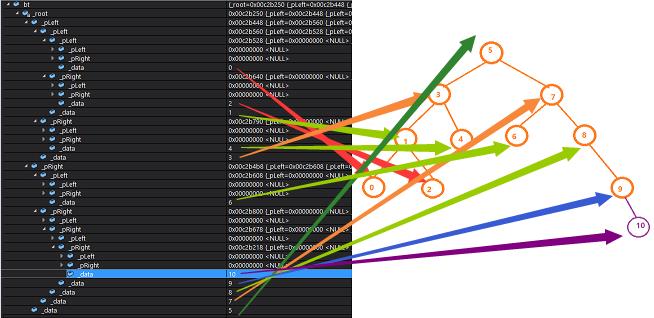
• 二叉搜索树的删除

删除逻辑：

通过搜索，查找要删除的节点是否在二叉搜索树中存在，如果不存在，则返回false

如果存在，则考虑下述四种情况：

1. 要删除的节点无孩子节点
2. 要删除的节点只有左孩子节点
3. 要删除的节点只有右孩子节点
4. 要删除的节点左右孩子节点都存在

对于情况1：如果删除节点为根结点，则将根结点为nullptr，如果删除节点为该节点的左孩子，则将该节点的左孩子节点为nullptr，如果删除节点为该节点的右孩子，则将该节点的右孩子节点为nullptr

对于情况2：要删除的节点只存在左孩子节点，无右孩子节点，

                    如果删除节点为根结点，则将左孩子节点连接在根结点

                    如果删除节点非根结点，则判断删除节点位于父节点的位置，如果在父节点左边，则将左孩子节点连接在父节点左边，否则连接在父节点右边

对于情况3：要删除的节点只存在右孩子节点，无左孩子节点，

                    如果删除节点为根结点，则将右孩子节点连接在根结点

                    如果删除节点非根结点，则判断删除节点位于父节点的位置，如果在父节点左边，则将右孩子节点连接在父节点左边，否则连接在父节点左边

对于情况4：左右子节点都存在

                    创建新节点:

                                           1  左子树最大节点: 左子树的最右节点  

                                           2  右子树最小节点: 右子树的最左节点
                    此处假设左子树的最右节点为新结点，将其初始化当前删除节点的左节点，并一直在其左子树中找到最右节点为止

                    找到左子树最右节点与当前删除节点的值进行交换

                   判断左子树最右节点位于父节点的位置，如果在父节点左边，则将其左孩子节点连接在父节点左边，否则连接在父节点右边

图解如下：

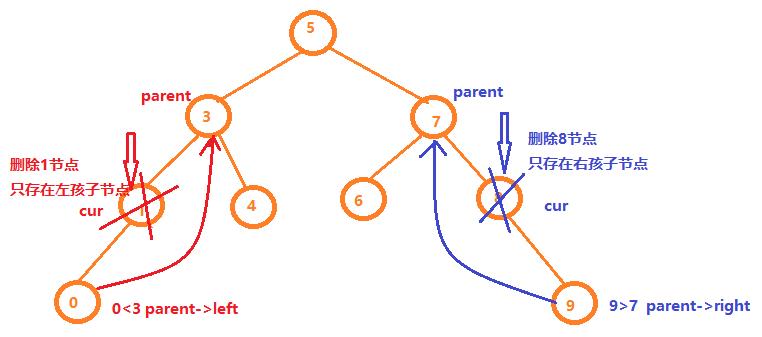
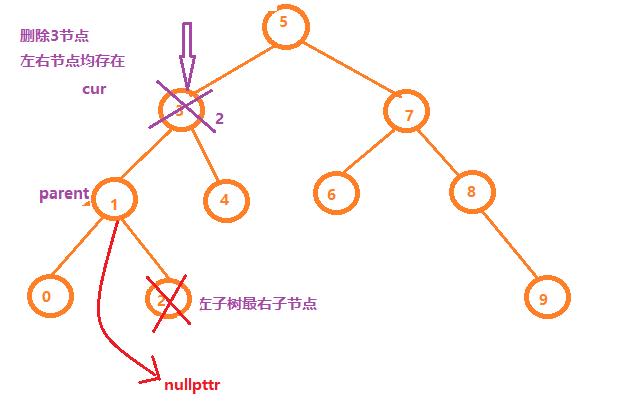
代码如下：

bool erase(const T& val)
	{
		//搜索
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			parent = cur;//更新父节点
			if (cur->_data == val)
				break;
			else if (cur->_data < val)
			{
				cur = cur->_pRight;
			}
			else
				cur = cur->_pLeft;
		}
		if (cur == nullptr)
			return false;
		//删除
		//(1)删除节点为叶子节点
		if (cur->_pLeft == nullptr&&cur->_pRight == nullptr)
		{
			if (cur == _root)//判断是否为根结点
				_root = nullptr;
			else
			{
				if (parent->_pLeft == cur)
					parent->_pLeft = nullptr;
				else
					parent->_pRight = nullptr;
			}
			delete cur;
		}
		//(2)非叶子节点
		else if (cur->_pLeft == nullptr)//只存在右子树
		{
			if (cur == _root)//判断是否为根结点
				_root = cur->_pRight;
			else
			{
				if (parent->_pLeft == cur)//判断删除节点在父节点左右位置
					parent->_pLeft = cur->_pRight;
				else
					parent->_pRight = cur->_pRight;
			}
			delete cur;
		}

		else if (cur->_pRight == nullptr)//只存在左子树
		{
			if (cur == _root)//判断是否为根结点
				_root = cur->_pLeft;
			else
			{
				if (parent->_pLeft == cur)//判断删除节点在父节点左右位置
					parent->_pLeft = cur->_pLeft;
				else
					parent->_pRight = cur->_pLeft;
			}
			delete cur;
		}
		else
		{
			//左右子树都存在
			//新的根节点:左子树最大节点  左子树的最右节点   右子树最小节点  右子树的最左节点
			//假设左子树的最右节点
			Node* leftrightMost = cur->_pLeft;
			parent = cur;
			while (leftrightMost->_pRight)//如果左子树的右不为空  一直找最右节点
			{
				parent = leftrightMost;
				leftrightMost = leftrightMost->_pRight;
			}
			//交换
			swap(cur->_data,leftrightMost->_data);
			//删除
			if (parent->_pLeft == leftrightMost)
				parent->_pLeft = leftrightMost->_pLeft;
			else
				parent->_pRight = leftrightMost->_pLeft;
			delete leftrightMost;
		}

	}

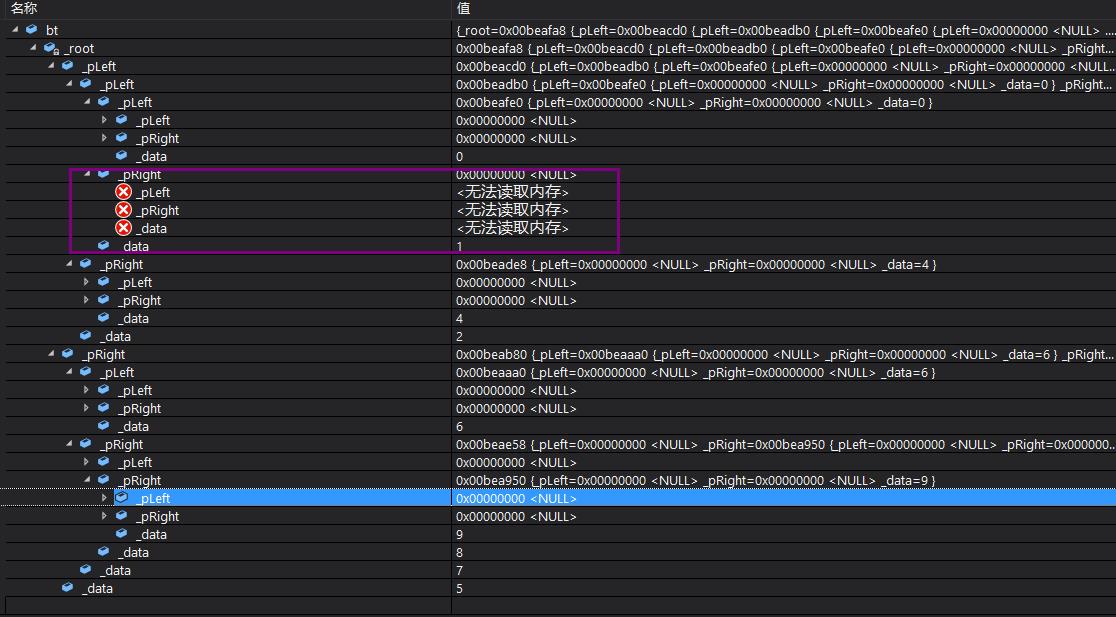
测试结果如下：

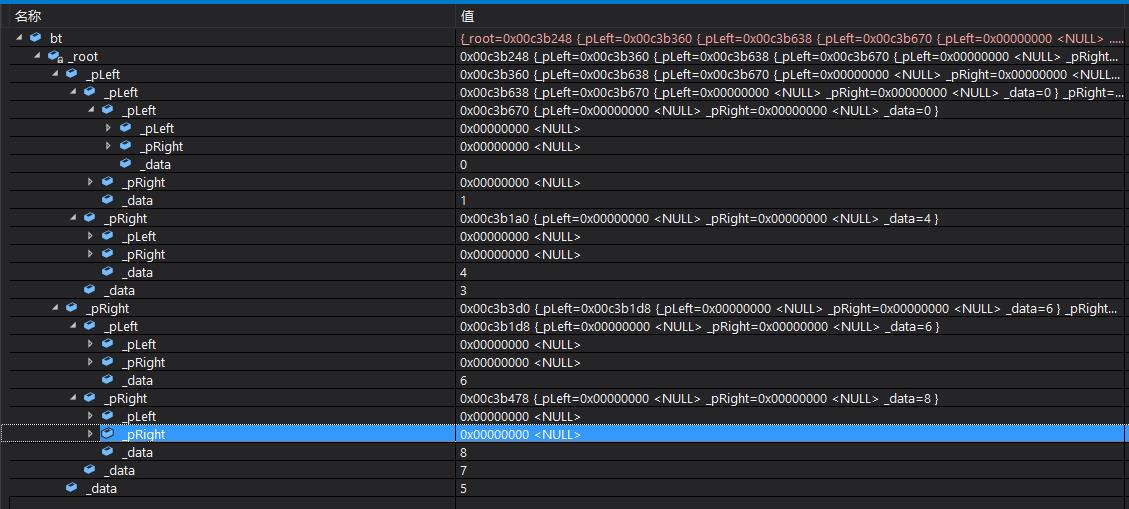
删除节点1  和  8  

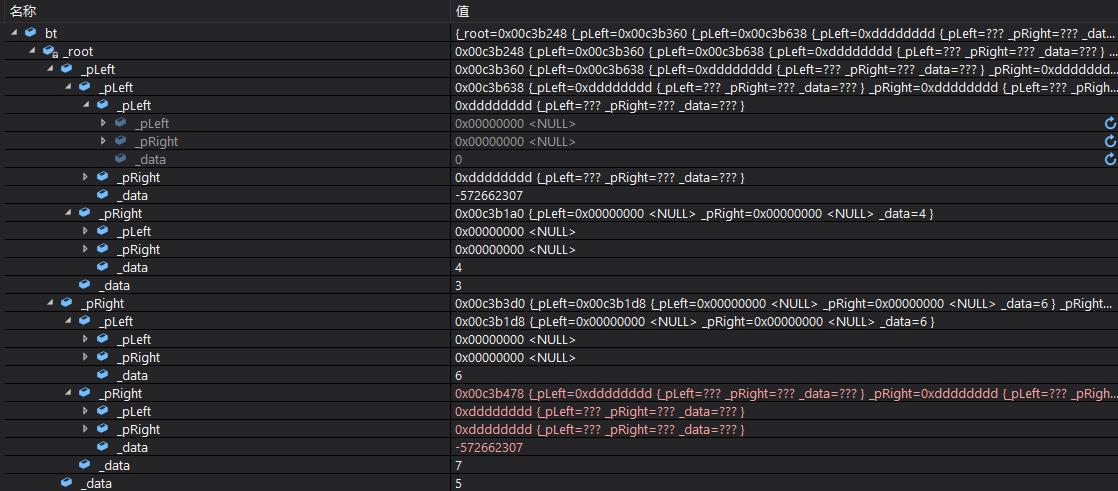
删除节点3