AVL树的实现（图文详解）

Posted 2021-07-16 AllenSquirrel

AVL树的实现

• AVL树定义

AVL树其实就是一棵特殊的二叉树，为什么会出现AVL树，AVL树比普通二叉树优势在什么地方呢？

我们知道，一棵普通的二叉搜索树，以其特殊的性质（左<根<右），中序遍历将得到有序的序列，同时在搜索目标值时可以根据其性质加快搜索，但数据如果有序或接近有序，二叉搜索树会退化成为单支树，查找目标值相当于在顺序表中查找，时间复杂度从O(lgn)退化到O(n)

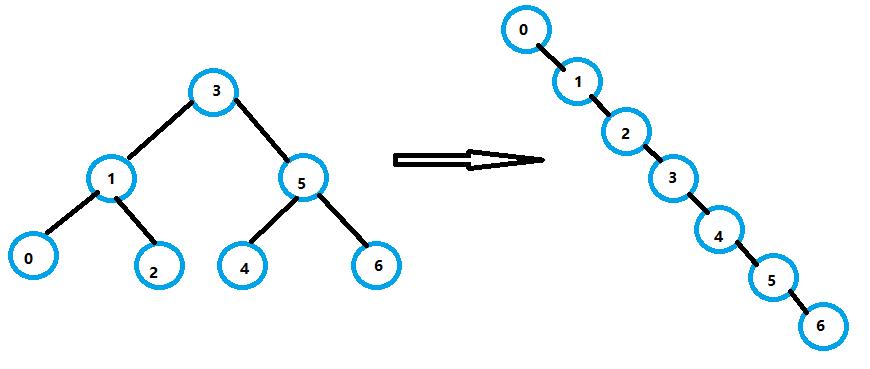
具体参见二叉搜索树图文详解

AVL树为了解决上述问题，规定其性质：

1. 左右子树均是AVL树
2. 左右子树的高度之差(平衡因子)不超过1（1/-1/0）

当在AVL树中插入一个新节点，通过对节点进行调整，保证高度之差不超过1，从而降低树高度，缩短搜索路径

• 平衡因子

性质：

• 判断对应二叉树是否平衡的一个整型值
• 每一个节点都存在一个平衡因子，来表示二叉树是否平衡
• 平衡因子=右子树的层数-左子树的层数
• 平衡因子范围（-1~1）

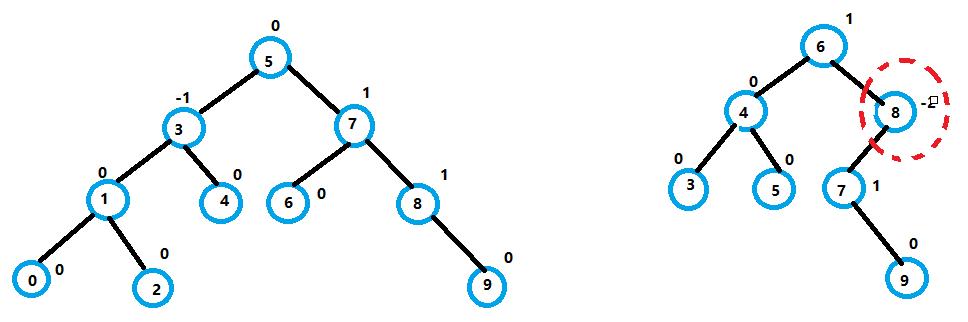
• 结构定义

AVL树结构与二叉搜索树结构类似，除左右孩子节点，数据外，添加父节点，平衡因子bf

template<class T>
struct AVLTreeNode
{
	AVLTreeNode(const T& data)
		: _left(nullptr), _right(nullptr), _parent(nullptr)
		, _val(data), _bf(0)
	{}
	AVLTreeNode<T>* _left; // 该节点的左孩子
	AVLTreeNode<T>* _right; // 该节点的右孩子
	AVLTreeNode<T>* _parent; // 该节点的双亲
	T _val;
	int _bf; // 该节点的平衡因子
};

• AVL树的旋转

（1）左单旋：新节点插入较高右子树的右侧。左旋示意图如下：

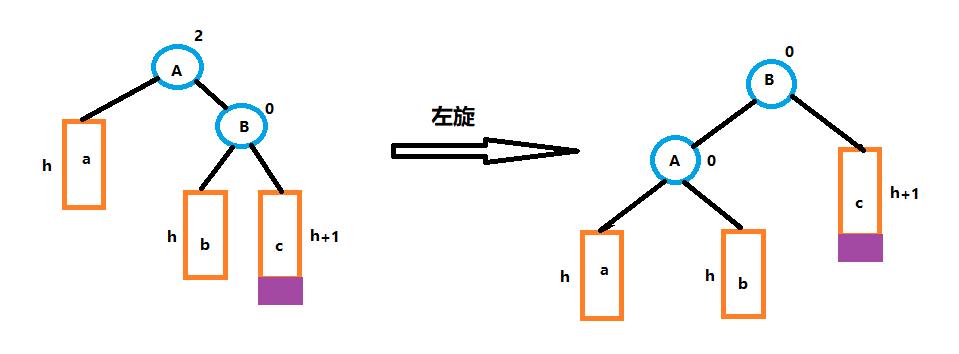
创建subR，subRL，parent，pparent节点，根据图解

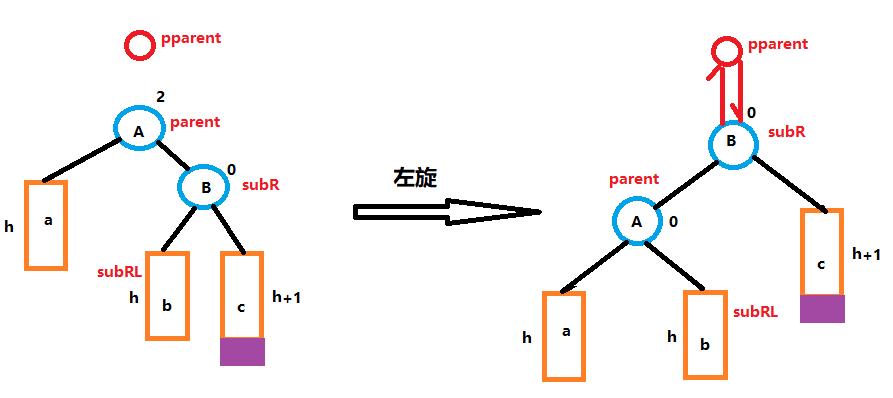
代码如下

void RotateL(Node* parent)//左旋
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		subR->_left = parent;
		parent->_right = subRL;

		if (subRL)
		{
			subRL->_parent = parent;
		}
		if (parent == _root)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			//subR链接在父亲的父亲
			Node* pparent = parent->_parent;
			if (pparent->_left == parent)
				pparent->_left = subR;
			else
				pparent->_right= subR;

			subR->_parent = pparent;
		}
        //更新subR位置到父亲的父亲上
		parent->_parent = subR;

		subR->_bf = parent->_bf = 0;
	}

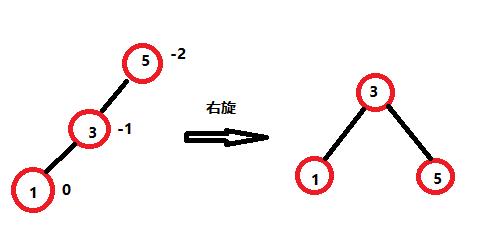
（2）右单旋：新节点插入较高左子树的左侧。右旋示意图如下：

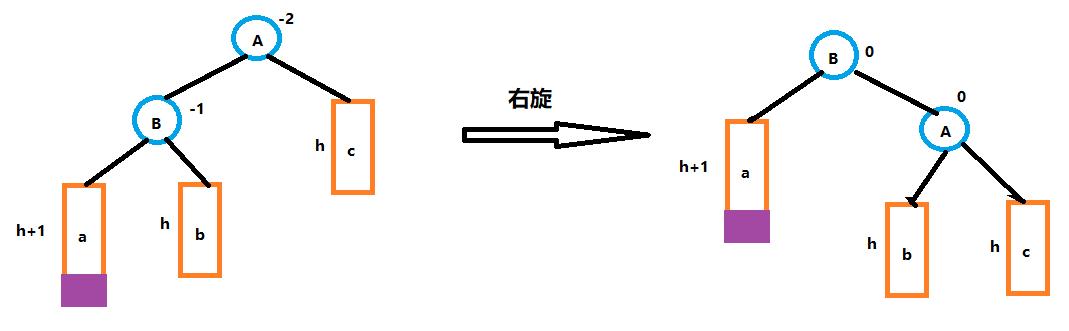
创建subL，subLR，parent，pparent节点，根据图解

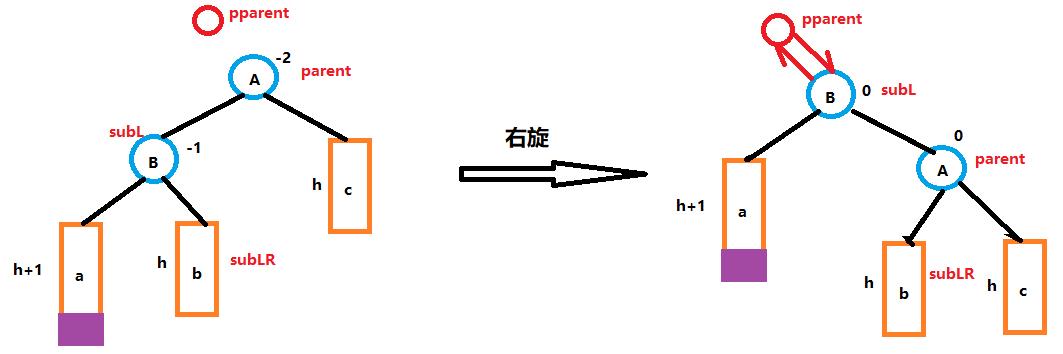
代码如下

void RotateR(Node* parent)//右旋
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		subL->_right = parent;
		parent->_left = subLR;

		if (subLR)
		{
			subLR->_parent = parent;
		}
		if (parent == _root)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			//subL链接在父亲的父亲
			Node* pparent = parent->_parent;
			if (pparent->_left == parent)
				pparent->_left = subL;
			else
				pparent->_right = subL;
			subL->_parent = pparent;
		}
        //更新subL位置到父亲的父亲上
		parent->_parent = subL;

		subL->_bf = parent->_bf = 0;
	}

（3）左右双旋：新节点插入较高左子树的右侧

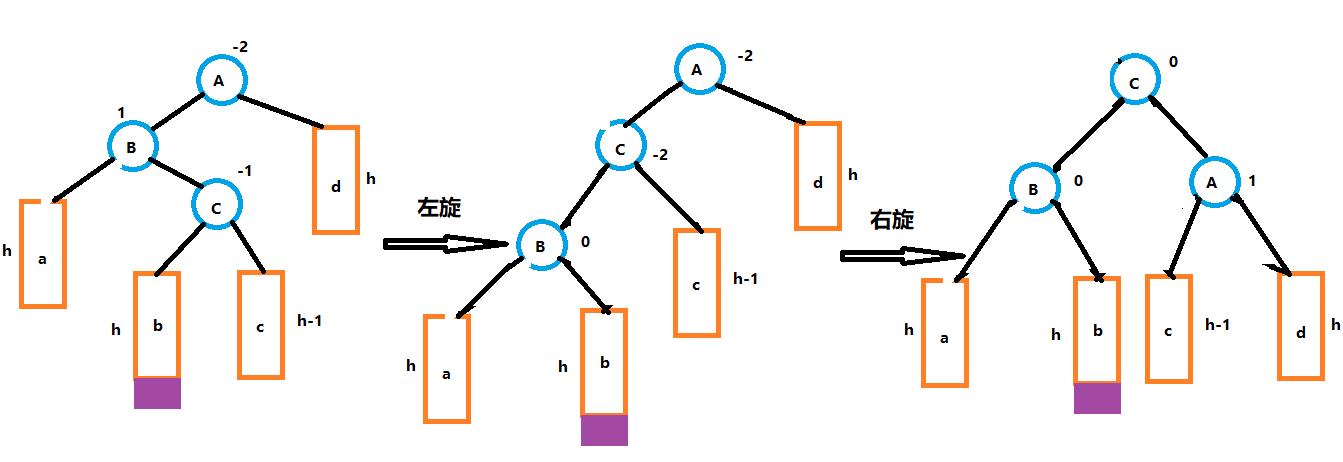
（4）右左双旋：新节点插入较高右子树的左侧

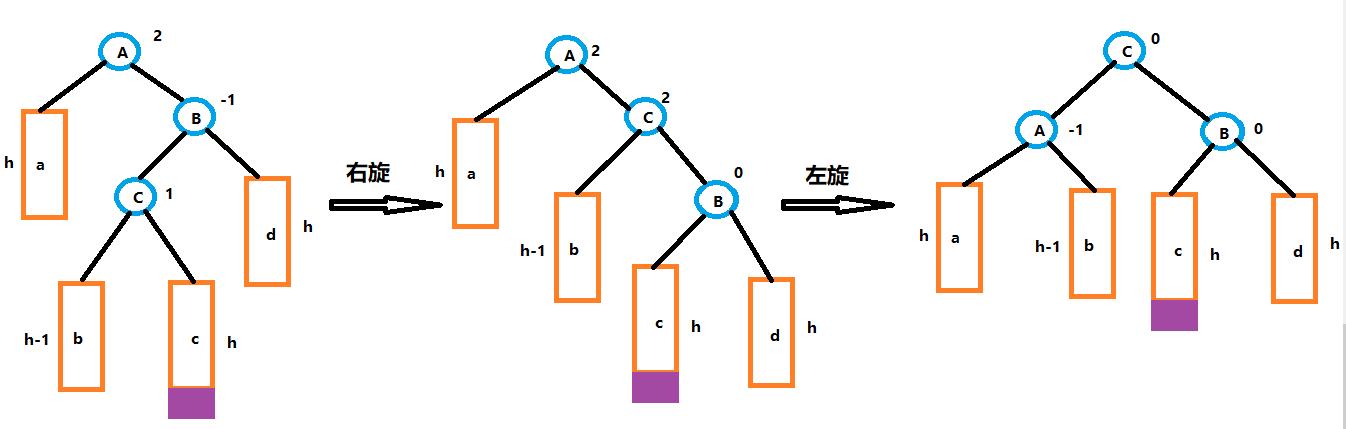
• AVL树的插入

1. 先搜索，直至找到合适位置
2. 选择插入
3. 调整结构及平衡因子

bool insert(const T& val)
	{
		if (_root == nullptr)
		{
			_root = new Node(val);
			return true;
		}
		//搜索
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			parent = cur;//更新父节点
			if (cur->_val == val)
				return false;
			else if (cur->_val < val)
			{
				cur = cur->_right;
			}
			else
				cur = cur->_left;
		}
		//插入
		cur = new Node(val);
		if (parent->_val > val)
		{
			parent->_left = cur;
		}
		else
			parent->_right = cur;

		cur->_parent = parent;
		while (parent)
		{
			//高度 调整平衡因子
			if (parent->_left == cur)//左边增加
				--parent->_bf;
			else
				++parent->_bf;
			if (parent->_bf == 0)  //平衡因子达到0   说明此时对于该父节点，其子树较短的一侧被补齐 ，则停止更新
				//停止更新
				break;
			else if (parent->_bf == 1 || parent->_bf == -1)
				//继续向上更新
			{
				cur = parent;
				parent = parent->_parent;
			}
			else if (abs(parent->_bf) == 2)
			{
				if (parent->_bf == -2&&cur->_bf==-1)
					RotateR(parent);
				else if(parent->_bf == 2&&cur->_bf==1)
					RotateL(parent);
				else if (parent->_bf == -2 && cur->_bf == 1) //左边比右边高  bf=右-左
				{
					Node* subLR = cur->_right;
					int bf = subLR->_bf;
					RotateL(cur);
					RotateR(parent);
					if (bf == 1)
					{
						cur->_bf = -1;
						parent->_bf = 0;
					}
					else if (bf == -1)
					{
						cur->_bf = 0;
						parent->_bf = 1;
					}
				}
				else if (parent->_bf == 2 && cur->_bf == -1) //右边比左边高  bf=右-左
				{
					//保存右左双旋平衡因子
					Node* subRL = cur->_left;
					int bf = subRL->_bf;
					RotateR(cur);
					RotateL(parent);
					
					//修正平衡因子
					if (bf == 1)
					{
						cur->_bf = 0;
						parent->_bf = -1;
					}
					else if(bf==-1)
					{
						cur->_bf = 1;
						parent->_bf = 0;
					}
				}
				break;
			}
		}
		return true;
	}

• 根据平衡因子计算结果：右子树高度-左子树高度

1. 如果新加入节点在父节点的左侧，即左侧高度增加，平衡因子减一
2. 如果新加入节点在父节点的右侧，即右侧高度增加，平衡因子加一

• 当父节点平衡因子为1或-1继续更新，直至平衡因子达到0   说明此时对于该父节点，其子树较短的一侧被补齐 ，则停止更新
• 如果平衡因子调整过程中发现：父节点的平衡因子如果达到-2或2时，说明此时结构存在问题需要调整结构：

1. parent->_bf == -2&&cur->_bf==-1   右旋
2. parent->_bf == 2&&cur->_bf==1    左旋
3. parent->_bf == -2 && cur->_bf == 1  左右双旋
4. parent->_bf == 2 && cur->_bf == -1   右左双旋

• 左右双旋过程，修正平衡因子

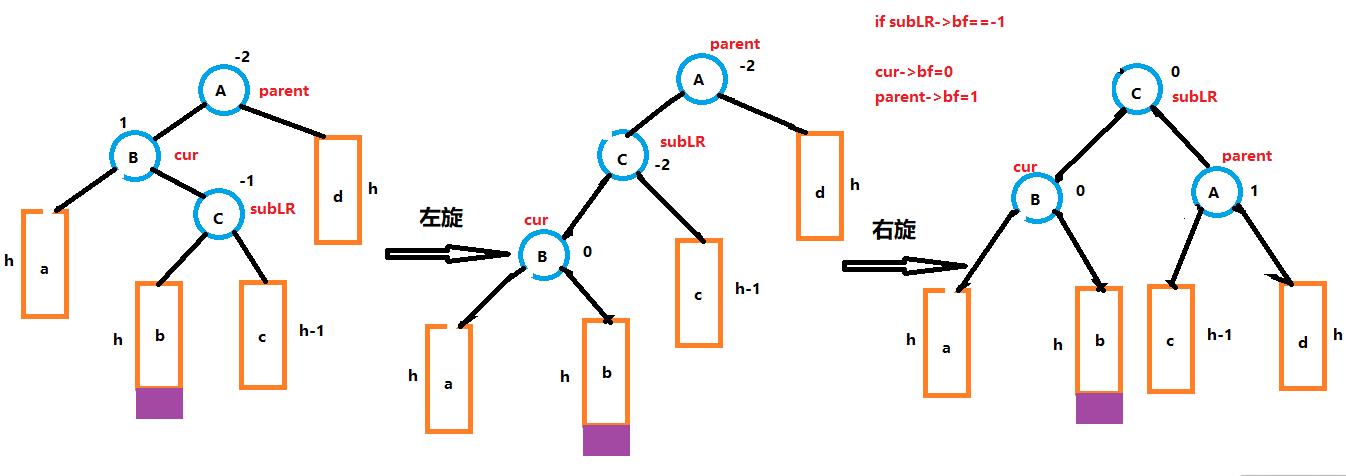
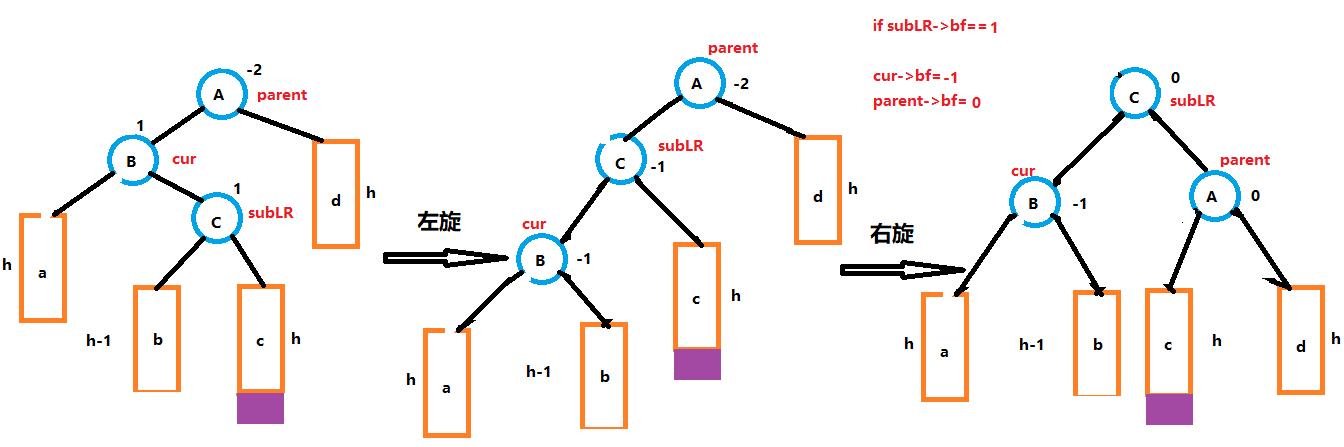
• 右左双旋过程，修正平衡因子

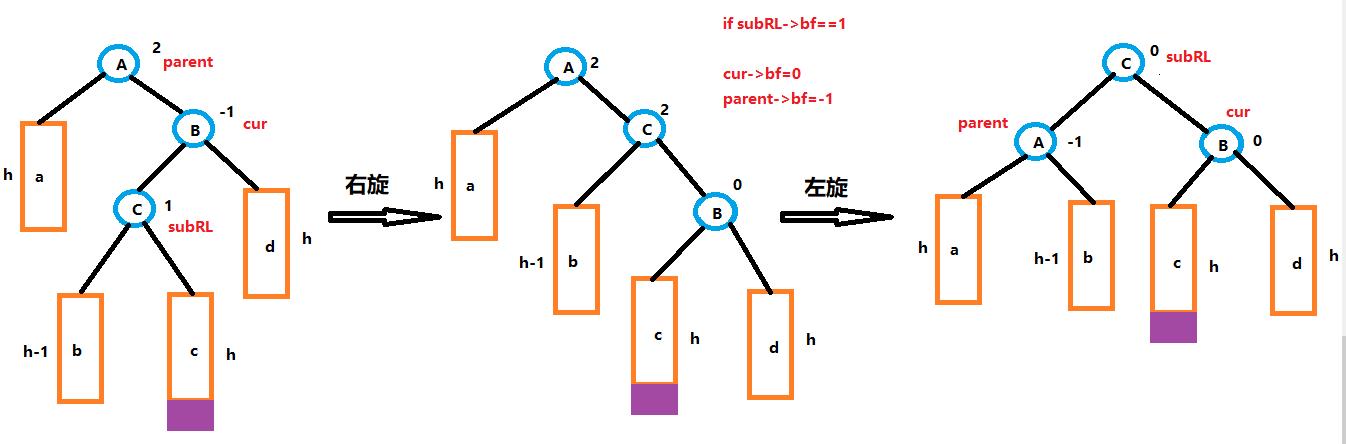
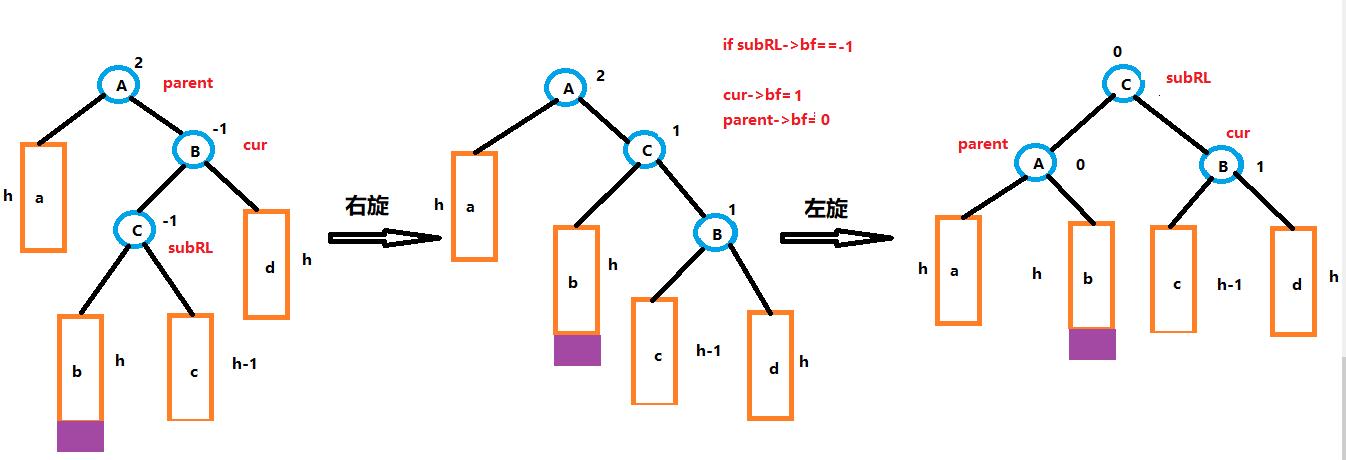
• 代码测试：

（1）顺序插入5 3 1，当1插入后触发右旋

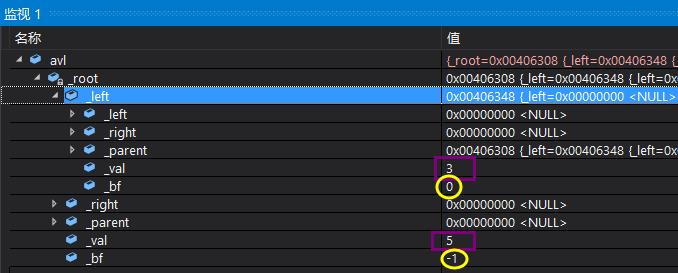
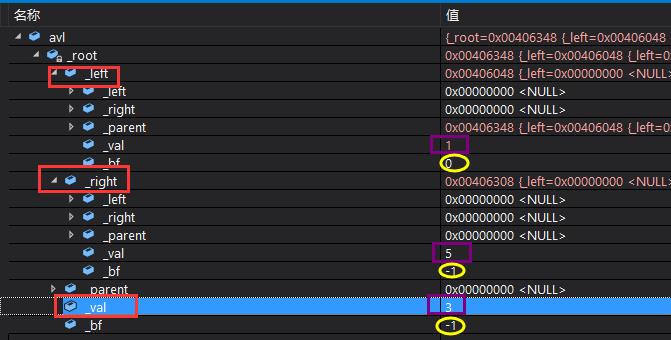
（2）测试随机生成数插入，构建AVL树

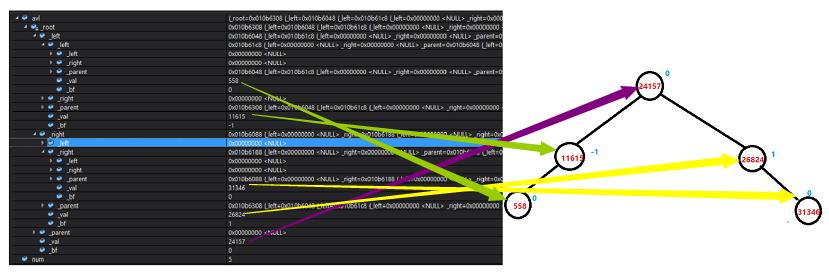
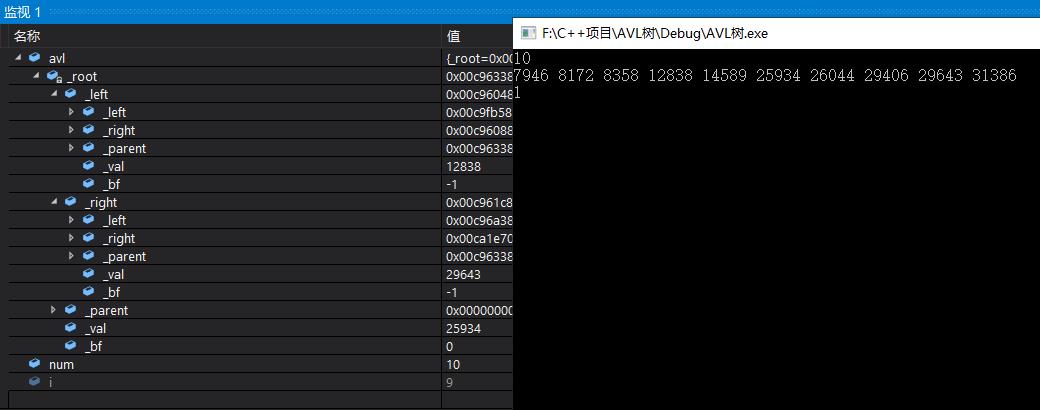
（3）随机10个数，其经过结果变换和平衡因子调整为一棵AVL树

判断所构建的AVL树是否平衡

int Height(Node* root)
	{
		if (root == nullptr)
			return 0;
		int left = Height(root->_left);
		int right = Height(root->_right);
		return left > right ? left + 1 : right + 1;
	}
	bool is_balance()
	{
		return is_balance(_root);
	}
	bool is_balance(Node* root)
	{
		if (root == nullptr)
		{
			return true;
		}

		int left = Height(root->_left);
		int right = Height(root->_right);
		if (right - left != root->_bf)
		{
			cout << "No AVL Tree" << endl;
			return false;
		}
		return abs(root->_bf) < 2 && is_balance(root->_left) && is_balance(root->_right);
	}