二叉排序树学习构建方式及如何遍历二叉排序树

Posted 2021-07-16 踩踩踩从踩

前言

在分析treemap时，分析到了红黑树，而红黑树是由二叉排序树变体产生的，因此学习二叉排序树是常用树的基础；本篇文章主要分析二叉排序树的构建 ，及原理解析，遍历方式。

定义

• 若左子树不为空，则左子树上所有结点的值小于根节点
• 若右子树不为空，则右子树上所有节点的值大于根节点
• 左右子树均为二叉排序树
• 没有重复值，在应用的情况，是不存在，一般都会覆盖掉

定义一个节点 属性包括 

  public static class TreeNode{
        int  data;
        TreeNode leftChild;
        TreeNode rightChild;
        TreeNode parent;
        public TreeNode(int data){
            this.data=data;
            this.leftChild=null;
            this.rightChild=null;
            this.parent=null;
        }
    }

由下图来看看 一个正常的二叉排序树

添加节点

添加这一部分数据 为 5 2 7 3 4 8 6

 

代码实现

 /**
     * 添加节点
     */
    public TreeNode put(int data){
         //插入节点为根节点
        if(root==null){
            TreeNode node=new TreeNode(data);
            root=node;
            return node;
        }
        TreeNode parent=null;
        TreeNode node=root;
        //找到要放入的位置  遍历查找  并记录父节点 ，用于后面插入 
        while(node!=null){
            parent=node;
            if(data<node.data){
                node=node.leftChild;
            }else if(data>node.data){
                node=node.rightChild;
            }else{//是重复值 就不理会了
                return node;
            }
        }
        //生成一个节点放入 判断 左右节点
        TreeNode newNode=new TreeNode(data);
        if(data<parent.data) {
            parent.leftChild = newNode;
        }else{
            parent.rightChild=newNode;
        }
        newNode.parent=parent;

        return newNode;
    }

生成一个二叉排序树；实现点在于 如何去查找需要插入的节点

查询节点

这个从头开始进行向下遍历，对比当前节点和值的大小判断，查询左子树 或者右子树

代码实现

    public TreeNode searchNode(int data){
        if(root==null){
            return null;
        }
        TreeNode node=root;
        while(node!=null){
            if(node.data==data){
                return node;
            }else if(data>node.data){
                node=node.rightChild;
            }else if(data<node.data){
                node=node.leftChild;
            }
        }
        return null;
    }

查找节点 更比较简单 利用的也是while 进行遍历节点

删除节点

删除节点 有一下几种情况

            //先得到父亲，方便后面的操作
            TreeNode parent=node.parent;

• 节点是叶子 ，则直接删除，进行遍历

//1.叶子
            if(node.leftChild==null && node.rightChild==null){
                //特别的情况:1.树上只有一个节点或是空树
                if(parent==null){
                    root=null;
                }else if(parent.rightChild==node){
                    parent.rightChild=null;
                }else if(parent.leftChild==node){
                    parent.leftChild=null;
                }
                node.parent=null;
            }

 

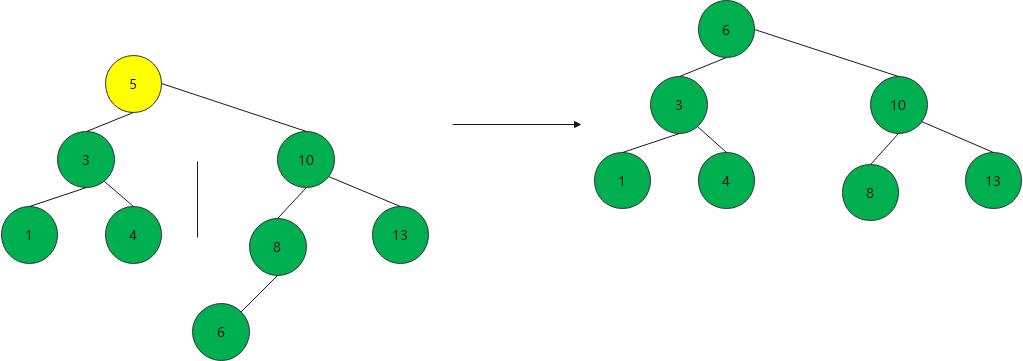
• 当前节点只有左孩子， 判断是 当前节点是父节点的左孩子，还是右孩子，如果是左孩子，则父节点的左孩子设置为左孩子；如果是右孩子，则父节点的右孩子设置为右孩子

 

else if(node.leftChild!=null && node.rightChild==null){
                //2.只有左孩子
                if(parent==null){//如果要删除的是根
                    node.parent=null;
                    node.leftChild.parent=null;
                    root=node.leftChild;
                }else{
                    if(parent.leftChild==node){//要删除的节点是父亲的左边
                        node.leftChild.parent=parent;
                        parent.leftChild=node.leftChild;

                    }else{//要删除的节点是父亲的右边
                        node.leftChild.parent=parent;
                        parent.rightChild=node.leftChild;
                    }
                    node.parent=null;
                }

            }

  

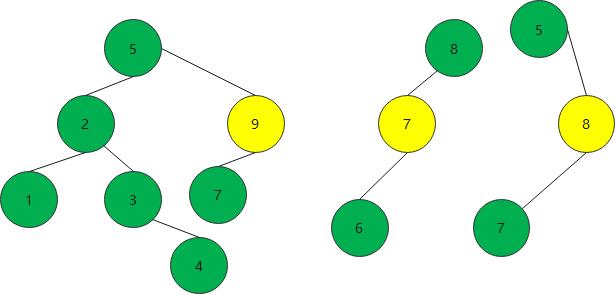
• 只有右孩子的，和左孩子是一样的操作

else if(node.leftChild==null && node.rightChild!=null){
                //3.只有右孩子
                if(parent==null){//如果要删除的是根
                    node.parent=null;
                    node.rightChild.parent=null;
                    root=node.rightChild;
                }else{
                    if(parent.leftChild==node){//要删除的节点是父亲的左边
                        node.rightChild.parent=parent;
                        parent.leftChild=node.rightChild;
                    }else{//要删除的节点是父亲的右边
                        node.rightChild.parent=parent;
                        parent.rightChild=node.rightChild;
                    }
                    node.parent=null;
                }
            }

 

 

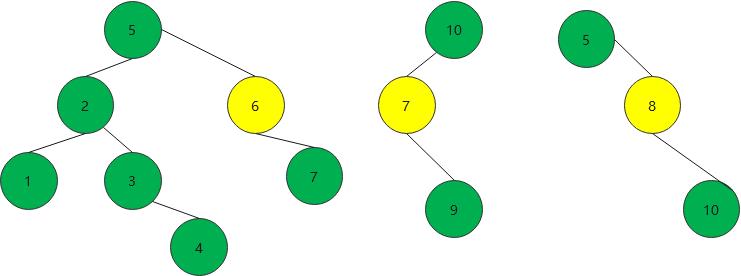
• 有左右两个孩子的 ，如果被删除节点的右子树的左子树为空，就直接补上右子树  ，否则就要补上右子树的左子树上最小的一个

if(node.rightChild.leftChild==null){//1.如果被删除节点的右子树的左子树为空，就直接补上右子树
                    node.rightChild.leftChild=node.leftChild;
                    if(parent==null){
                        root=node.rightChild;
                    }else{
                        if(parent.leftChild==node){
                            parent.leftChild=node.rightChild;
                            //
                        }else{
                            parent.rightChild=node.rightChild;
                            //
                        }
                    }
                    node.parent=null;
                }

 

• 补上右子树的左子树上最小的一个

else{//2.否则就要补上右子树的左子树上最小的一个
                    TreeNode leftNode=getMinLeftTreeNode(node.rightChild);
                    //1
                    leftNode.leftChild=node.leftChild;
                    //2
                    TreeNode leftNodeP=leftNode.parent;
                    leftNodeP.leftChild=leftNode.rightChild;
                    //3
                    leftNode.rightChild=node.rightChild;
                    //4
                    if(parent==null){
                        root=leftNode;
                    }else{
                        if(parent.leftChild==node){
                            parent.leftChild=leftNode;
                            //
                        }else{
                            parent.rightChild=leftNode;
                            //
                        }
                    }
                }


    private TreeNode getMinLeftTreeNode(TreeNode node) {
        TreeNode curRoot=null;
        if(node==null){
            return null;
        }else{
            curRoot=node;
            while(curRoot.leftChild!=null){
                curRoot=curRoot.leftChild;
            }
        }
        return curRoot;
    }

不断遍历寻找到 删除节点右子树上左子树最小的点进行替换删除的点

 

遍历节点

采用中序遍历的方式

  public void midOrderTraverse(TreeNode root){
        if(root==null){
            return;
        }
        //LDR
        midOrderTraverse(root.leftChild);
        System.out.print(root.data+" ");
        midOrderTraverse(root.rightChild);
    }

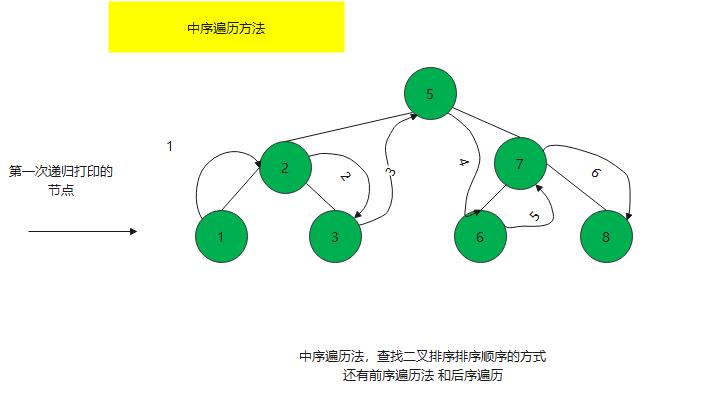
对于二叉排序树来说，用中序来遍历是能做顺序遍历，利用递归的方式进行实现中序遍历 是最简单的， 

利用 先遍历左边知道为空时，才返回打印最左边节点，在查看最左边节点右孩子肯定不存，就往上走，打印数据，在往右孩子走；以此类推，利用递归的特性

前序遍历法

public void traverse(TreeNode root){
        if(root==null){
            return;
        }
        System.out.print(root.data+" ");
        traverse(root.leftChild);
        traverse(root.rightChild);
    }

 

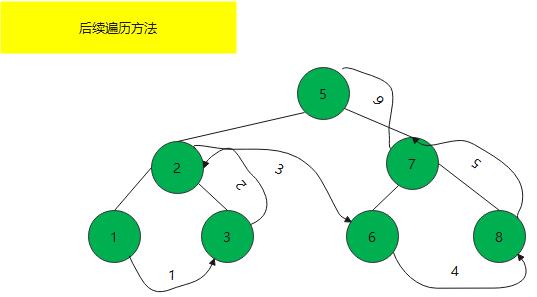
后序遍历法

public void traverse(TreeNode root){
        if(root==null){
            return;
        }
        
        traverse(root.leftChild);
        traverse(root.rightChild);
        System.out.print(root.data+" ");
    }

总结

整个二叉排序树比较经典，也是我们在应用比较广泛，比如 在此基础上做了变体  avl树，红黑树等等；所以也需要我们充分理解 二叉排序树，才能继续理解红黑树等比较复杂的树