哈希表与树的介绍

Posted 2021-07-16 踩踩踩从踩

前言

该篇文章，主要带我们认识什么哈希表和树，为我们在研究各个数据结构的实现及扩展算法，有个基本的认识。

哈希表

特点

• 数组  ：寻址容易  ；数据连续存储空间
• 链表：插入与删除容易 ；放在堆内存中对象，存储并不连续
• 哈希表：寻址容易，插入删除也容易的数据结构；一般采用数组加链表的格式

hashtable 

哈希表（Hash table，也叫散列表）
是根据关键码值(Key value)而直接进行访问的数据结构，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。

关键码值(Key value)也可以当成是key的hash值  ,这个映射函数叫做散列函数;存放记录的数组叫做散列表

hashtable例子

Key : {14, 19, 1, 7, 31, 13, 0, 18} 散列表: 大小为13 的数组 a[13]; 散列函数: f(x) = x mod 13;   

通过上面的展示去了解到整个hash表是什么.

缺点

扩容需要消费大量的空间和性能，因为需要重新计算数据的hash，因此整个散列表设置 容量大小 是相当重要的

应用

电话号码，字典，点歌系统，QQ，微信的好友等，以及缓存等，从jdk1.8以后从扩展的 putIfAbsent 方法 都是有利于我们实现缓存操作的

设计：拉链法

jdk1.8以前

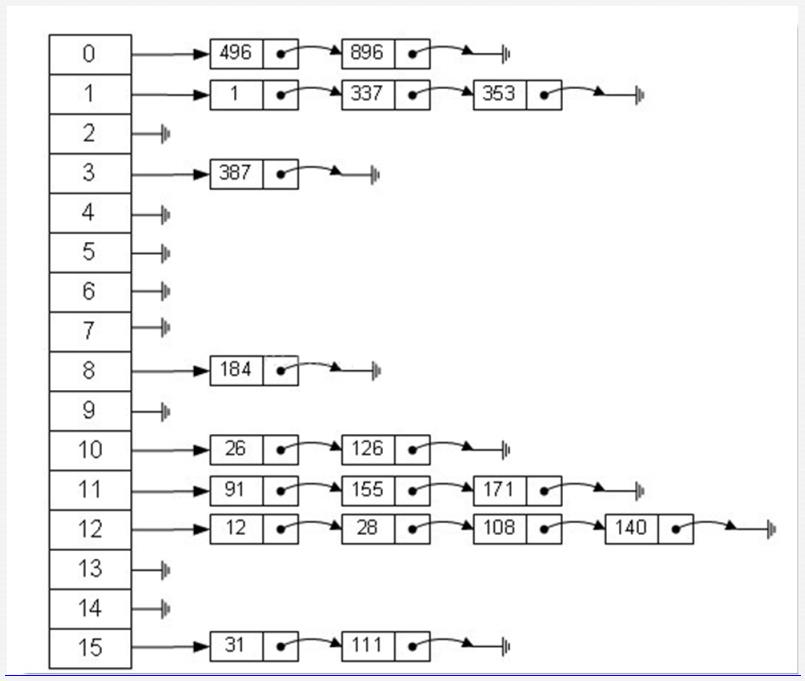
整个散列表的实现，只要有hash 碰撞 就采用链表的形式进行解决；但链表的访问的时间复杂度是o(n) 的， 并且hash碰撞越大，链表越长，访问效率是很慢的，因此java实现的散列表不断在优化这个

jdk1.8开始 

当链表长度超过阈值，并且 容量达到默认64时，链表就转换成红黑树

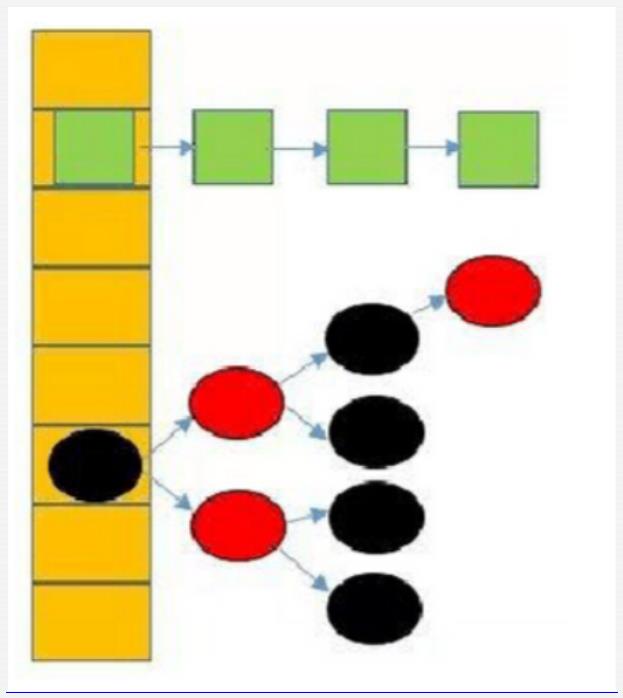
树的概念

什么是树

树（tree） 是n（n>=0）个结点的有限集。n=0时，称为空树。有任意一颗非空树中：（1） 有且仅有一个特定的称为根 root的结点， （2） 当n>1 时，其余结点可分为m(m>0) 个互不相交的有限集， t1 t2  .... tn 其中每个集合也是一颗树，并且称为根的子树

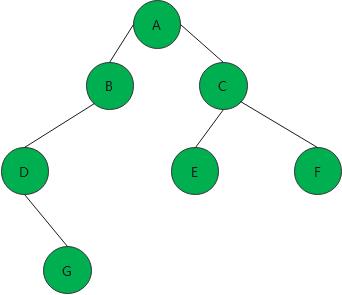
结点与树的度

节点拥有的子树数称为结点的度。度为0的结点称为叶子结点或终端结点，度不为0的结点称为非终端结点或分支结点。除根结点以外，分支结点也称为内部结点，树的度是树内各结点的度的最大值

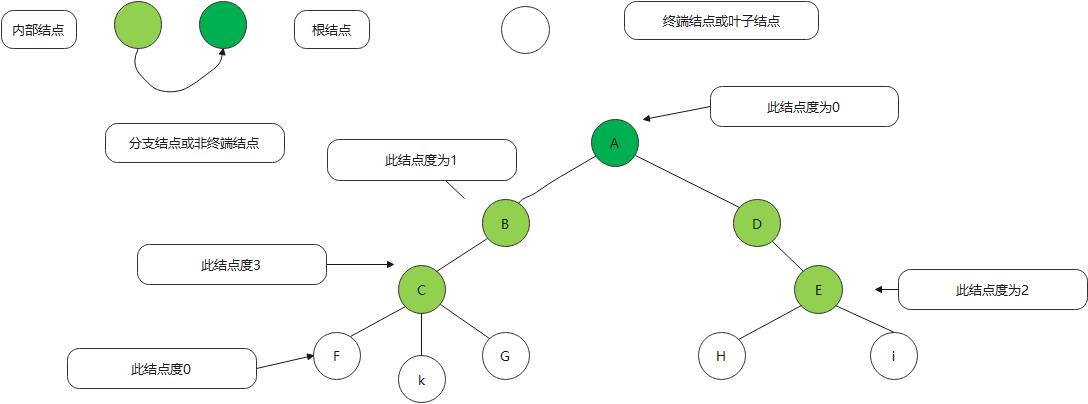
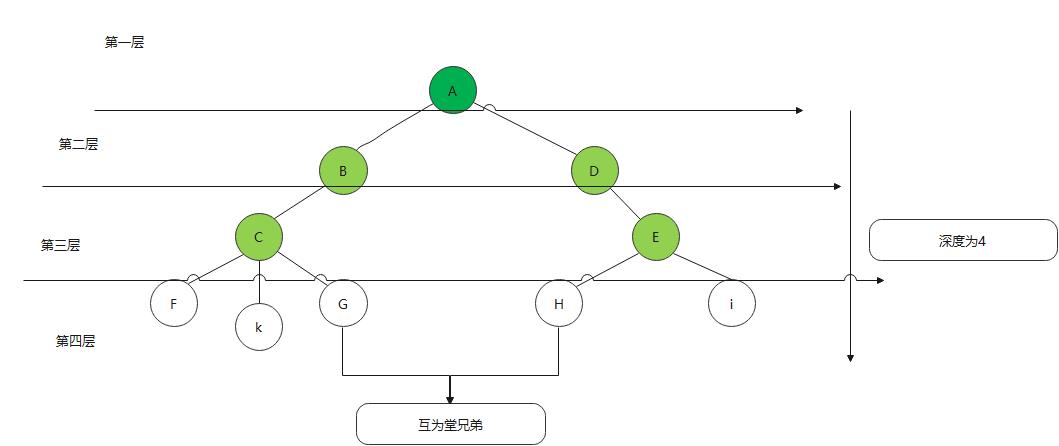
层次与深度

结点的层次（level）从根开始定义起，根为第一层，根的孩子为第二层。若某结点在第一层，则其子树根在l+1层。其双亲在同一层的结点互为堂兄妹。显然f k g h i互为堂兄弟  ce 也是的 。树的结点的最大层次称为树的深度或高度，当前树的深度为4 ，这个概念在我们研究树的情况获得更好的理解

森林

森林（forest） 是m（m>=0）棵不相交的树，多个树组成一森林

树的存储结构

双亲表示法

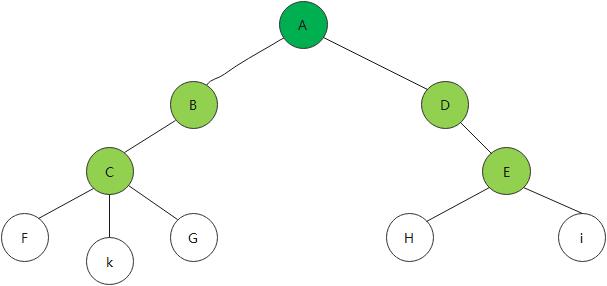
双亲表示法的方式，也就是通过 结点里面记录着父结点.

下标	data	parent
0	A	-1
1	B	0
2	D	0
3	C	1
4	E	2
5	F	3
6	K	3
7	G	3
8	H	4
9	I	4

孩子表示法

通过记录下孩子，来表示树

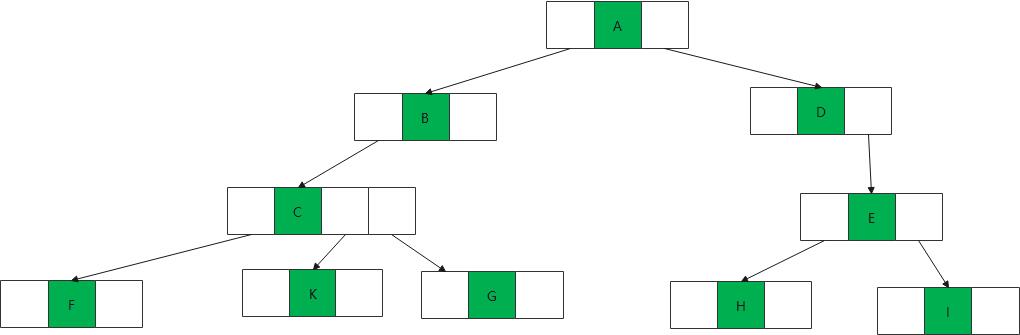
双亲孩子表示法

把每个结点的孩子结点排列起来，以单链表作为存储结构，则n个结点有n个孩子链表，如果是叶子结点则此单链表为空，然后n个头指针又组成一个线性表，采用顺序存储结构，存放在一个一维数组中

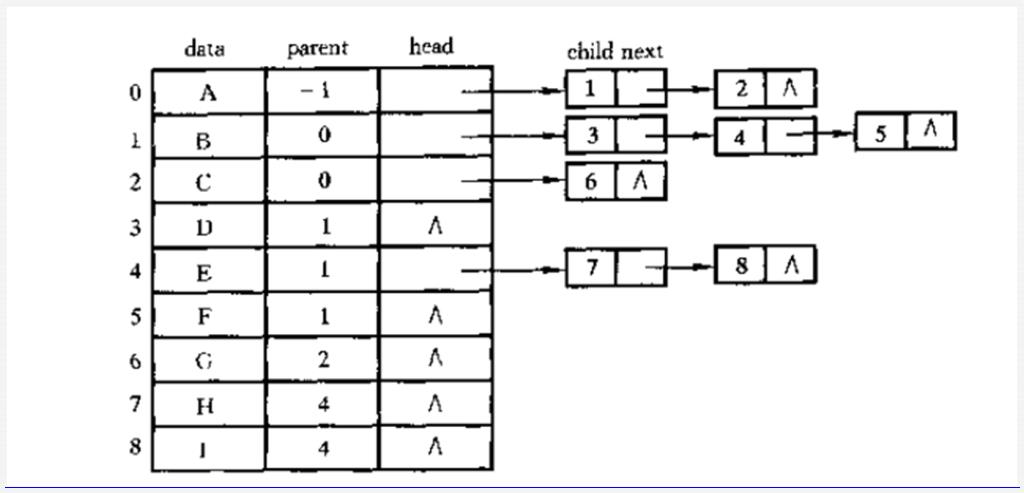
这个是引用的别人图，我就没在画， 把双亲和孩子的存储结构给结合起来

孩子兄弟表示法

孩子兄弟表示法为每个节点设计三个域：一个数据域，一个该节点的第一个孩子节点域，一个该节点的下一个节点的兄弟指针域

 

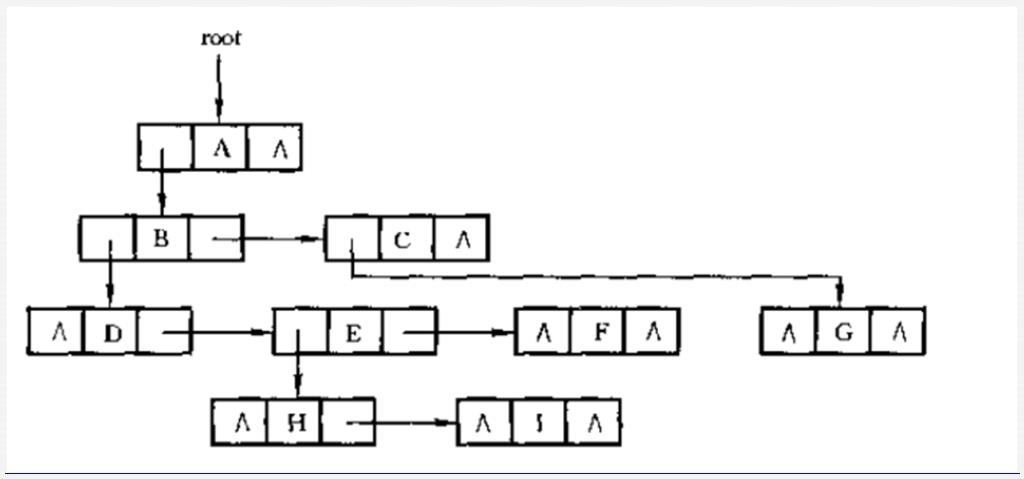
二叉树

二叉树在应用中非常常用，无论avl树，还是红黑树等，都是基于二叉树的

二叉树定义

二叉树（Binary tree）是n(n>=0) 个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两颗互不相交的，分别称为根结点的左子树和右子树的二叉树组成

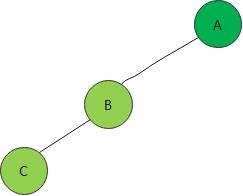
上图是一个斜树

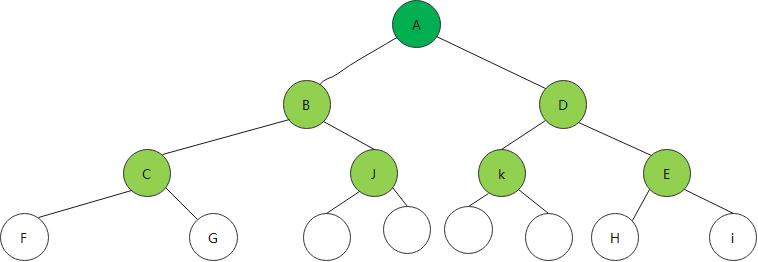
上图为满二叉树，定义为除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。如果一棵二叉树的结点要么是叶子结点，要么它有两个子结点，这样的树就是满二叉树。(一棵满二叉树的每一个结点要么是叶子结点，要么它有两个子结点，但是反过来不成立，因为完全二叉树也满足这个要求，但不是满二叉树)

 

完全二叉树 ，定义 一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树 ；

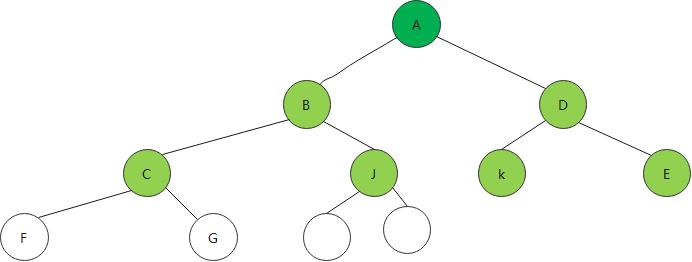
一颗深度为k,且有2的k次方-1个结点的二叉树称为满二叉树。

如果对满二叉树的结点进行编号, 约定编号从根结点起, 自上而下, 自左而右。则深度为k的, 有n个结点的二叉树, 当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时, 称之为完全二叉树

从满二叉树和完全二叉树的定义可以看出, 满二叉树是完全二叉树的特殊形态, 即如果一棵二叉树是满二叉树, 则它必定是完全二叉树

二叉树存储结构

顺序存储，采用数组的存储方法 也就是堆 2n+1 2n+2

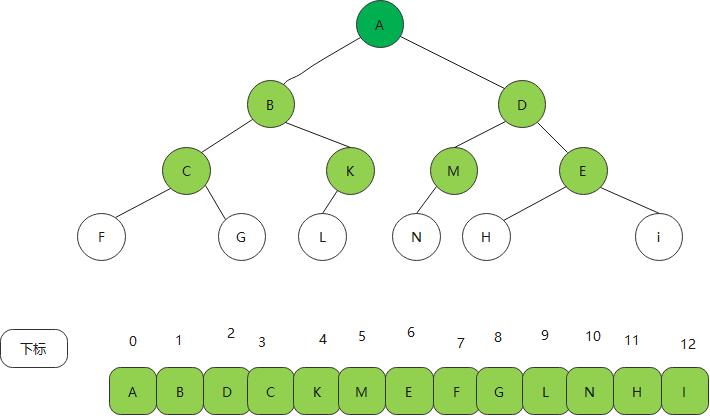
链式存储

 

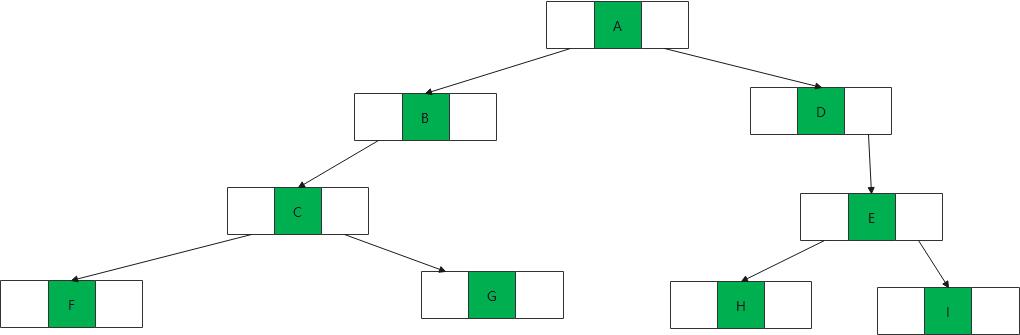
二叉树的遍历

采用中序遍历的方式(LDR)

  public void midOrderTraverse(TreeNode root){
        if(root==null){
            return;
        }
        //LDR
        midOrderTraverse(root.leftChild);
        System.out.print(root.data+" ");
        midOrderTraverse(root.rightChild);
    }

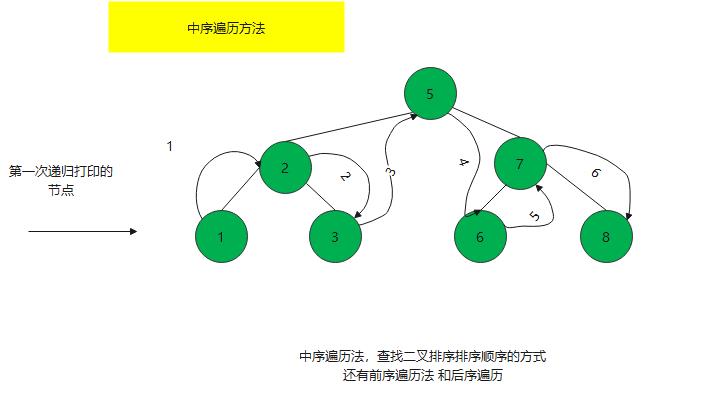
对于二叉排序树来说，用中序来遍历是能做顺序遍历，利用递归的方式进行实现中序遍历 是最简单的， 

规则是若树为空，则空操作返回，否则从根结点开始（注意并不是先访问根结点），
中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树

利用 先遍历左边知道为空时，才返回打印最左边节点，在查看最左边节点右孩子肯定不存，就往上走，打印数据，在往右孩子走；以此类推，利用递归的特性

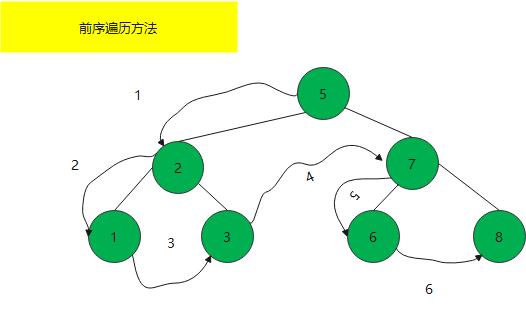
前序遍历法(DLR)

规则是若二叉树为空，则空操作返回，否则先访问跟结点，然后前序遍历左子树，再前序遍历右子树

public void traverse(TreeNode root){
        if(root==null){
            return;
        }
        System.out.print(root.data+" ");
        traverse(root.leftChild);
        traverse(root.rightChild);
    }

 

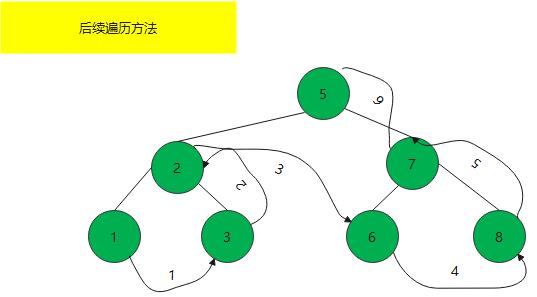
后序遍历法(LRD)

规则是若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后是访问根结点

public void traverse(TreeNode root){
        if(root==null){
            return;
        }
        
        traverse(root.leftChild);
        traverse(root.rightChild);
        System.out.print(root.data+" ");
    }