分治法应用之二分查找 快速排序递归排序

Posted 2021-07-16 踩踩踩从踩

前言

我们都知道在常用的五大常用的经典算法：分治算法、贪心算法、动态规划算法、回溯算法、分支界限算法、每个算法在计算机科学中都有很重要的地位；本篇文章会介绍这其中分治算法一种实现 ，包括顺序查找、二分查找、快速排序  、归并排序等方法

定义

分治法的从字面意思来看“分而治之”，就是将一个复杂问题分成两个或者多个相同或相似的子问题，在把子问题分成更小的问题。。。。直到最后子问题可以简单的求解，即子问题的答案就是原问题的答案。各位这样一看看，是不是觉得突然想起某个算法，对，就是递归，或者也许你想起的是归并排序算法，或者二分查找法也好，也并不重要。这个思想就是这些算法的基础,然后我们从小及大来理解这个算法吧

顺序查找

如果线性表为无序表，即表中元素的排列是无序的，则不管线性表采用顺序存储还是链式存储，都必须使用顺序查找。如果线性表有序，则采用链式存储结构，则也必须使用顺序查找的方式

• 这种方式在我们的代码开发种算是最常用的查找方法；
• 例如在LinkedList（链表结构）查找 某个值。 当然在树结构是采用这种方式。
• 下图就是顺序查找的在二叉排序树上的一种体现
•  
• 

二分查找法

前提条件：数据已经排序才能进行二分查找法  数组顺序存储结构

通过上图进行分析到我们二分查找法 查找速率是相当快的，在顺序数组中查找方法，并且时间复杂度只有O(logn) ，也就是说如果你有8个元素，只需要三次就可以查找到；这也是将问题拆分开，问题最小化。

正确的写一个二分查找是比较难的，需要设计成左闭右开结构，是一种区间无重复的思想； random(０，１)等大量的数学函数 for(int i=0;i<array.length;i++） 等中使用

 

我们从一段代码去分解它

 /**
     * 二分查找
     */
    public static int binarySearch(int[] array,int fromIndex,int toIndex,int key){
        int low=fromIndex;
        int high=toIndex-1;
        while(low<=high){
            int mid=(low+high)/2;//取中间
            int midVal=array[mid];
            if(key>midVal){//去右边找
                low=mid+1;
            }else if(key<midVal){//去左边找
                high=mid-1;
            }else{
                return mid;
            }
        }
        return -(low+1);//low+1表示找不到时停在了第low+1个元素的位置
    }

• 首先toIndex -1 ， 是为了左开右闭的区间
• 判断是否结束，则判断low大于high指针
• 取得中间指针  int mid=(low+high)/2  
• int midVal=array[mid]  获得中间指针的数据 
• 判断值大于mid ，low=mid+1;    赋值 
• 这样不断循环就可以快速查找到数据

这样一分析感觉二分查找法很简单，但需要注意左闭右开的区间；并跳出循环的条件

快速排序（前序排序）

快速排序由于排序效率在同为O(N*logN)的几种排序方法中效率较高，并且快速排序思想----分治法也确实实用，我们就来分析快速排序

原理

主要点在于其中一部分的所有数据都比另外一不部分的所有数据都要小，然后再按次方法对这两部分数据分别进行快速排序，整个排序过程可以递归或者非递归进行，以此达到整个数据变成有序序列。

一次快速排序的过程

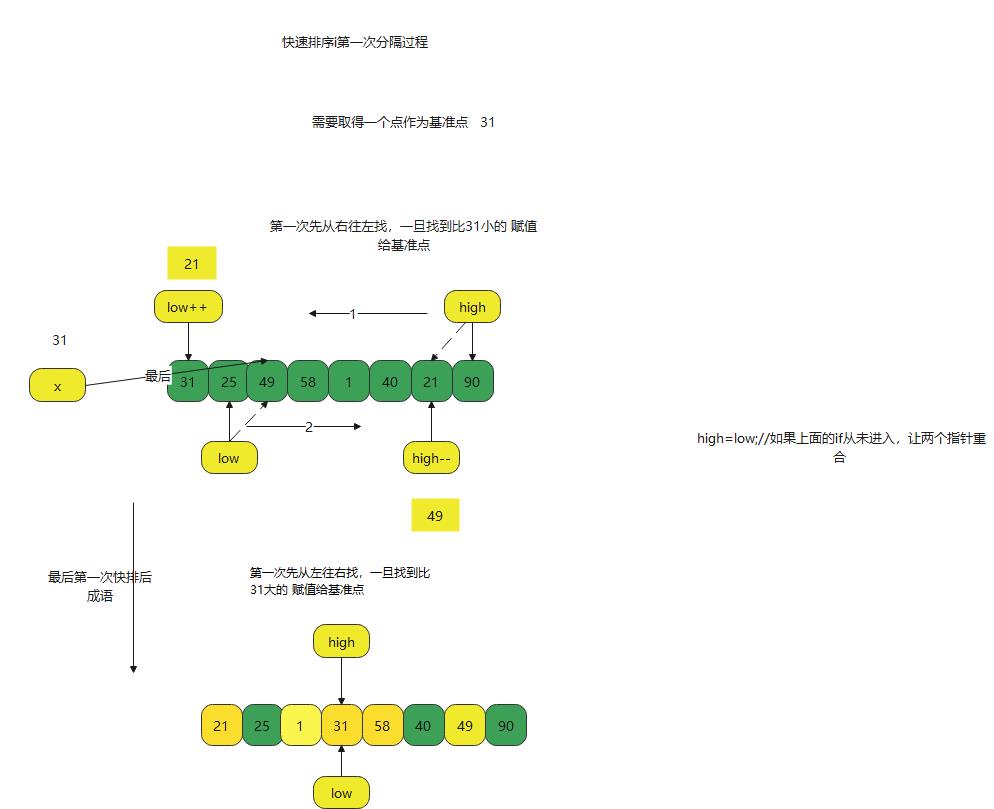
代码分析 一次快排序的过程

 public static void quickSort(int[] array,int begin,int end){
        if(end-begin<=0) return;
        int x=array[begin];
        int low=begin;//0
        int high=end;//5
        //由于会从两头取数据，需要一个方向
        boolean direction=true;
        L1:
        while(low<high){
            if(direction){//从右往左找
                for(int i=high;i>low;i--){
                    if(array[i]<=x){
                        array[low++]=array[i];
                        high=i;
                        direction=!direction;
                        continue L1;
                    }
                }
                high=low;//如果上面的if从未进入，让两个指针重合
            }else{
                for(int i=low;i<high;i++){
                    if(array[i]>=x){
                        array[high--]=array[i];
                        low=i;
                        direction=!direction;
                        continue L1;
                    }
                }
                low=high;
            }
        }
        //把最后找到的值 放入中间位置
        array[low]=x;
        //开始完成左右两边的操作
        quickSort(array,begin,low-1);
        quickSort(array,low+1,end);
    }

• 首先取得  对比的基准点  并 取得开始点，和结束点

if(end-begin<=0) return;
        int x=array[begin];
        int low=begin;//0
        int high=end;//5

• 其次需要记录一个方向，因为在快速排序时，需要左右方法移动排序

        //由于会从两头取数据，需要一个方向
        boolean direction=true;

• 从右往左走 ，只要找到比基准点小的，就 交换到基本点的值，并交换方向

 if(direction){//从右往左找
                for(int i=high;i>low;i--){
                    if(array[i]<=x){
                        array[low++]=array[i];
                        high=i;
                        direction=!direction;
                        continue L1;
                    }
                }
                high=low;//如果上面的if从未进入，让两个指针重合
            }

• 从往左走 ，只要找到比基准点小的，就 交换到基本点的值，并交换方向 

else{
                for(int i=low;i<high;i++){
                    if(array[i]>=x){
                        array[high--]=array[i];
                        low=i;
                        direction=!direction;
                        continue L1;
                    }
                }
                low=high;
            }

• 当low等于 high时，就跳转循环一次快排结束  while(low<high)
• 把最后找到的值 放入中间位置  基准的值

 array[low]=x;

• 开始完成左右两边的操作 

       quickSort(array,begin,low-1);
        quickSort(array,low+1,end);

这就是整个 快排的基本思想及实现，将数据进行分段排序， 但这个 有一个确定， 应用场景 是   数据量大并且是线性结构 ；

短处
  有大量重复数据的时候，性能不好
  单向链式结构处理性能不好（一般来说，链式都不使用）

因此我们用另外一种算法，也是分治法的体现 来排序  （归并排序（后序））

归并排序（后序）

归并排序的思想和快排的思想都是来自分治法，因此思想是很像的，当我们要排序一个数组时，我们首先将这个数组拆分成两半，想办法将这两个子数组进行排序，然后再将这两个有序的子数组合并为一个有序的数组。  这个和快排的差别在于，快排是基于原数组上操作，而归并则需要拆分多个数组

原理

 

实现方式

//合并排序
    public static void mergeSort(int array[],int left,int right){
        if(left==right){
            return;
        }else{
            int mid=(left+right)/2;
            mergeSort(array,left,mid);
            mergeSort(array,mid+1,right);
            merge(array,left,mid+1,right);
        }
    }

    //    0    4   7
    //    1  2  5  9 === 3  4  10  11
    public static void merge(int[] array,int left,int mid,int right){
        int leftSize=mid-left;
        int rightSize=right-mid+1;
        //生成数组
        int[] leftArray=new int[leftSize];
        int[] rightArray=new int[rightSize];
        //填充数据
        for(int i=left;i<mid;i++){
            leftArray[i-left]=array[i];
        }
        for(int i=mid;i<=right;i++){
            rightArray[i-mid]=array[i];
        }
        //合并
        int i=0;
        int j=0;
        int k=left;
        while(i<leftSize && j<rightSize){
            if(leftArray[i]<rightArray[j]){
                array[k]=leftArray[i];
                k++;i++;
            }else{
                array[k]=rightArray[j];
                k++;j++;
            }
        }
        while(i<leftSize){
            array[k]=leftArray[i];
            k++;i++;
        }
        while(j<rightSize){
            array[k]=rightArray[j];
            k++;j++;
        }
    }

• 我们先从拆分开始说起，利用递归的特性做左右不断拆分

   public static void mergeSort(int array[],int left,int right){
        if(left==right){
            return;
        }else{
            int mid=(left+right)/2;
            mergeSort(array,left,mid);
            mergeSort(array,mid+1,right);
            merge(array,left,mid+1,right);
        }
    }

• merge 将拆分后的数据进行生成新的数组，并填充数据

 int leftSize=mid-left;
        int rightSize=right-mid+1;
        //生成数组
        int[] leftArray=new int[leftSize];
        int[] rightArray=new int[rightSize];
        //填充数据
        for(int i=left;i<mid;i++){
            leftArray[i-left]=array[i];
        }
        for(int i=mid;i<=right;i++){
            rightArray[i-mid]=array[i];
        }

• 进行合并数据

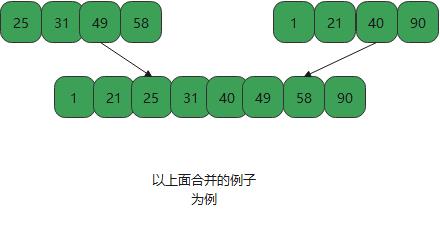
• 代码左右合并排序

  //合并
        int i=0;
        int j=0;
        int k=left;
        while(i<leftSize && j<rightSize){
            if(leftArray[i]<rightArray[j]){
                array[k]=leftArray[i];
                k++;i++;
            }else{
                array[k]=rightArray[j];
                k++;j++;
            }
        }

当leftArray[i]>rightArray[j]

当leftArray[i]<rightArray[j]

这样分成最小化合并排序

• 最后需要参考最小化进行补位

 while(i<leftSize){
            array[k]=leftArray[i];
            k++;i++;
        }
        while(j<rightSize){
            array[k]=rightArray[j];
            k++;j++;
        }

这样一个完整的归并排序就完成了

• 归并排序的应用场景

         数据量大并且有很多重复数据，链式结构

•   短处

        需要空间大

 

总结

整个分治法的应用在整个算法中占了很大一部分，这里二分查找法，快排，以及归并排序，都是分治法的应用，但现实编程中，并不局限于这个。