栈的特点及其实例 递归 阶乘 斐波拉契数列等的应用详解

Posted 2021-07-16 踩踩踩从踩

前言

栈是一种受限的线性表结构，因此我们就应该知道他的表现形式也应该有顺序结构和链式结构，它有什么特点 及其应用，在这篇文章会重点介绍

什么是栈

栈只要不是初学者都应该知道把，栈又名堆栈，它是一种线性表结构；和线性表并没差别，区别在于更多限制

特性

栈是限定仅在表尾进行插入和删除操作的线性表

她允许插入和删除的一端称为栈顶 top,而另一端称为栈底，而中间叫栈体，不含任何元素的栈叫做空栈，栈又称为后进先出的线性表

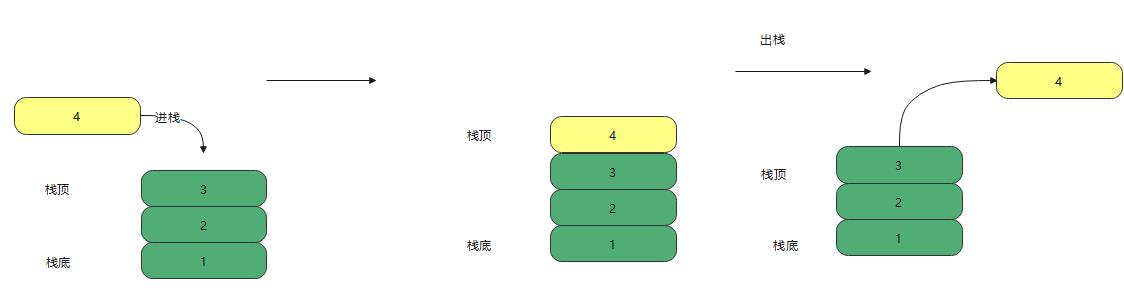
由于栈的特殊性，因此进栈的数据是1234  的顺序，但出栈的顺序是4321

先进后出的顺序 也就是说栈

实现

栈的实现有两种 顺序结构（包括循环数组的结构）和链式存储

顺序结构实现

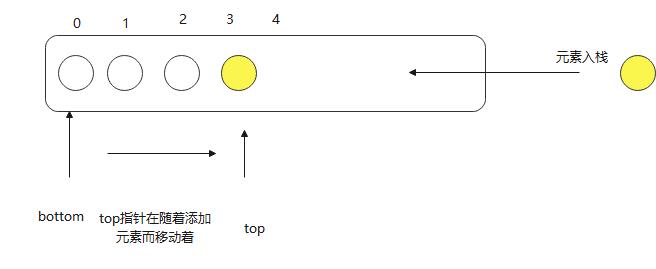
而在应用中 jdk中stack 就是基本栈的基本实现，利用elementCount指针(top指针)控制数据的取出

Java 集合深入理解 （五） ：stack源码分析，及如何利用vector实现栈

jdk早已不推荐stack类，还是因为是vector实现的，所以作者推荐ArrayDeque实现栈，利用循环数组来实现  有head指针(top) 和tail指针（bottom） 共同控制

Java 集合深入理解 （十三） ：ArrayDeque实现原理研究，及动态扩容、双端队列和单队列和栈比较

顺序结构 的栈是非常容易的

链式结构的实现

实现原理

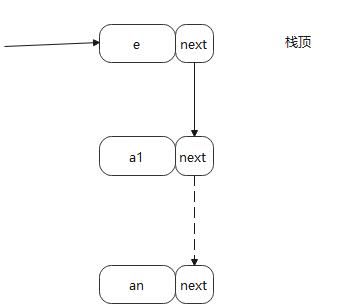
把栈顶放到里面，节点的next 栈顶指针，往下添加， 我们要取得肯定是取top指针

利用栈 ，我们可以将数据进行倒序，也就是 比如123456 如何 进行倒序  放到  栈中，取得适合 进行倒序就行 这个top指针 一定是不断添加值在变化得

这个栈得特性才有了倒序

逆波兰表达式

我们都知道在jvm虚拟机规范里面 规定线程私有区域里面 jvm虚拟机栈 里面操作数栈就是用于做操作计算，例如  a/2   a*2 a+2 等等， 所以为什么位应算得效率是最高得。

标准四则运算表达式—中缀表达式
9+(3-1)X3+10/2    20
计算机采用—后缀表达式
9 3 1 - 3 * + 10 2 / +   20

中缀表达式转换成后缀表达式

下图中横向表示栈顶，竖向表示取到的操作符

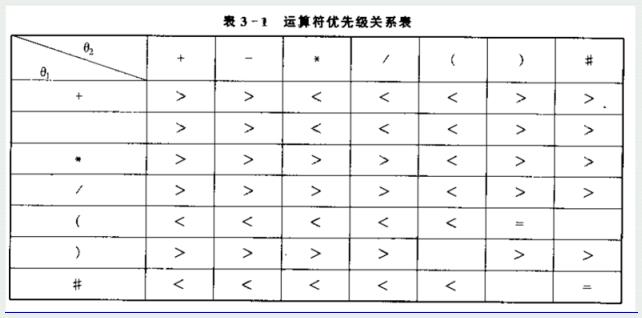
按数学的计算法则，+的优先级是等于-的，但是逆波兰的优先级，则是不相等的，栈顶和取到操作数栈的符号进行对比

然后进行 数字输出，运算符进栈，括号匹配出栈，比栈顶优先级低就出栈（表中1>2）

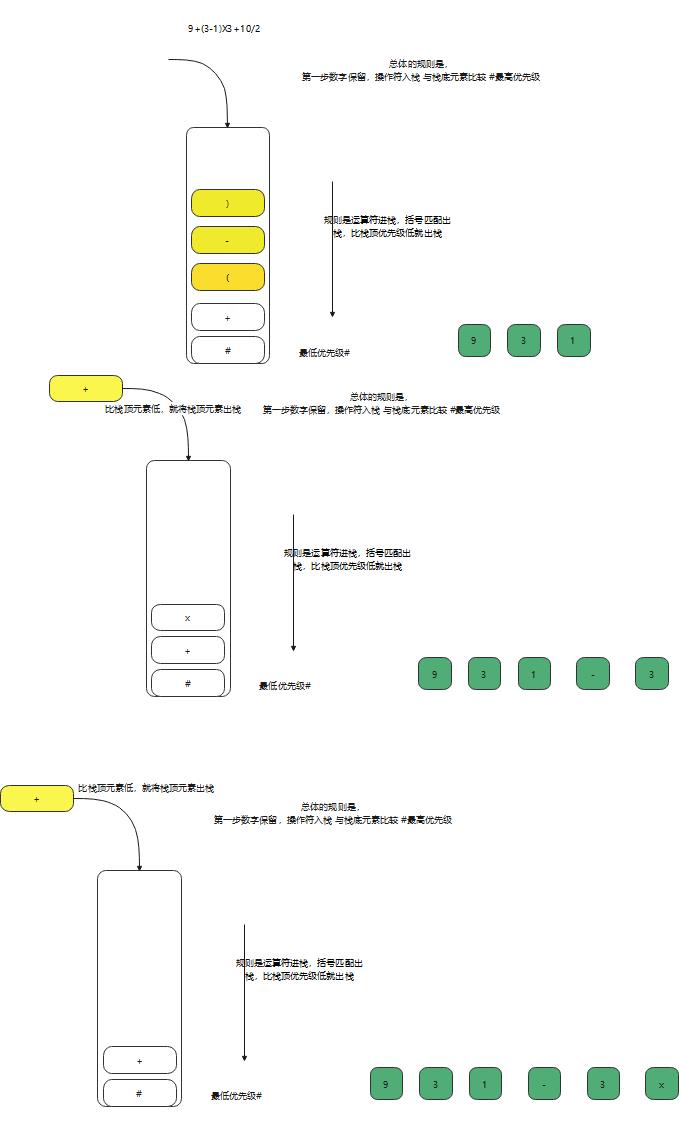
最后得出保存下面的后缀表达式 数据 

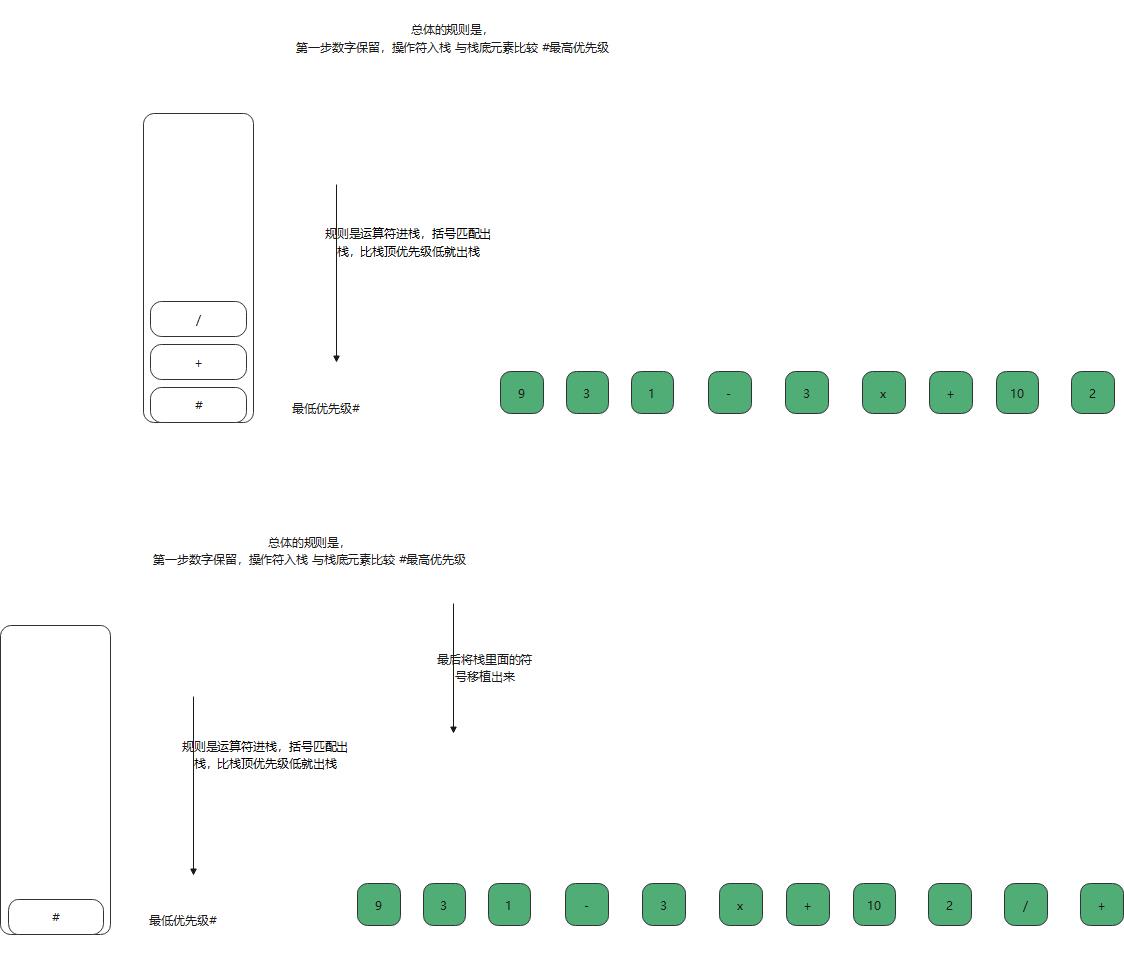
然后将数据进行计算

1。数字入栈
2.符号就取2个进行计算，再入栈

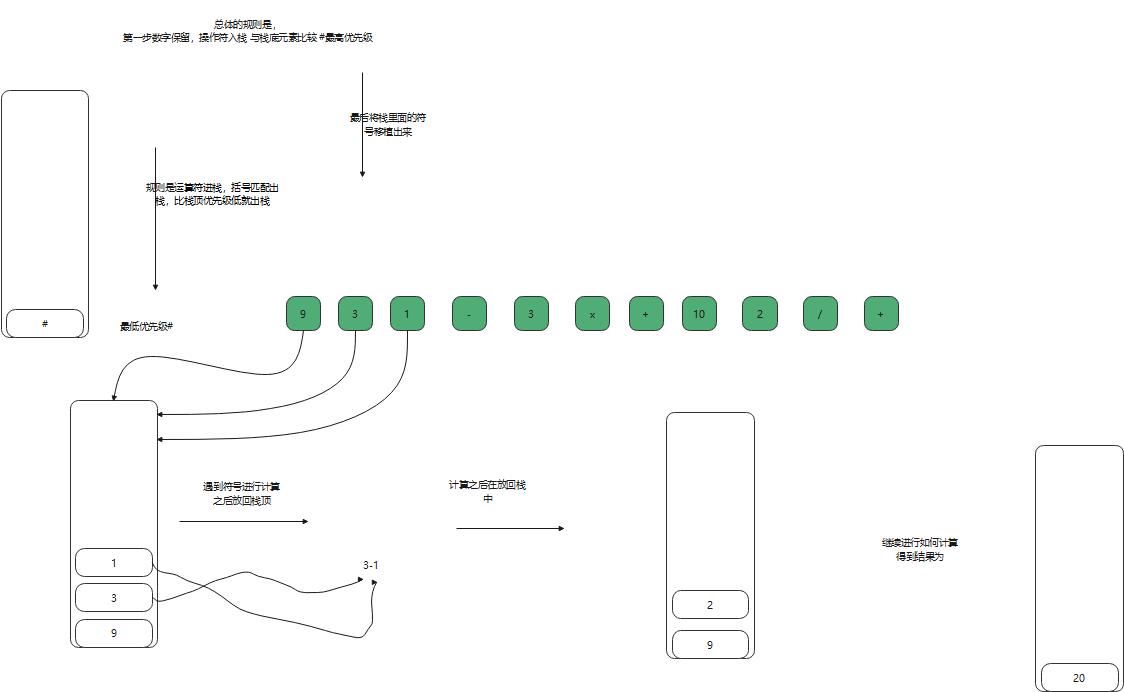
经过上面的步骤分析，使用运算符是非常多的步骤的，虽然很麻烦，但针对计算机来说这样还是很快的；在实际应用中还是应用的比较少，但是理解栈还是有学习的意义

递归 与栈

为什么说递归和栈的关系非常大，因为我们在调递归时，核心是方法栈进行调用

递归是什么

程序调用自身的编程技巧称为递归（recursion）。 递归做为一种算法在程序设计语言中广泛应用。一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，
递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说，递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

就像我们的分治法，都是将大问题变小问题，小问题的答案既是大问题的答案

递归执行特点

用下面的代码来理解  递归

    public void fun(int n){  //3
        System.out.println(n);
        if(n<0){
            return;
        }else{
            fun(n-1);
            System.out.println(n);
        }
    }

打印出来的 数是 3 2 1 0 -1 0 1 2 3 

调用自己 代码是怎么执行的

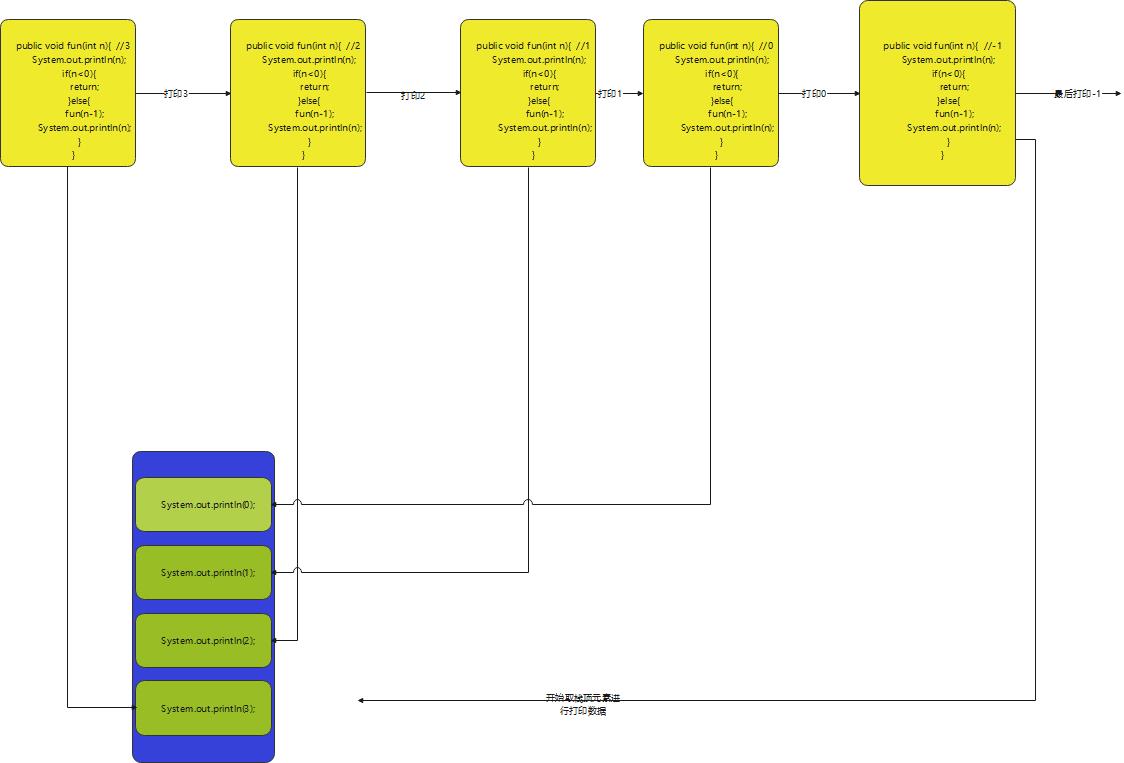
最后打印出来的数据，就打印的数据就是那样的

一般我们在实际的应用，是在 做一些实际问题的时候

递归应用

阶乘

例如 我们 1*2*3*4*5 。。。n!  比如 5！=5*4！ 因此 就是这样的

    public int fact(int n){
        if(n<=1){
            return 1;
        }else{
            return n*fact(n-1);
        }
    }

斐波拉契数列 

如 1   1  2  3  5  8   13  21  34  55  89  144......  数列的

    public int fibonacciSequence(int n){
        if(n==1 || n==2){
            return 1;
        }else{
            return fibonacciSequence(n-1)+fibonacciSequence(n-2);
        }
    }

就是往前面的数据  当前数据等于前面两位相加 ，这就是递归的算法，大问题进行转小问题

汉诺塔算法

这个算法的规定是大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

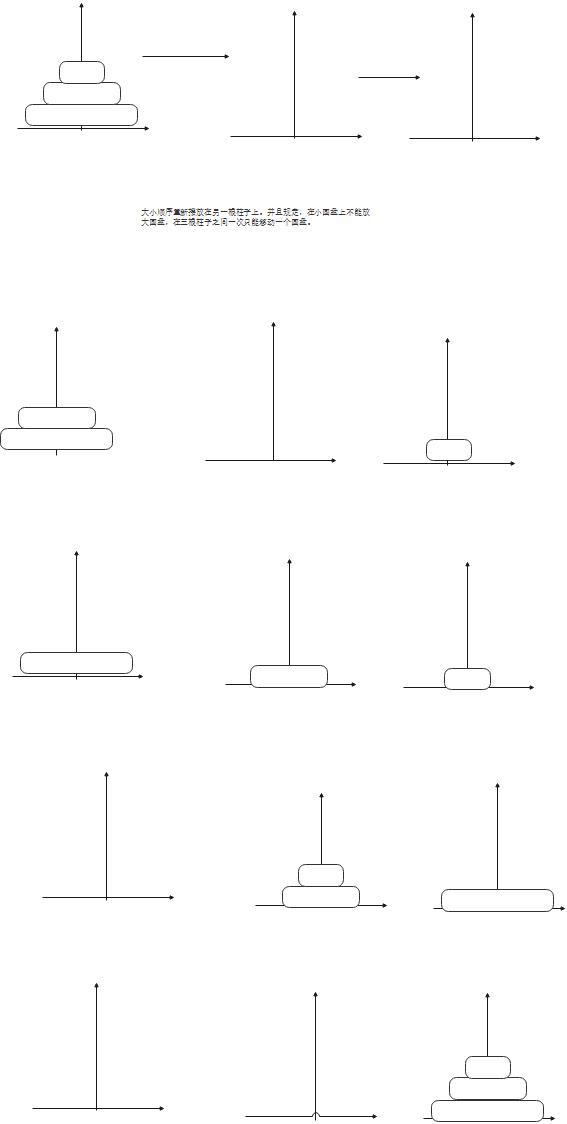
这画了个大概的思路，肯定我们在移动时，只能一个一个的移动 大的不能在小的上面，每次进行移动，代码的实现就是这样的，也就是中序遍历法

   /**
     * @param n      盘子的个数
     * @param start   开始的柱子
     * @param middle   中介柱子
     * @param end      结果柱子
     */
    public static void hanoi(int n,int start,int middle,int end){
        if(n<=1){
            System.out.println(start+"----->"+end);
        }else{
            hanoi(n-1,start,end,middle);
            System.out.println(start+"----->"+end);
            hanoi(n-1,middle,start,end);
        }
    }

可能大家还是没理解到为什么这段代码的意思  

• 以结束点为中点进行移动数据hanoi(n-1,start,end,middle);

 hanoi(n-1,start,end,middle);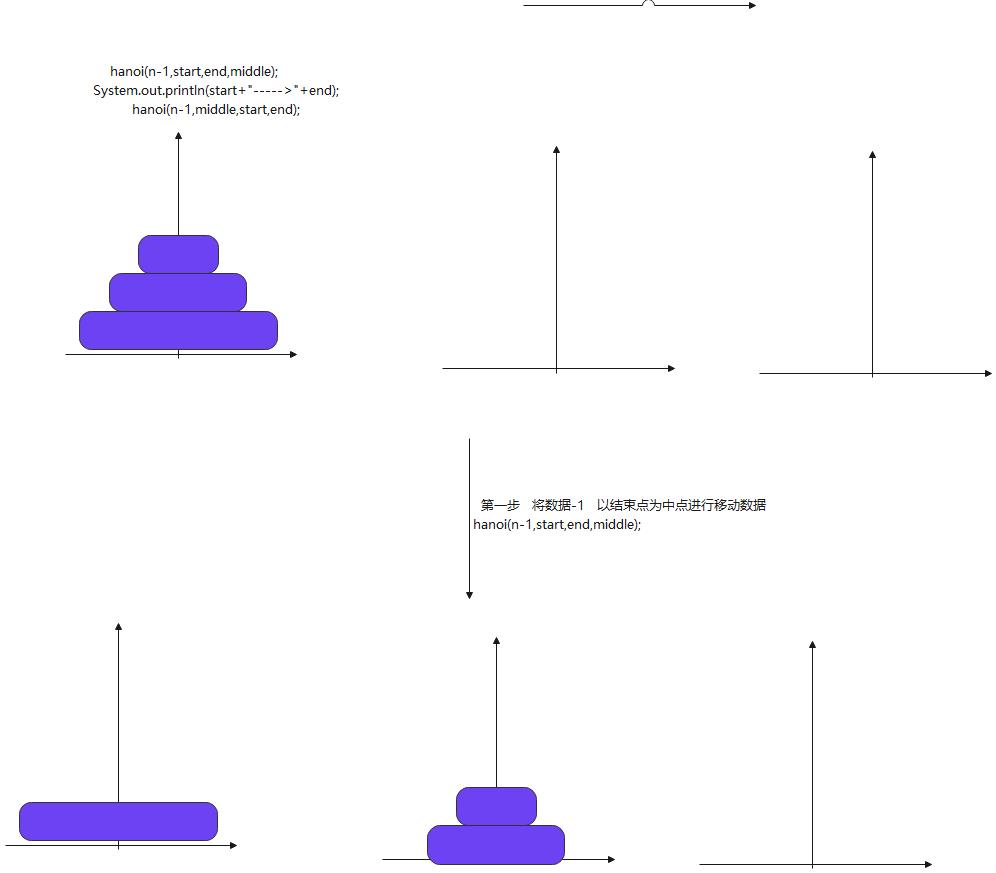

• 第二步将 开始节点移动到末尾节点

System.out.println(start+"----->"+end);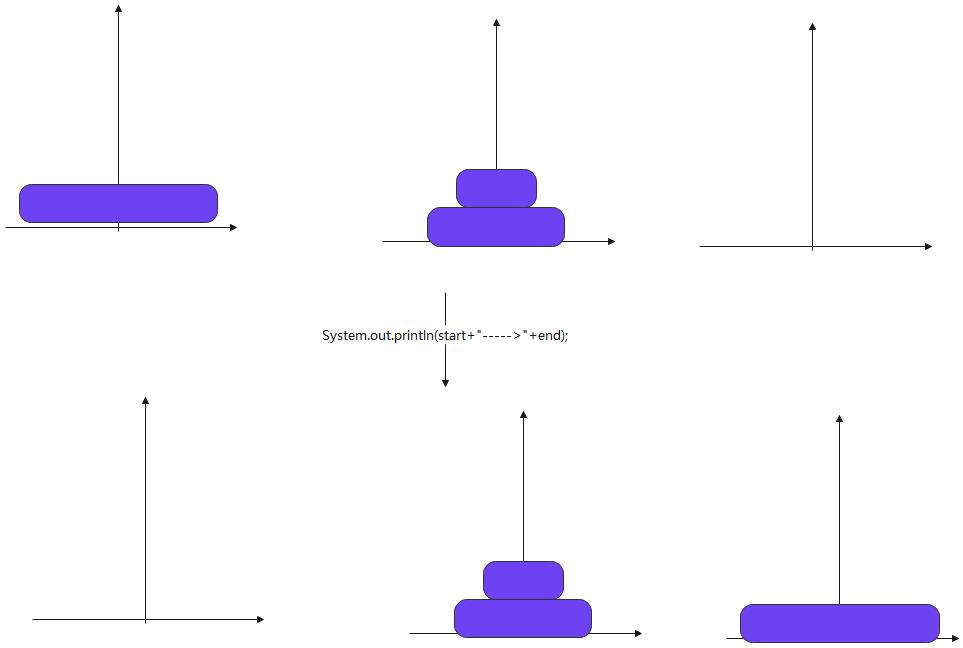

• 以开始为中心点，中部数据移动到结束点

 hanoi(n-1,middle,start,end);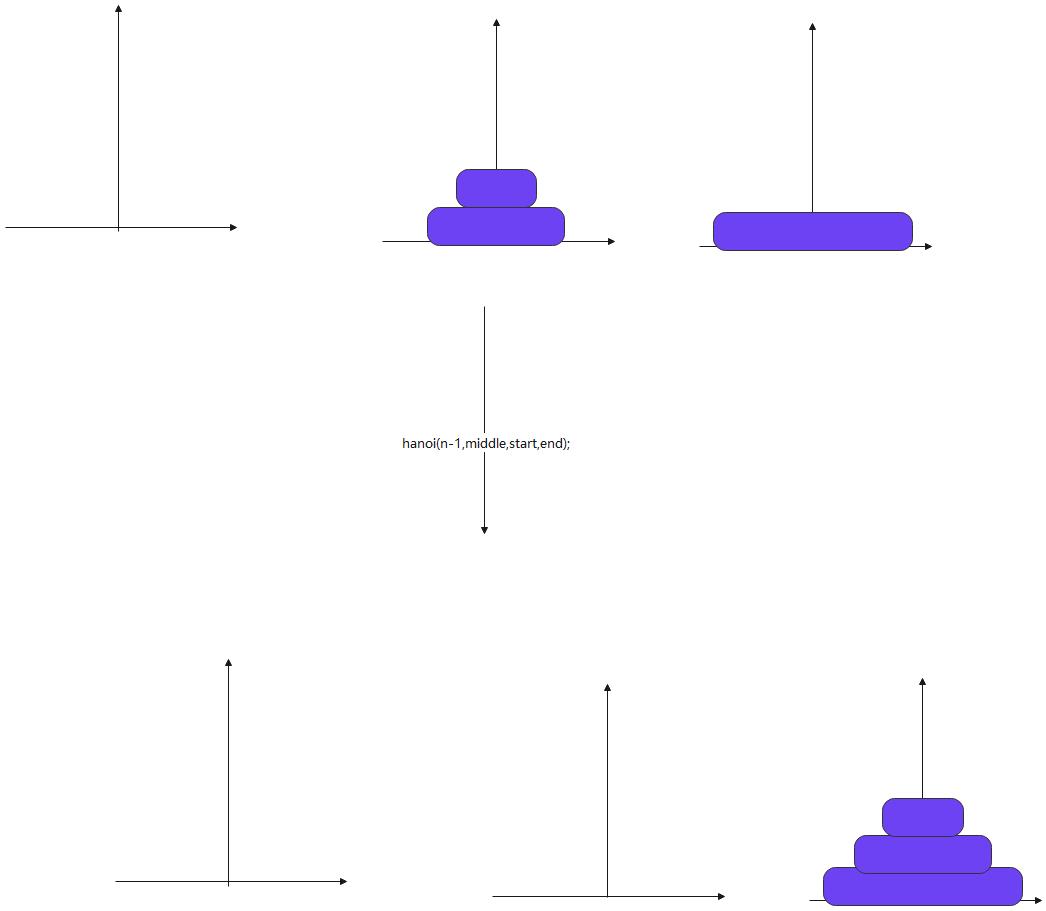

数据有多大，通过递归，可以从小问题进行解决

总结

本文介绍了栈是什么和栈的特性，从一些应用去介绍栈的应用，这个在我们应用中，一些可以大问题转小问题都可以使用递归和栈来解决，而且代码是很简洁