走进AI·机器学习の基本概念

Posted 2021-07-14 有理想、有本领、有担当的有志青年

机器学习の基本概念

• 一、机器学习の相关术语及其理解
• 二、机器学习の学习任务
• • 分类
  • 回归
  • 聚类
  • 特征降维与低维可视化
• 三、机器学习の学习范式
• • 监督式学习
  • 半监督式学习
  • 非监督式学习
  • 强化学习
• 四、假设&假设空间&版本空间
• 五、假设の选择原则
• • “奥克姆剃刀(Occam’s Razor)”准则
  • “多释原则”
• 六、机器学习の三要素
• • 模型
  • 策略
  • • 损失函数（代价函数）
    • 期望风险
    • 经验风险
    • 经验风险最小化策略
    • 结构风险最小化策略
  • 算法
  • • 常见算法
  • 方法=模型+策略+算法

---

机器学习 Machine Learning 是一门涉及统计学、系统辨识、逼近理论、神经网络、优化理论、计算机科学、脑科学等诸多领域的交叉学科，研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能，是人工智能技术的核心。基于数据的机器学习是现代智能技术中的重要方法之一，研究从观测数据（样本）出发 寻找规律，利用这些规律对未来数据或无法观测的数据 进行预测。
–人工智能标准化白皮书(2018版)

本文大纲基于河北师范大学软件学院张朝晖老师编写的PPT，以《统计学习方法》《机器学习》等书籍对内容加以补充，并辅以CSDN前辈大佬有关文章的启发，整理总结而成。最后，欢迎各位学弟学妹们报考河北师范大学软件学院！

一、机器学习の相关术语及其理解

• 样本sample：所研究对象的一个个体。相当于统计学中的实例（如河北师大学生对一票否决制的意见）

• 特征feature：研究对象的不同于其他对象的特点（如河北师大学生是否赞同一票否决制）

• 属性attribute：用数值表示的某些量化特征（如河北师大学生选择赞同则标记为1，不赞同标记为-1，无感的标记为0）

• 特征空间：分别以每个特征作为一个坐标轴，所有特征所在坐标轴张成一个用于描述不同样本的空间（如以河北师大学生大一到大四为纵坐标，以赞同，不赞同，无感为横坐标建立坐标系）每个具体样本就对应空间的一个点，在这个意义下，也称样本为样本点。特征的数目即为特征空间的维数。 模型都是定义在特征空间上的

• 输入空间：可能输入的所有元素的集合，其中输入变量用X表示

• 输出空间：可能输出的所有元素的集合，其中输出变量用Y表示

对特征空间，输入空间和输出空间的理解
把输入空间，输出空间分别看成一个房子，输入空间房子里有很多东西，输出空间里
有很多东西。输出空间里每一个东西，都能在输出空间房子里找到一个东西与它对应。
一般情况下，假设特征空间和输入空间没有区别。如果硬把他俩分开的话，特征空间
里每个变量都代表了不同的意义 x=(x(1),x(2),…,x(i),…,x(n)) x(i)表示x的第i
个特征向量

• 类别标签：为数据分类处理的依据（如河北师大学生依据年级分为大一到大四，大一到大四即为类别标签）

• 在机器学习和模式识别等领域中，一般需要将样本分成独立的三部分训练集（train set），验证集（validation set ) 和测试集（test set）。其中训练集用来估计模型，验证集用来确定网络结构或者控制模型复杂程度的参数，而测试集则检验最终选择最优的模型的性能如何。一个典型的划分是训练集占总样本的50%，而其它各占25%，三部分都是从样本中随机抽取。

二、机器学习の学习任务

分类

1. 基于已知类别标签的训练集出模型
2. 用最终的模型预测未知数据的分类结果
3. 预测结果为事先指定的两个或多个类别中的某一个，或预测结果来自数目有限的离散值之一

回归

1. 基于已知答案的训练集，估计自变量与因变量之间关系
2. 基于该关系对新的观测产生的输出进行预测
3. 预测输出为连续的实数值

聚类

1. 划分给定的数据集，得到若干“簇”；
2. “簇内”样本之间较“簇间”样本之间应更为相似。
3. 通过聚类得到的可能各簇对应一些潜在的概念结构
4. 聚类是自动为给定的样本赋予标记的过程。

特征降维与低维可视化

1. 将初始的数据高维表示转化为关于样本的低维表示，来简化输入
2. 对降维后的数据进行可视化表示

三、机器学习の学习范式

监督式学习

• 目的在于精确预测
• 适用于面向分类模型，回归模型的分析
• 预测性能
• 基于已知标签的数据集学习预测模型，基于该模型对未知样本的输出做出预测。

半监督式学习

• 基于少量有标签样本(标注成本高)、大量无标签样本(获取容易)学习输入到输出的预测模型。
• 充分利用无标签样本的信息，辅助有标签的样本，进行监督学习
• 以较低成本获得较好的学习效果。

非监督式学习

• 目的在于发现关于数据的紧致描述、知识发现
• “描述性能”
• 算法基于无标签样本集进行模型学习，基于学得的模型对所
  有未知样本做出预测。

强化学习

• 借助智能体与环境的连续互动，学习最优行为策略
• 以试错方式，使智能体学得当前环境状态到行为的映射，使得智能体能结合环境状态，选择能够获得环境最大奖赏的行为
• 结合给定的奖惩机制，算法学习如何与环境交互，以便智能体对环境采取更好的动作行为。
• 典型应用：下棋、无人驾驶

四、假设&假设空间&版本空间

• 每一个具体的模型就是一个 “假设(hypothesis)”
• 所有模型的集合即 假设空间
• 模型的学习过程就是一个在所有假设构成的假设空间进行搜索的过程，搜索的目标就是找到与训练集“匹配(fit)”的假设。
• 基于有限规模的训练样本集进行假设的匹配搜索，会存在多个假设与训练集一致的情况，称这些假设组成的集合为 “版本空间”

五、假设の选择原则

“奥克姆剃刀(Occam’s Razor)”准则

• 如无必要，勿增实体
• 若多个假设与经验观测一致，则选择最简单的那个

“多释原则”

• 保留与经验观察一致的所有假设 (与集成学习的思想一致)

六、机器学习の三要素

模型

• 首先要确定需要学习什么样的模型

策略

• 机器学习的目标在于从假设空间中选取最优模型
• 策略就是确定基于什么样的准则 ，学习或选择最优模型。
• 实质：面向具体模型的学习，确定准则函数（也称损失函数、代价函数、目标函数）

损失函数（代价函数）

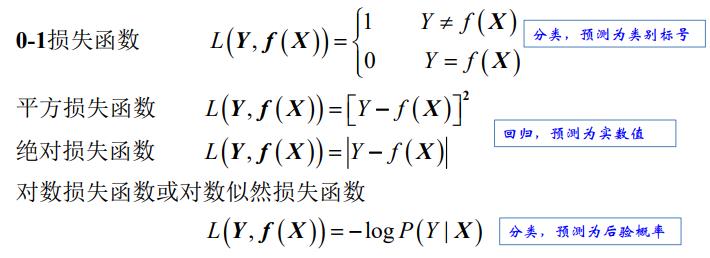
• 损失函数值越小越好

期望风险

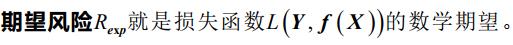
• 机器学习的目标在于选择期望风险最小的模型
• 但因联合分布P （X,Y）未知，难以计算

经验风险

• 对所有训练样本都求一次损失函数，再累加求平均。即模型f(x)对训练样本中所有样本的预测能力。
• 所谓经验风险最小化即对训练集中的所有样本点损失函数的平均最小化。经验风险越小说明模型f(x)对训练集的拟合程度越好。
• 实际问题中，训练样本数目N非常有限，需对经验风险矫正

经验风险最小化策略

• 在假设空间、损失函数形式、以及训练样本集确定的前提下
• 假设空间中，使经验风险最小的模型，就是最优模型。
• 当容量足够大时效果好
• 当容量小时，容易产生过拟合

结构风险最小化策略

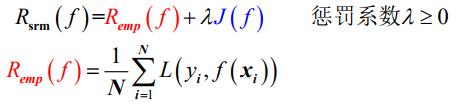
• J(f) 是模型的复杂度，模型f越复杂，J(f)值就越大
• λ 是正则项的系数，λ≥0 ，用以权衡经验风险和模型复杂度。
• 值越小，模型关于训练集的学习能力越好

算法

• "算法"是指采用何种算法，求解最优化问题

常见算法

• 决策树（Decision Trees）
• 朴素贝叶斯分类(Naive Bayesian classification)
• 最小二乘法（Ordinary Least Squares Regression）
• 逻辑回归(Logistic Regression)
• 支持向量机（Support Vector Machine，SVM）
• 集成方法（Ensemble methods）
• 聚类算法（Clustering Algorithms）
• 主成分分析（Principal Component Analysis，PCA）
• 奇异值分解（Singular Value Decomposition，SVD）
• 独立成分分析（Independent Component Analysis，ICA）

方法=模型+策略+算法