Java算法——排序
Posted 364.99°
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Java算法——排序相关的知识,希望对你有一定的参考价值。
目录
1.冒泡排序
1.1.排序原理
- 相邻元素(arr[j]与arr[j+1]) 比较,前一个元素比后一个元素大,则交换两元素的位置
- 对每一对相邻元素做上述操作,从第一对元素到最后一对元素,最终实现最大的元素排在最后一位
- 重复上述操作,直到排序完成
1.2.代码实现
public class Bubble {
public static void sort(int []arr){
for (int i = arr.length-1;i > 0;i--){//每次
for (int j = 0;j < i;j++){
int temp;
//比较,交换顺序
if (arr[j] > arr[j+1]){
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
}
import java.util.Arrays;
public class TestSort {
public static void main(String[] args) {
int[] a = {4,5,9,7,1,3,5};
System.out.println("排序前数组:" + Arrays.toString(a));
Bubble.sort(a);
System.out.println("排序后数组:" + Arrays.toString(a));
}
}

1.3.复杂度分析
双层for循环,内循环完成排序,故主要分析内循环
最坏情况: 数组完全逆序
- 元素比较次数:(N-1)+(N-2)+…+2+1 = N^2/2 - N/2
- 元素交换次数:(N-1)+(N-2)+…+2+1 = N^2/2 - N/2
- 总执行次数:N^2 - N
O(N^2)
2.选择排序
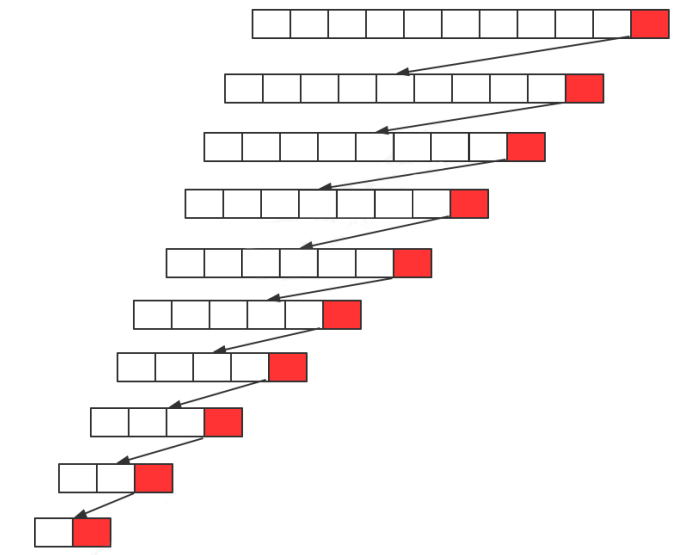
2.1.排序原理
- 找到最小值元素所在位置: 每一次遍历,都设定首位元素为最小值,与其他位的元素进行比较,如果其他位的元素更小,则将其他位设定为最小值,最后可以找到最小值所在的位置
- 交换位置: 交换首位元素与最小值元素的位置
2.2.代码实现
public class Selection {
public static void sort(int[] arr){
for (int i = 0;i < arr.length-2;i++){
//设置arr[i]为最小值所在位置
int minIdex = i;
for (int j = i+1;j < arr.length;j++){
if (arr[minIdex] > arr[j]){
//交换最小值下标
minIdex = j;
}
}
//交换位置
int temp = arr[i];
arr[i] = arr[minIdex];
arr[minIdex] = temp;
}
}
}
2.3.复杂度分析
双层for循环,外层实现数据交换,内层实现数据比较,分别统计交换次数与比较次数
最坏情况:
- 元素比较次数:(N-1)+(N-2)+…+2+1 = N^2/2 - N/2
- 元素交换次数:N-1
- 时间复杂度:N^2/2 - N/2 + (N-1) = N^2/2 + N/2 - 1;
O(N^2)
3.插入排序
3.1.排序原理
- 分组: 把所有数据分为两组,已经排序和未经排序(默认第一个元素为已排序元素)
- 选择插入元素: 将未排序组中的第一个元素,插入已排序组中
- 倒序比较插入: 倒序遍历已排序组的元素,依次和待插入的元素进行比较,直到找到一个元素<=待插入元素,就把待插入元素放置在此位置,其他元素向后移动一位
3.2.代码实现
public class Insertion {
public static void sort(int[] a){
for (int i=1;i < a.length;i++){
//当前未排序首位元素为a[i],与之前的元素进行比较,直到找到小于等于a[i]的元素,跳出循环
for (int j=i;j > 0;j--){
if (a[j] < a[j-1]){
int temp = a[j-1];
a[j-1] = a[j];
a[j] = temp;
}else{
//找到最终插入位置,跳出循环
break;
}
}
}
}
}
3.3.复杂度分析
双层for循环,内层完成排序,主要分析内层循环体执行次数
最坏情况
- 比较次数:(N-1)+(N-2)+…+2+1 = N^2/2 - N/2
- 交换次数:(N-1)+(N-2)+…+2+1 = N^2/2 - N/2
- 总执行次数:N^2 - N
O(N^2)
上述三种排序时间复杂度都是O(N^2),不适合大规模输入
以下为一些较为高级的算法,争取降低算法时间的最高次幂
4.希尔排序
又名“缩小增量排序”,插入排序的升级版
4.1.排序原理
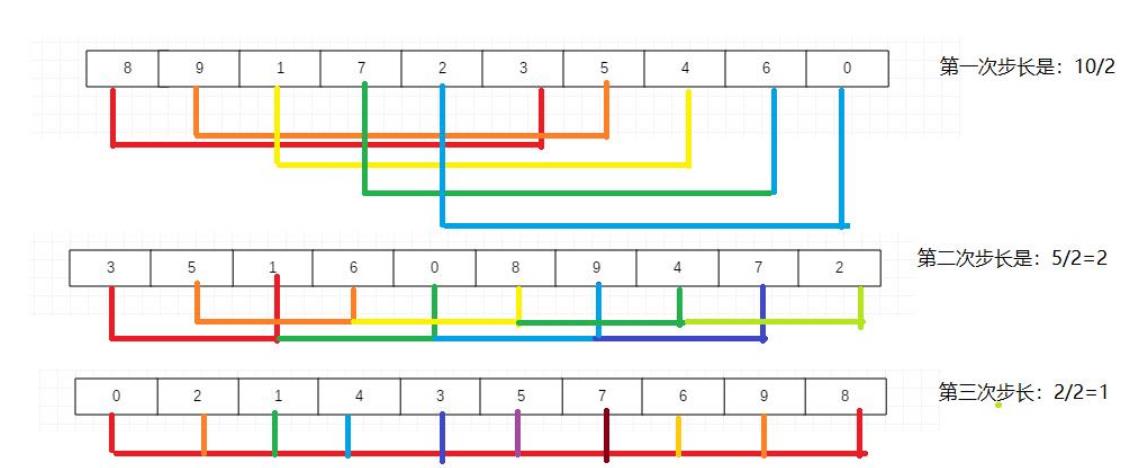
- 选择定一个增长量h=5,将增长量作为元素分组的依据,对元素进行分组
- 对分好的每一组数据完成插入排序
- 减少增长量,重复第二步操作,直到增长量h减小为1,完成排序
增长量h的取值规则:
最大值:
int h = 1
while (h < n/2){//n排序数组长度
h = 2h + 1;
}
减小:h=h/2
4.2.代码实现
public class Shell {
public static void sort(int[] a){
//数组长度为n
int n = a.length;
//确定增长量h的最大值
int h = 1;
while (h < n/2){
h = 2*h + 1;
}
//开始排序
while (h >= 1){
for (int i=0;i < n;i++){
//a[j]为待插入元素,依次和a[j-h],a[j-2h],a[j-3h]...比较,如果a[j]小,则交换位置,否则a[j]完成插入,跳出循环
for (int j=i;j >= h;j -= h){
if (a[j] < a[j-h]){
int temp = a[j];
a[j] = a[j-h];
a[j-h] = temp;
}else {
break;//跳出循环
}
}
}
h /= 2;//h缩减
}
}
}
4.3.复杂度分析
因为增长量h没有固定规则,故可以使用事后分析法及逆行分析
经过测试,在处理大量数据时,希尔排序的性能确实优于插入排序
5.归并排序
归并排序是建立在归并操作上的一种有效的排序方法,该算法是采用分治法的一个非常典型的例子。
将已有序的子序列合并,得到完全有序的序列(先使子序列有序,再使子序列间有序),将两个子序列表合并成一个有序表,称为二路归并
5.1.递归
在定义方法时,在方法内部调用方法本身,为递归
将一个大型复杂的问题,层层转换为一个与原问题相似的,规模较小的问题来求解,大大地减少了程序的代码量
注意: 在递归中不能无限制地调用自己,必须要有边界条件,能够让递归结束。每一次地柜都会在栈内开辟新的空间,重新执行方法,递归的层级太深,很容易造成栈内存溢出。
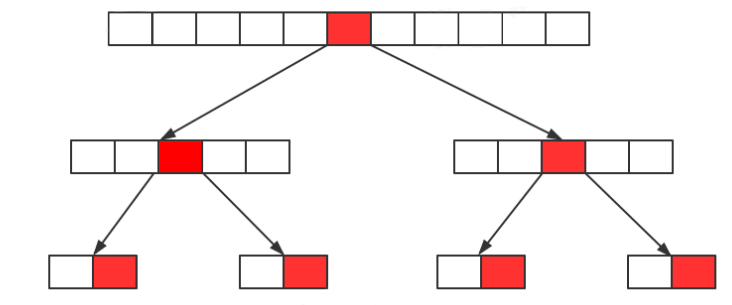
如:实现二叉树的数据填充方法
通过递归调用add方法,实现左子节点与右子节点的数据插入
public class Node {
//左子节点
public Node leftNode;
//右子节点
public Node rightNode;
//值
public Object value;
//插入数据的方法
public void add(Object v){
//当前节点没有值,就将v赋值给value
if (null == value)
value = v;
else {
if ((Integer) v - ((Integer) value) <= 0){
if (null == leftNode)
leftNode = new Node();
leftNode.add(v); //使用递归
}
else {
if (null == rightNode)
rightNode = new Node();
rightNode.add(v);
}
}
}
5.2.归并排序原理
- 尽可能地将一组数据拆分为两个元素数相等的子组,并对每一个子组继续拆分,直到拆分后的每个子组的元素个数都是1为止
- 将相邻的两个子组进行合并成一个有序的大组
- 不断地重复步骤2,直到最终只有一个组为止
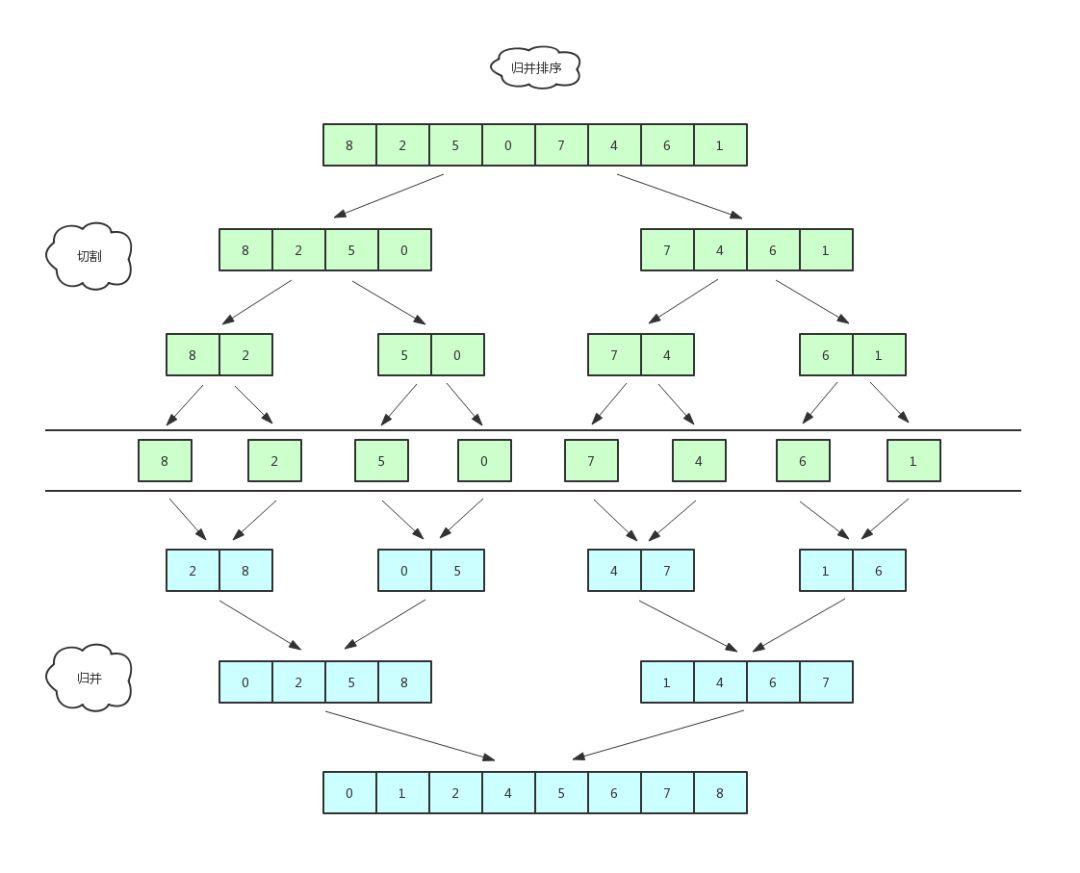
5.3.代码实现
package Test;
public class Merge {
//创建辅助数组
private static int[] assist;
/*
排序数组a的元素
*/
public static void sort(int[] a){
assist = new int[a.length];
//创建两个原数组的指针,start:最小索引指针,end:最大索引指针
int start = 0;
int end = a.length - 1;
//对数组a进行拆分,排序,合并
sort(a,start,end);
}
/*
先拆分,后排序合并数组a
*/
private static void sort(int[] a,int start,int end){
//判断,当,end <= start时,说明拆分到最小单位,结束方法
if (end <= start){
return;
}
//定义一个中间指针,实现从中拆分
int middle = start + (end - start)/2;
//递归调用sort进行拆分
sort(a,start,middle);
sort(a,middle+1,end);
//调用merge函数进行归并
merge(a,start,middle,end);
}
/*
排序,合并数组(归并)
*/
private static void merge(int[] a,int start,int middle,int end){
//定义辅助函数插入数据的指针
int i = start;
//创建两个子数组的初始位置指针
int pointer1 = start;
int pointer2 = middle + 1;
//当两个子数组指针都未越界时,两子数组进行比较排序插入辅助数组
while (pointer1 <= middle && pointer2 <= end){
if (a[pointer1] < a[pointer2]){
assist[i++] = a[pointer1++];
}else {
assist[i++] = a[pointer2++];
}
}
//当有一个子数组的指针到了边界,就只进行剩余的数组的数据插入,以下两循环只进行一个
while (pointer1 <= middle){
assist[i++] = a[pointer1++];
}
while (pointer2 <= end){
assist[i++] = a[pointer2++];
}
//当assist数组中所有数据完成排序,就拷贝到原数组
for (int j=start;j <= end;j++){
a[j] = assist[j];
}
}
}
5.4.复杂度分析
归并排序是分治思想最典型的例子,先将数组进行拆分为(尽量)等长的两部分,分别通过递归调用将它们单独排序,最后将有序的数组归并为最终的排序结果。
该递归的出口在于:如果一个数组不能再被分成两个数组,就执行merge进行归并,在归并的时候比较元素的大小进行排序
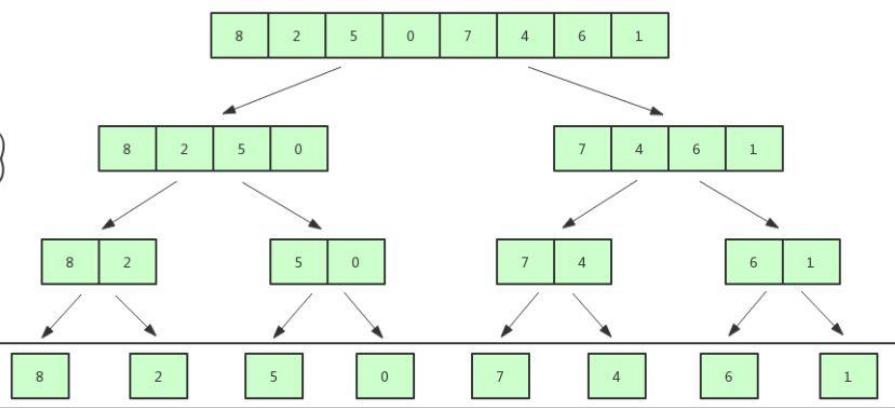
复杂度分析:
输入元素个数为n,使用归并排序的拆分次数:log2(n),所以会有log2(n)层树,,故自顶向下第k层有2^k个子数组,每个数组长度 2^(log2(n)-k) ,归并最多需要 2^(log2(n)-k) 次比较,因此每层的比较次数为
2^k*2^(log2(n)-k) = 2^log2(n),n层就是log2(n)*2^(log2(n)) = log2(n)*n
O(nlogn)
6.快速排序
冒泡排序法的升级版,基本思想:通过一次排序,将要排序的数据分成独立的两个部分,其中一部分的所有数据都比另一部分的所有数据要小,然后重复此步骤对两个部分数据分别进行排序。
6.1.切分原理
- 找一个基准值,用两个指针分别指向数组的头部和尾部
- 先从尾部向头部开始搜索一个比基准值小的元素,搜索到即停止,并记录指针的位置
- 再从头部向尾部开始搜索一个比基准值大的元素,搜索到即停止,并记录指针的位置
- 交换当前左边指针位置和右边指针位置的元素
- 重复2,3,4步骤,直到左边指针的值大于右边指针的值停止
6.2.排序原理
- 设定一个分界值,通过此分界值将数组分为左右两个部分
- 将>=分界值的数据放到数组右侧,<=分界值的数据放到数组左侧,
- 对左右两边的数据进行独立排序,两边数组的数据又可以取分界值,分别划分为两个子数组左边较小值,右边较大值
- 重复上述步骤,通过递归实现。通过递归先将左侧数据排序,再排序右侧数据,当两侧数据都排序好,整个数组也就排序好了
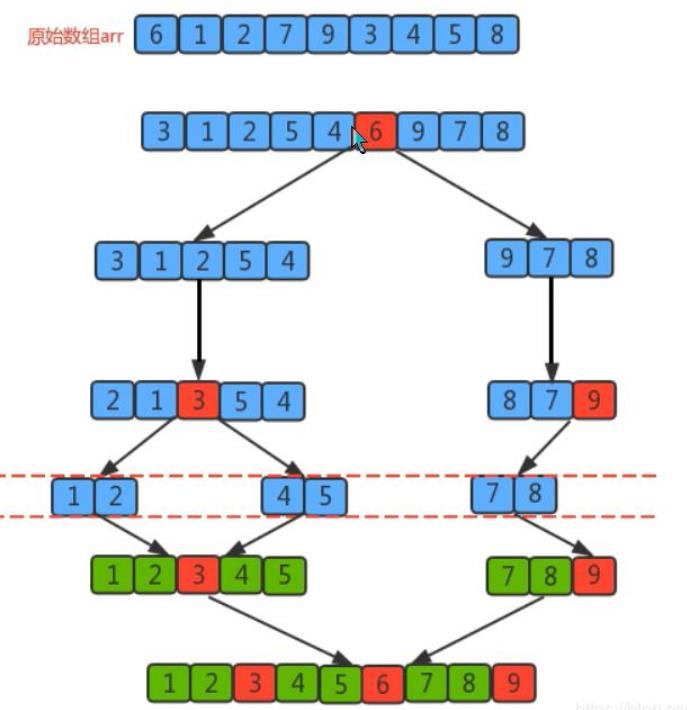
6.3.代码实现
public class Quick {
/*
排序总方法
*/
public static void sort(int[] a){
int start = 0;
int end = a.length - 1;
//排序素组所有元素
sort(a,start,end);
}
/*
切分排序
*/
private static void sort(int[] a,int start,int end){
//安全性检测
if (end <= start){
return;
}
//对数组a的start到end的元素进行切分
int partition = partition(a,start,end);
//对左子祖进行排序
sort(a,start,partition - 1);
//对右子组进行排序
sort(a,partition + 1,end);
}
/*
切分
*/
public static int partition(int[] a,int start,int end){
//基准值(切分中间值)
int mid = a[start];
//左指针
int left = start;
//右指针
int right = end + 1;
//进行切分
while (true){
//从右到左扫描,找到比mid小的数值,则停止
while (a[--right] > mid){
//当整个数组没有比mid小的数值时,跳出循环
if (right == left){
break;
}
}
//从左到右扫描,找到比mid大的数值,则停止
while (a[++left] < mid){
//当整个数组没有比mid大的数值时,跳出循环
if (left == end){
break;
}
}
//交换上述两个步骤扫描到的数值的位置
if (left >= right){
//扫描完所有数据
break;
}else {
//交换数组left与right处的值
exch(a,left,right);
}
//right就是切分界限
}
//交换最后right索引处和基准值所在的索引处的值
exch(a,start,right);
return right;
}
private static void exch(int[] a,int i,int j){
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
6.4.复杂度分析
快速排序的一次切分从两头开始交替搜索,直到left和right重合,因此,一次切分算法的时间复杂度为O(n),但整个快速排序的时间复杂度和切分次数有关
最优情况:
每一次切分选择的基准数字刚好将当前序列等分
共切分logn次
时间复杂度:O(nlogn)
最坏情况:
每一次切分选择的基准数字是当前序列中最大数或者最小数,这使得每次切分都会有一个子组,那么总
共就得切分n次
时间复杂度为O(n^2)
7.排序的稳定性
数组arr中有若干元素,其中A元素和B元素相等,并且A元素在B元素前面,如果使用某种排序算法排序后,能够保
证A元素依然在B元素的前面,可以说这个该算法是稳定的
7.1.稳定性的意义
如果一组数据只需要一次排序,则稳定性一般是没有意义的,如果一组数据需要多次排序,稳定性是有意义的。例
如要排序的内容是一组商品对象,第一次排序按照价格由低到高排序,第二次排序按照销量由高到低排序,如果第
二次排序使用稳定性算法,就可以使得相同销量的对象依旧保持着价格高低的顺序展现,只有销量不同的对象才需
要重新排序。这样既可以保持第一次排序的原有意义,而且可以减少系统开销
7.2.常见排序算法的稳定性
冒泡排序
只有当arr[i]>arr[i+1]的时候,才会交换元素的位置,而相等的时候并不交换位置,所以冒泡排序是一种稳定的排序
算法
选择排序
选择排序是给每个位置选择当前元素最小的,例如有数据{5(1),8 ,5(2), 2, 9 },第一遍选择到的最小元素为2,
所以5(1)会和2进行交换位置,此时5(1)到了5(2)后面,破坏了稳定性,所以选择排序是一种不稳定的排序算法
插入排序
比较是从有序序列的末尾开始,也就是想要插入的元素和已经有序的最大者开始比起,如果比它大则直接插入在其
后面,否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的,那么把要插入的元素放在相等
元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序
是稳定的
希尔排序
希尔排序是按照不同步长对元素进行插入排序 ,虽然一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以希尔排序是不稳定的
归并排序
归并排序在归并的过程中,只有arr[i]<arr[i+1]的时候才会交换位置,如果两个元素相等则不会交换位置,所以它
并不会破坏稳定性,归并排序是稳定的
快速排序
快速排序需要一个基准值,在基准值的右侧找一个比基准值小的元素,在基准值的左侧找一个比基准值大的元素,然后交换这两个元素,此时会破坏稳定性,所以快速排序是一种不稳定的算法
以上是关于Java算法——排序的主要内容,如果未能解决你的问题,请参考以下文章