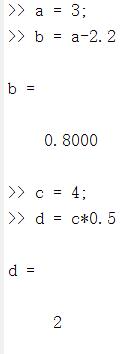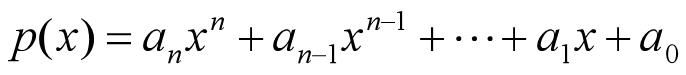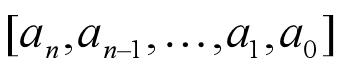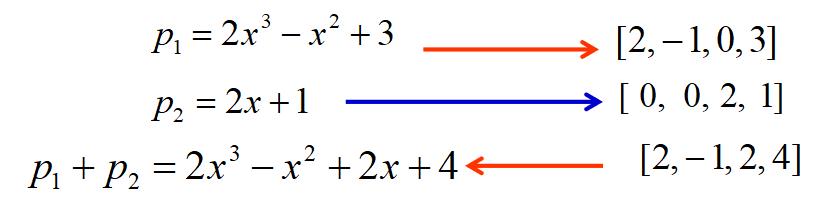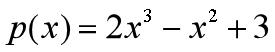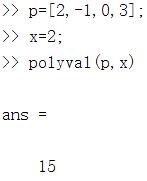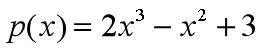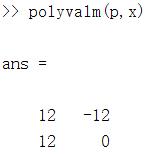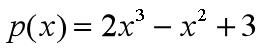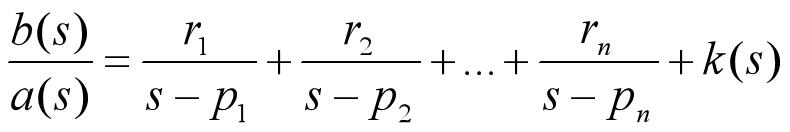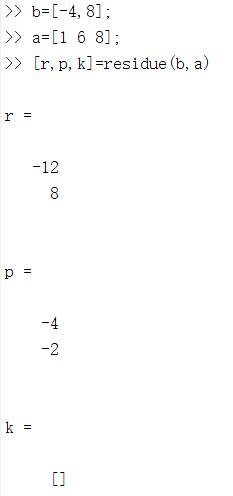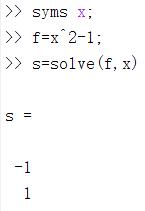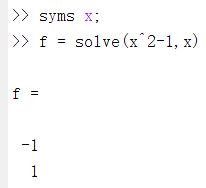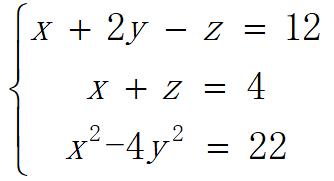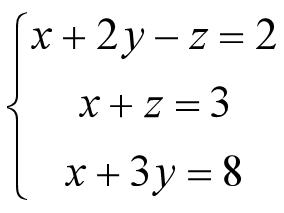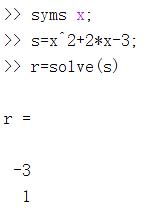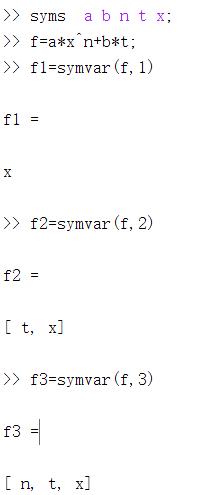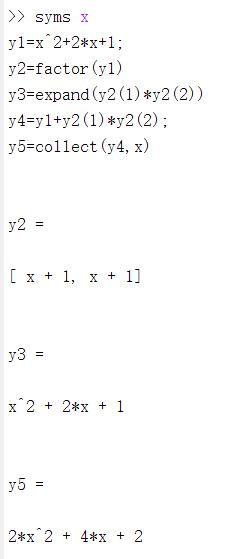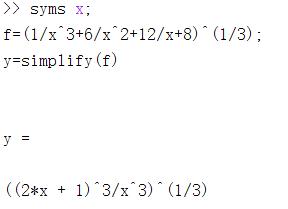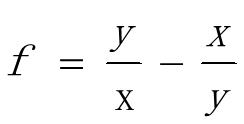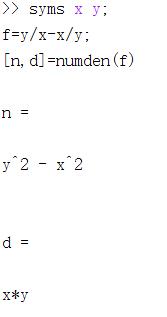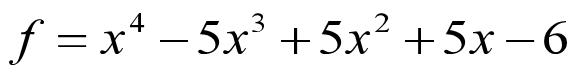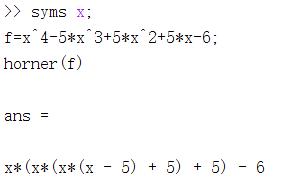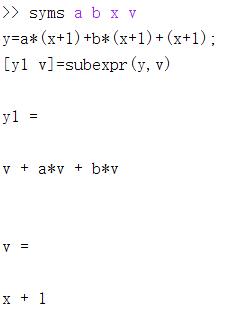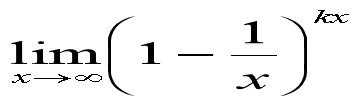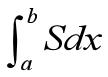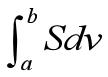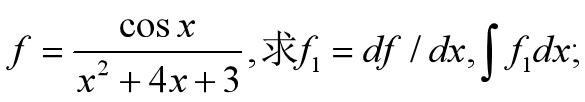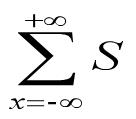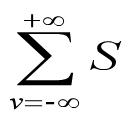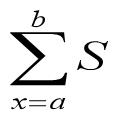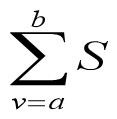MATLAB基础2.0

Posted 2021-07-12 364.99°

数据类型、矩阵运算、多项式运算、字符变量与符号矩阵、复变函数

---

目录

• 1.常用数据类型
• • 1.1.numeric（数值型）
  • 1.2.显示精度
  • 1.3.char（字符型）
  • 1.4.数据类型之间的转换
  • 1.5.logic（逻辑型）
  • 1.6.cell（单元型）
  • 1.7.struet（结构型）
  • 1.8.函数句柄
• 2.数值矩阵运算
• • 2.1.矩阵的建立
  • 2.2.数值矩阵运算
  • • 2.2.1.建立向量
    • 2.2.2.矩阵元素的使用
    • 2.2.3.矩阵拆分
    • 2.2.4.矩阵元素的删除
    • 2.2.5.矩阵变换函数
    • 2.2.6.常见生成函数
    • 2.2.7.矩阵算法
• 3.多项式及其运算
• • 3.1.加减运算
  • 3.2.乘除运算
  • 3.3.求导运算
  • 3.4.多项式求值
  • 3.5.多项式求根
  • 3.6.部分分式展开
  • 3.7.求解方程
• 4.字符串变量与符号矩阵
• • 4.1.数值运算与符号运算
  • 4.2.创建符号变量和表达式
  • 4.3.创建符号矩阵
  • 4.4.默认符号变量的查询
  • 4.5.符号表达式的化简
  • 4.6.符号表达式的替换
  • 4.7.符号极限
  • 4.8.符号微分
  • 4.9.符号积分
  • 4.10.符号求和
• 5.有关复变函数的函数

1.常用数据类型

1.1.numeric（数值型）

1.整数

带符号整数与无符号整数

数值类型	取值范围	转换函数
Signed 8-bit integer	-2^7 to 2^7-1	int 8
Signed 16-bit integer	-2^15 to 2^15-1	int 16
Signed 32-bit integer	-2^31 to 2^31-1	int 32
Unsigned 8-bit integer	0 to 2^8-1	uint 8
Unsigned 16-bit integer	0 to 2^16	uint 16
Unsigned 32-bit integer	0 to 2^32	uint 32
Unsigned 64-bit integer	0 to 2^64	uint 64

2.浮点数

双精度（默认双精度）

双精度浮点数参与运算时，返回值的类型依赖于参与运算的其他数据类型。
参与运算的其他数据为逻辑型，字符型时，返回结果为双精度浮点型

参与运算的其他数据为整数型时，返回结果为相应的整数类型

参与运算的其他数据为单精度浮点数型时，返回结果为相应的单精度浮点数型类型

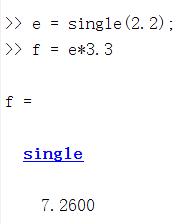
单精度（single）

单精度浮点类型不能与整数类型进行算术运算

3.复数

1.声明

%直接输入
z0 = 1 + 2i;
z1 = 1 + 2j;
%complex声明
z2 = complex(1,2);

2.函数

函数	说明
isreal	判断数组是否为实数数组 1(true) 0(false)
real	返回实部
imag	返回虚部
abs	返回复数幅值
angle	返回相位角（弧度制）
polar	极坐标图

1.2.显示精度

1.默认状态

1.整数以整型显示
2.实数，保留小数点后4位显示

2.函数

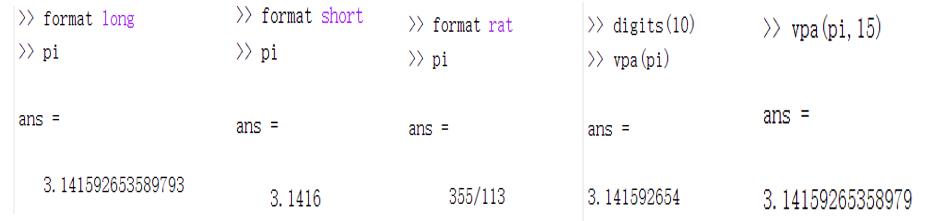
format:不改变原始数据，只影响其在命令窗口的显示
digits，vpa:控制显示精度

1.3.char（字符型）

1.声明

%使用单引号 ''为字符声明
str0 = 'character';
class(str0)              %返回数值类型

%使用双引号""为字符串声明
str1 = "string"
class(str1)

%使用syms声明
syms x

2.计算

字符类型参与计算时，数值大小为对应ascll码的数值大小
abs：查看字符对应的ascll码值

3.字符串连接

垂直连接：
    strvcat(str1,str2)：自动为较短的字符串补足空格，保持两个字符串等长度
    [str1;str2]：需要手动补足空格

4.函数

函数	说明	函数	说明
strcmp	比较字符串	strrep	替换字符串
strcmpi	忽略大小写比较字符串	upper	转换为大写
strncmp	比较字符串的前n个字符	lower	转换为小写
findstr	在长字符串中查找短字符串	strtok	返回字符串中的第一个分隔符（空格、回车、Tab）前的部分
strjust	对齐字符串数组（左、中、右）	blanks	产生空字符串
strmatch	查找匹配字符串	deblank	删除字符串末尾的空格

1.4.数据类型之间的转换

函数	说明	函数	说明
int2str	整数转字符串	dec2bin	十进制转二进制
mat2str	矩阵转字符串	dec2hex	十进制转十六进制
num2str	数字转字符串	hex2dec	十六进制转十进制
str2num	字符串转数字	hex2num	十六进制转数字
bin2dec	二进制转十进制	num2hex	数字转十六进制

字符串转换为数值代码：abs、double
按照ascll码转换：abs、double、char
直接转换：num2str、mat2str、str2num

1.5.logic（逻辑型）

1：表示逻辑真（true）
0：表示逻辑假（false）

true(n)/true(m,n)：创建元素全为1（真）的矩阵
false(n)/false(m,n)：创建元素全为0（假）的矩阵
logical：将矩阵转换成逻辑值，非零元素转换成逻辑真，零元素转换成逻辑假

1.6.cell（单元型）

元胞数组（cell）：可以存放任意类型、任意大小的数组，同一元胞数组中各元胞的内容可以不同

1.声明

1.赋值语句直接定义
today = cell{'初八',5 19,'Thursday'}
2.cell赋值
today = cell(1,4)预分配内存
today = {'初八',5 19,'Thursday'}赋值
3.访问
()访问cell单元
{}访问cell内存

3.cell的连接转置

c = [a,b] %水平连接a,b
c = [a;b] %垂直连接
c = a’ %a的转置

4.cell元素的删除[ ]

a(:) = [ ] %删除所有单元
a(1) = [ ] %删除第一个单元
a{1} = [ ] %将第一个单元编程空值

5.函数

函数	说明
cell	生成元胞数组变量
celldisp	显示元胞数组变量的内容
cellplot	图形显示元胞数组变量的内容
num2cell	将数值数组转换成元胞数组
iscell	判断是否为元胞数组变量

1.7.struet（结构型）

包含已命名“数据容器”或域的数组，结构类型数组中的域可以包含任意类型的数据；是用指针的方式传递数据

1.声明

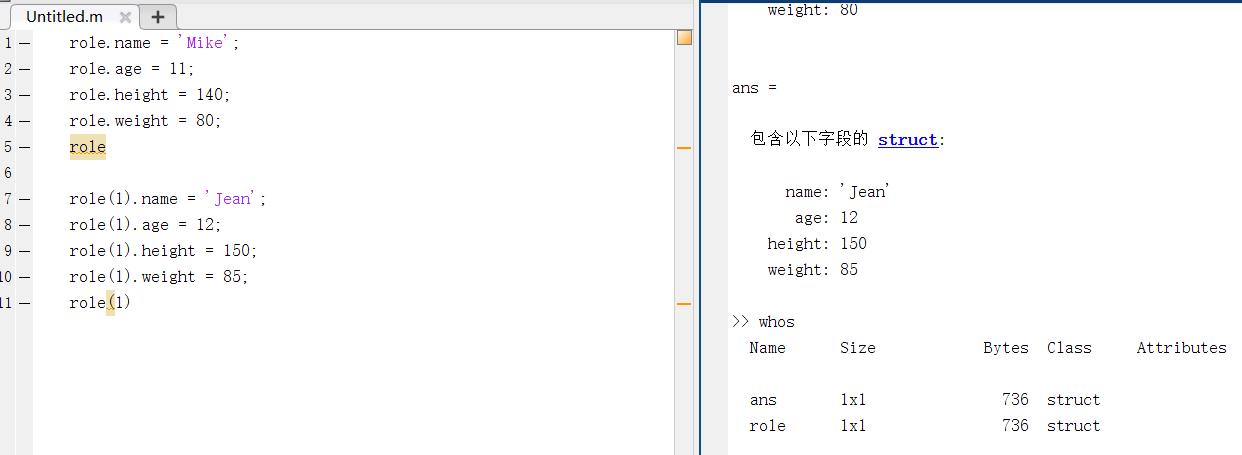
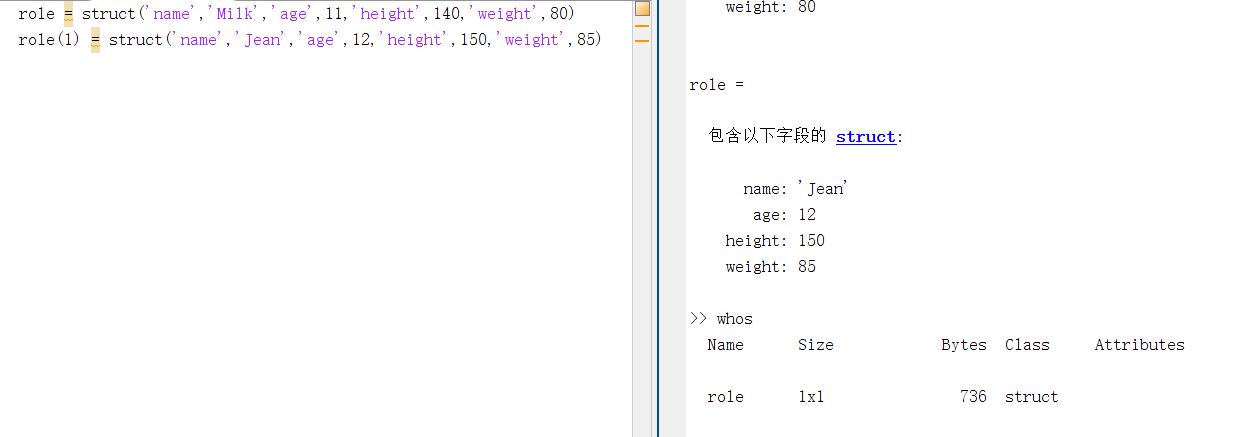
1.直接法产生结构体（指针操作符），连接结构体变量名与属性名（struct_name.field=value）

2.使用struct函数产生结构体，结构体变量名=struct(属性名1,属性值1,属性名2,属性值2,…)（struct_name = struct(‘field1’,value1,‘field2’,value2,…)）

2.函数

函数	说明
struct	创建结构数组
isfield	判断是否存在该字段
deal	把输入处理成输出
getfield	获取结构中指定字段的值
setfield	设置结构数组中指定的字段的值
struct2cell	结构数组转化成元胞数组
isstruct	判断某变量是否是结构类型
fieldnames	获取结构的字段名
rmfield	删除结构的字段(不是字段内容)

1.8.函数句柄

将一个函数封装成一个变量，使其能够像其他变量一样在程序的不同部分传递

1.声明

1.句柄名 = @函数名
2.句柄名 = str2func(‘函数名’)
2.句柄名 = @(参数列表)单行表达式

2.调用

1.句柄名(x1,x2,…,xm)
2.[y1,y2,…,yn]=feval(句柄名,x1,x2,…,xm)

2.数值矩阵运算

2.1.矩阵的建立

1.矩阵名 = [第一行元素；第二行元素；…]
    间隔符：空格或逗号

2.使用M文件建立

1.启动有关编辑程序或MATLAB文本编辑器（脚本），并输入待建矩阵
2.把输入的内容以纯文本方式存盘（设文件名（自定义）为mymatrix.m）
3.在MATLAB命令窗口中输入mymatrix，调用矩阵

3.利用其他文本编辑器建立矩阵

1.编辑一个文本文件
2.将该文本装入dat或txt等格式的文件
3.需要该文件，可以在命令窗口输入load 文件名.后缀

4.建立大矩阵
    使用[ ]连接各个小矩阵（;表示垂直连接，，表示水平连接）

2.2.数值矩阵运算

2.2.1.建立向量

1. e1:e2:e3           %初值:步长:终止值
2. linspace(a,b,n)     %linspace(初始元素,终止元素,元素数)
   a:(b-a)/(n-1):b

2.2.2.矩阵元素的使用

1.a(1,1)    %下标引用
2.a(3)      %序号引用

矩阵元素在MATLAB中按列存储，序号与下标一一对应：
    对于m*n矩阵a，a(i,j)的序号为(j-1)*m+i

2.2.3.矩阵拆分

表达式	说明
A(i,j)	第i行第j列的元素
A(i,:)	第i行所有元素
A(:,j)	第j列所有元素
A(i:j,:)	第i到j行所有元素
A(i:j,m:n)	第i行到j行与第m列到n列所有元素
A(i:end,:)	第i行到最后一行的所有元素

2.2.4.矩阵元素的删除

使用[ ]空矩阵进行删除操作

1.a(1,:)    %删除第一行元素
2.a(3)      %删除序号为3的元素

2.2.5.矩阵变换函数

函数	说明	函数	说明
fliplr(a)	左右翻转	flipud(a)	上下翻转
rot90(a)	逆时针旋转90°	rot90(a,k)	逆时针旋转k*90°
reshape(a,m,n)	将矩阵元素按列方向进行重组 必须满足m*n=a的元素数

2.2.6.常见生成函数

函数	说明
zeros(m,n)	生成一个 m 行 n 列的零矩阵，m=n 时可简写为 zeros(n)
ones(m,n)	生成一个 m 行 n 列的元素全为 1 的矩阵, m=n 时可写为 ones(n)
eye(m,n)	生成一个主对角线全为 1 的 m 行 n 列矩阵, m=n 时可简写为 eye(n)，即为 n 维单位矩阵
diag(X)	若 X 是矩阵，则 diag(X) 为 X 的主对角线向量 若 X 是向量，diag(X) 产生以 X 为主对角线的对角矩阵
tril(A)	提取一个矩阵的下三角部分
triu(A)	提取一个矩阵的上三角部分
rand(m,n)	产生 0～1 间均匀分布的随机矩阵 m=n 时简写为 rand(n)
randn(m,n)	产生均值为0，方差为1的标准正态分布随机矩阵，m=n 时简写为 randn(n)
magic(m)	每行每列以及主、副对角线上各n个元素之和都相等

2.2.7.矩阵算法

1. 查看矩阵大小

size(a)      %列出矩阵A的行数和列数
size(a,1)    %列出矩阵A的行数
size(1,a)    %列出矩阵A的列数

2. 查看长度

length(x)    %返回向量x的长度
length(a)    %max(size(A))

3. 转置

a’         %共轭转置
a.^       %普通转置
conj(a)   %共轭矩阵

4. 加减乘除

+ - %两个矩阵维数相同
     %矩阵对应元素相加减
     %一个标量与矩阵每个元素加减

*    %矩阵1的列数= 矩阵2的行数
      %m*n矩阵与n*p矩阵相乘
     %结果为m*p矩阵

/ \\ %B/A(右除)A\\B(左除)
     %C = B/A = B*inv(A) C = A\\B = inv(A)*B
^   %m^n，m为方阵，n为标量
     %每个元素的n次方

5. 逆矩阵

逆矩阵
inv(A)           %A的逆矩阵
A*B = B*A = 1   %A、B为互逆阵，1为单位矩阵

伪逆
pinv(A)
    如果矩阵A不是一个方阵，或者A是一个非满秩的方阵时，矩阵A没有逆矩阵，但可以找到一个与A的转置矩阵A’同型的矩阵B，使得A*B*A = B 且 B*A*B = A 此时称矩阵B为矩阵A的伪逆，也称为广义逆矩阵

6. 向量的点积和叉积

dot(a,b)、a'*b、sum(a.*b)    %向量的点积（内积）：两个向量在其中某一个向量方向上的投影的乘积
cross(a,b)                      %向量的叉积（外积）：过两相交向量的交点，垂直于两向量所在平面的向量。二维平面中，两向量叉积的模为由两向量所组成的平行四边形的面积

7. 逻辑运算

&与、|或、~非

8. 矩阵的特殊运算

det(A)       %矩阵行列式：A为方阵
k = rank(A) %矩阵秩运算：矩阵线性无关的行数与列数称为矩阵的秩
eig(A)       %矩阵特征值运算
              %E=eig(A)：返回矩阵A的全部特征值向量E
              %[V,D]=eig(A)：矩阵A的全部特征值构成对角阵D，A的特征向量构成V的列向量
trace(A)    %矩阵的迹：矩阵的迹等于矩阵的对角线元素之和，也等于矩阵的特征值之和

3.多项式及其运算

在 Matlab 中，n 次多项式是用一个长度为 n+1的向量来表示，缺少的幂次项系数为 0

对应的向量

3.1.加减运算

多项式系数向量的加减运算

两个多项式：次数相同，系数向量直接进行加减运算；次数不同，低次多项式的高次项补0，再进行加减

3.2.乘除运算

多项式系数向量的乘除运算

k = conv(p,q)

多项式系数向量的除法运算

[k,r]=deconv(p,q)
k返回的是多项式p除以 q的商
r是余式

3.3.求导运算

k = polyder(p)      %多项式p的导数
k=polyder(p,q)      %p*q的导数
[k,d]=polyder(p,q) %p/q 的导数，k是分子，d是分母

3.4.多项式求值

1. 代数多项式求值

y=polyval(p,x)    %计算多项式p在x点的值
注意： 当x为向量或矩阵，则采取数组运算（点运算）

分别取 x=2和一个2x2矩阵，求 p(x)在 x处的值

2. 矩阵多项式求值

Y=polyvalm(p,X)    %以方阵X为自变量，计算多项式的值，采用矩阵运算

polyvalm(p,A)=2*A*A*A - A*A + 3*eye(size(A));
polyval(P,A)=2*A.*A.*A - A.*A + 3*ones(size(A))

3.5.多项式求根

x=roots(p)    %若p是n次多项式，则输出x为包含p=0的n个根的n维向量(所有零点)

求p(x)的零点

3.6.部分分式展开

[r,p,k]=residue(b,a)    %求解多项式b(s)/a(s)的部分分式展开，返回留数r、极点p（分母为0）、直径向量k，a、b分别是分母和分子多项式的系数向量

如果分母多项式a(s)不含重根，则两个多项式可写成如下形式：

其中，极点pi，留数ri，直项k(s)，如果b的次数低于a的次数，则直项为空

分解式子F(s)=b(s)/a(s)=(−4s+8)/(s^2+6s+8)

3.7.求解方程

1. 非线性方程求解

fzero(f,x0)    %求方程f=0在x0附近的根

说明：
    1.方程可能有多个根，但fzero之给出离x0最近的一个根；
    2.若x0是一个标量，则fzero先找出一个包含x0的区间，使得f在这个区间两个端点上的值异号，然后再在这个区间内寻找方程f=0的根；如果找不到这样的区间，则返回 NaN；
    3.若x0是一个2维向量，则表示在[x0(1),x0(2)]区间内求方程的根，此时必须满足f在这两个端点上的值异号；
    4.由于fzero是根据函数是否穿越横轴来决定零点，因此它无法确定函数曲线仅触及横轴但不穿越的零点，如|sin(x)|的所有零点；
    5.函数中的f是一个函数句柄，可通过以下任一方式给出
        字符串形式：fzero(‘x^3-3*x+1’,2);
        通过@调用的函数句柄：fzero(@sin,4);
    6.f不能用符号表达式

2. 符号方程求解

s=solve(f,’v’)    %求方程关于指定自变量的解；
s=solve(f)         %求方程关于默认自变量的解。
solve(f1,f2,...,fN,’v1’,’v2’,...,’vN’)%求解由 f1,f2,…,fN 确定的方程组关于 v1, v2,…,vN 的解

注意： 其中f可以是用字符串表示的方程，或符号表达式；若f 中不含等号，则表示解方程 f=0

求解单个方程：x^2-1=0



求解方程组

3.线性方程求解

linsolve(A,b)    %解线性方程组Ax=b

4.字符串变量与符号矩阵

4.1.数值运算与符号运算

数值计算：
    参与运算的变量是被赋值的数值变量，用于数值的存储和各种数值的计算
符号运算：
    参与运算的变量是符号变量,用于形成符号表达式,进行各种运算,给出解析表达式的结果

求根：x^2 + 2*x -3
数值计算：

符号计算：

4.2.创建符号变量和表达式

syms var1 var2 … varn  %变量间用空格分隔，一次定义多个变量
var=sym(’x’)            %x可以是字符、字符串、表达式，创建一个符号数组或矩阵

4.3.创建符号矩阵

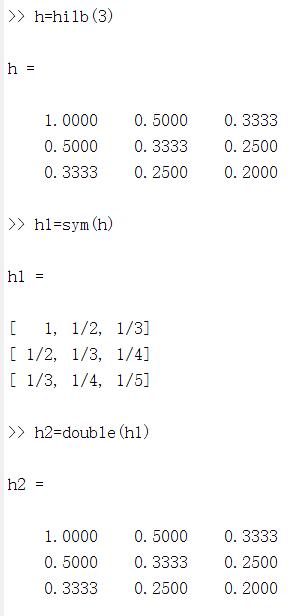
使用sym和syms函数直接输入创建符号矩阵，可以与数值矩阵相互转换

sym(x)      %数值矩阵转换为符号矩阵
double(x)  %符号常量矩阵转换为数值矩阵

4.4.默认符号变量的查询

symvar(f)    %对函数f的默认自变量进行查询，按字母顺序排列表达式f中全部自变量
symvar(f,n)  %按最接近变量x的顺序排列f中的前n个自变量

注意： i,j表示虚数单位，因此不能作为自变量

4.5.符号表达式的化简

factor(S)    %因式分解
expand(S)    %符号表达式的展开
collect(S,n) %符号表达式的同类项合并

simplify(S)    %符号表达式的化简

[n,d]=numden(S)    %符号表达式的分式通分,将符号表达式转换为分子和分母都是整系数的最佳多项式,n分子,d 分母
对表达式进行通分

horner(S)    %符号表达式的嵌套式重写
对表达式进行嵌套形式重写

4.6.符号表达式的替换

[Y,SIGMA]=subexpr(S,SIGMA)    %将表达式中重复出现的字符串用变量代替,SIGMA(表达式S中重复出现的字符串)，Y返回替换后的结果

R=subs(S,old,new)    %用指定符号替换符号表达式中的某一特定符号，当变量new是数值形式时，所显示的结果虽然是数值，但它事实上仍然是符号变量

4.7.符号极限

注意： ∞在MATLAB中表示为inf

4.8.符号微分

diff(S)       %对默认变量x,dS/dx
diff(S,v)    %对默认变量v,dS/sv
diff(S,n)    %对默认变量x,d^nS/dxn

4.9.符号积分

int(S)    %对默认自变量x求积分
int(S,v)    %对自变量v求积分
int(S,a,b)    %对默认自变量x

int(S,v,a,b)    %对自变量v

4.10.符号求和

symsum(S)

symsum(S,v)

symsum(S,a,b)

symsum(S,v,a,b)

5.有关复变函数的函数

函数	说明
real(x) imag(x)	返回复数x的实部 返回复数x的虚部
conj(x)	返回复数x的共轭复数
abs(x) angle(x)	返回复数x的模 返回复数x的辐角
sqrt(x)	返回复数x的平方根值
* / ^	乘 除 幂

---