几数之和两种题型总结(hash表二分双指针)

Posted 2021-07-12 C_YCBX Py_YYDS

几数之和的总结

1. 如果是问几数之和各个数的组合数，如之前的三数之和那题，一般是用到二分或者双指针这种能够得到具体数字情况的方法来降低循环的层数。(与数组元素的具体值相关)
2. 如果是问几数之和中符合情况的个数，一般都是用hash表降低循环层数，此时我们只需要关注答案的次数即可。(和数组下标相关)

显然此题属于第二种情况。

如何用hash表降低循环层数？

题目

• 比如对于这题，原本需要四个循环才能枚举出所有的四数之和情况，此题需要满足的条件为:
• A[i]+B[j]+C[k]+D[l]=0 =>A[i]=-(B[j]+C[k]+D[l]) =>A[i]+B[j]=-(C[k]+D[l])

1. 对于第一种表达式，我们需要套用四层循环枚举 O(n^4)
2. 对于第二种需要两个并列的循环枚举(一层和三层循环) O(n^3)
3. 对于第三种需要两种并列的循环枚举(两层和两层循环) O(n^2)

对于第一种我们直接四层循环便能判断答案，对于第二种和第三种，我们需要把其中的一个循环结果保存到hash表中才能够进行判断。

接下来写代码应该就很简单了。

class Solution {
public:
    int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
        unordered_map<int,int>hash;
        int res = 0;
        int n =nums1.size();
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                hash[nums1[i]+nums2[j]]++;
            }
        } for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                auto it = hash.find(-(nums3[i]+nums4[j]));
                if(it!=hash.end()){
                    res += it->second;
                }
            }
        }
    return res;
    }
};

如何用双指针降低循环层数(以三数之和为例)

题目：

读题：注意不重复这三个字。

题目解析

我第一时间想到的竟然是排序二分查找优化。。。
后面看了答案才知用双指针，故理解了双指针和二分查找的不同的妙用。

二分查找：是在有序数组中利用左右下标查找一个target的最佳方法，O(logn).
双指针：在有序数组(不局限于数组)中利用左右指针所指的两个数来查找两数之和是否等于target的最佳方法，O(n).

综上分析，故此题三数之和用双指针法优化是最好的结果。O(n^3)=> O (n ^2).

具体做法是，固定外层循环得到target = 0 - nums[i];
而后就是双指针从nums.size-i到num.size-1来查找两数之和等于target的数。

那么这又涉及了另外一个问题：去重。

关于去重，在数组有序的时候，完全可以通过判断后续元素如果碰到相同的就跳过来解决。
面对双指针的去重，也是一样的方法，在每次双指针找到答案后，由于顺序是有序的，所以同样可以通过，循环的left++和right–直到数据不在和前一个重复，当left=right时那就说明所有结果都列举完了。
即便不去重，我们的双指针，也是根据从小到大的排序规律，需要将left++，right–，因为一旦发现target，那么下一个target的范围就被确定在(left,right)之间(因为有序，这个可以自己举例证明)。

图解：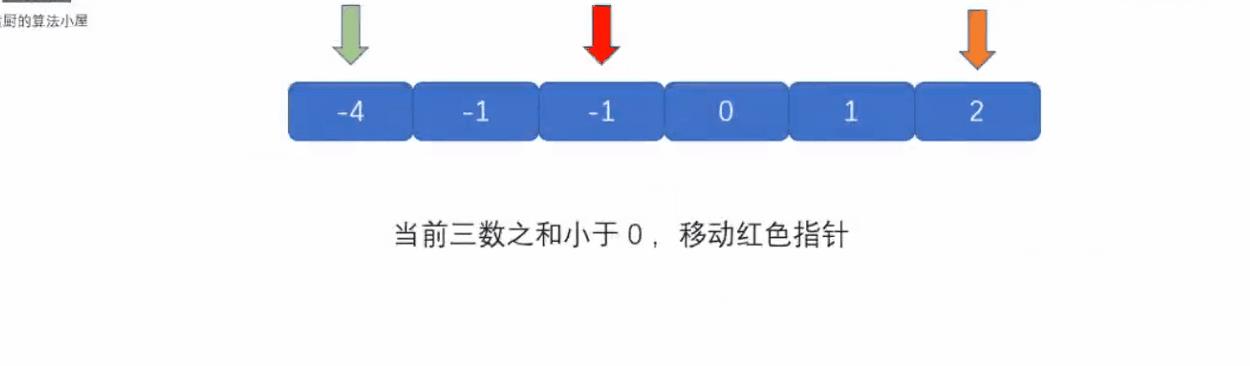

代码：

class Solution {
public:
vector<vector<int>>res;
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        for(int i=0;i<nums.size();i++){
            //由于有序，若后面直接重复，continue即可
            if(i>0&&nums[i]==nums[i-1])
                continue;
            int target = 0 - nums[i];
            //双指针处理
            int left = i+1;int right = nums.size()-1;
            while(left<right){
                int sum = nums[left]+nums[right];
                if(sum == target){
                    res.emplace_back(vector<int>{nums[i],nums[left],nums[right]});
            //由于每次如果不去重，双指针的下一个target范围也是在(left,right)之间。
        //去重则是在此基础上通过判断left所指的数是否曾经选择过，right所指的数是否曾经选择过。
                    while(left<right&&nums[left]==nums[++left]);
                    while(left<right&&nums[right]==nums[--right]);
                }
                else if(sum > target){
                    right--;
                }
                else
                    left++;
            }
            
        }
        return res;
    }
};