学以致用--确定有穷状态自动机(DFA）

Posted 2021-07-12 C_YCBX Py_YYDS

文章目录

• 题目
• 题目解析
• 最后的解题代码

题目

题目解析

看完题目，很明显的给出字符串，要求判断该字符串是否可接受，这就很明显了，形式语言与自动机恰好有这样的题目，给出可输入变量的集合，然后构造一个可接受某种语言的自动机，对于这道题的要求就相当于对可接受语言的描述，而给出的字符串就是随机给出的语言，我们只需要构造好对应语言的DFA就可以通过DFA确定该语言是否可接受。

好了理论的课本知识分析到此为止，具体的代码如何敲呢？我们可以先画出自动机的状态转移图，根据状态转移图得出对应的状态转移表，故可以通过数组来描述该表，然后把对应的字符换成对应的输入编号(列标)，通过自动机扫描完整个字符串变可以通过最后到达的状态是否可接受来判断字符串是否可接受即可。

1. 根据题意画出状态转移图。
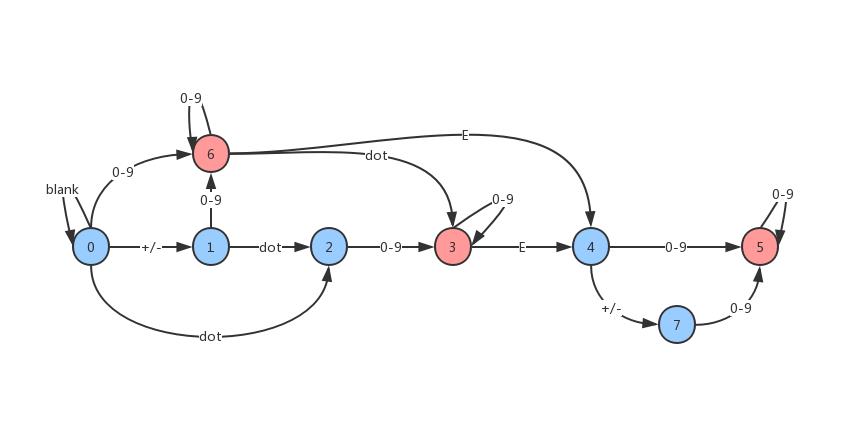
2. 将状态转移图转化为状态转移表以方便数组表示。
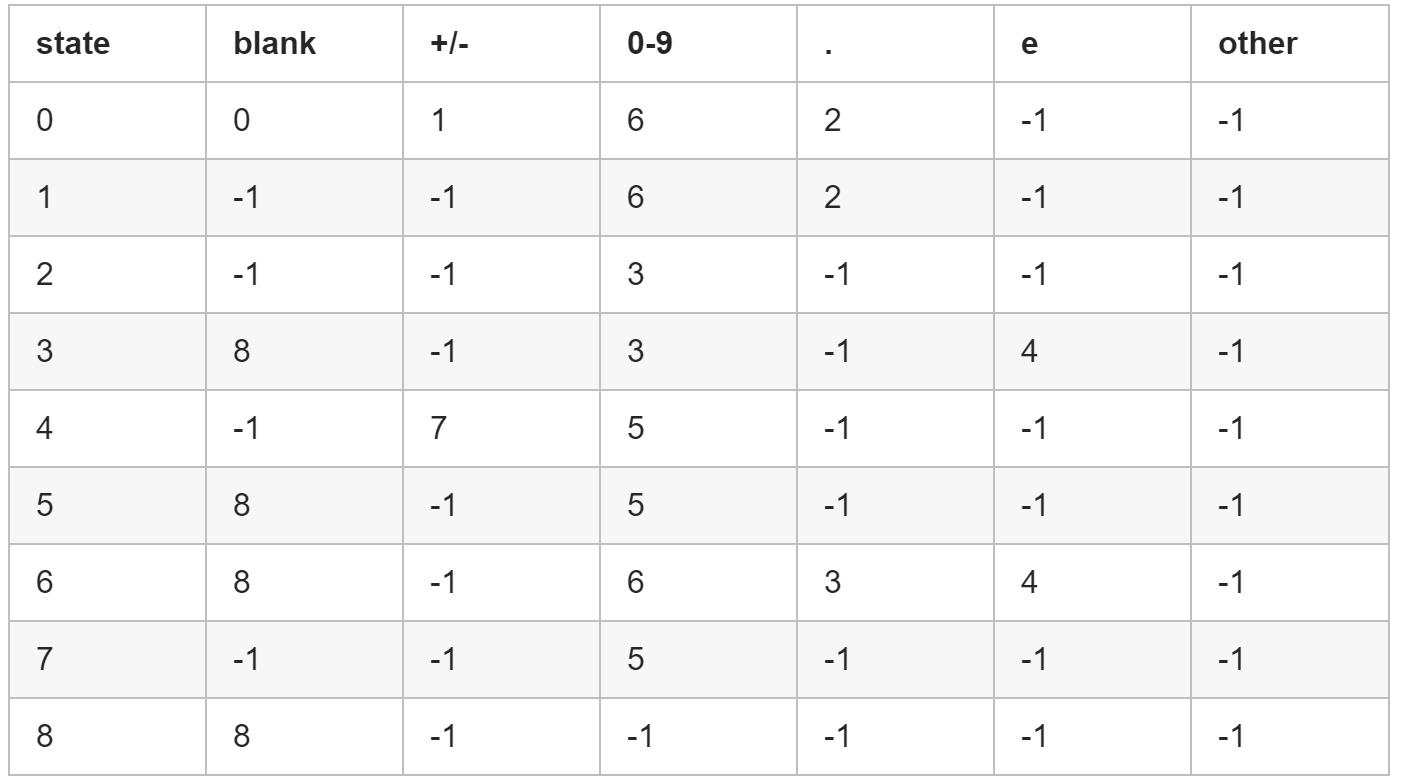
3. 将状态转移表用数组表示

vector<vector<int> > transfer({
                {0,  1,  6,  2,  -1, -1},
                {-1, -1, 6,  2,  -1, -1},
                {-1, -1, 3,  -1, -1, -1},
                {8,  -1, 3,  -1, 4,  -1},
                {-1, 7,  5,  -1, -1, -1},
                {8,  -1, 5,  -1, -1, -1},
                {8,  -1, 6,  3,  4,  -1},
                {-1, -1, 5,  -1, -1, -1},
                {8,  -1, -1, -1, -1, -1},
                });

4. 通过读取字符来进行自动机的状态转移。

for(int i = 0; i < n; ++i){
            state = transfer[state][_make(s[i])];
            if(state < 0) return false;
        }

5. 查看最后停下的状态是否可接受。

return finals[state];

最后的解题代码

class Solution {
public:
    bool isNumber(string s) {
        if(s.empty()) return false;
        int n = s.size();

        int state = 0;
//在整个数的首部和尾部加上空格都是合法的，所以单独又开辟出一个8状态用于处理后面有空格的情况
        vector<bool> finals({0, 0, 0, 1, 0, 1, 1, 0, 1}); // 合法的终止状态

//用二维数组画状态表，行标代表状态，列标表示在该状态下输入的变量，根据输入和当前状态来进行状态跳转(0状态为开始状态)
        vector<vector<int> > transfer({
                {0,  1,  6,  2,  -1, -1},
                {-1, -1, 6,  2,  -1, -1},
                {-1, -1, 3,  -1, -1, -1},
                {8,  -1, 3,  -1, 4,  -1},
                {-1, 7,  5,  -1, -1, -1},
                {8,  -1, 5,  -1, -1, -1},
                {8,  -1, 6,  3,  4,  -1},
                {-1, -1, 5,  -1, -1, -1},
                {8,  -1, -1, -1, -1, -1},
                });
        //开始根据输入的变量进行状态转移
        for(int i = 0; i < n; ++i){
            state = transfer[state][_make(s[i])];
            if(state < 0) return false;
        }//检查是否为合法状态(状态机是否接受该语言)
        return finals[state];
    }

private:
    int _make(const char& c){
        switch(c){
            case ' ': return 0;
            case '+': return 1;
            case '-': return 1;
            case '.': return 3;
            case 'e': return 4;
            case 'E': return 4;
            default: return _number(c);
        }
    }

    int _number(const char& c)
    {
        if(c >= '0' && c <= '9')
            return 2;
        else
            return 5;
    }
};