(采油区域)二维前缀和+动态规划关系+分类讨论

Posted 2021-07-12 C_YCBX Py_YYDS

文章目录

• 题目
• 逐步解析
• • 第一步：二维前缀和处理
  • 第二步：根据二维前缀和得出某k区间和
  • 第三步：以第二步为基础得出任意一点的左\\右上角、左\\右下角、任意两列\\两行的最大k区域和值
  • 最后一步：枚举得到答案
• 代码汇总得出答案

题目

oj平台

---

逐步解析

第一步：二维前缀和处理

什么是前缀和？比如对于一个一维数组 nums,他的前 i 个数的总和就是下标i的前缀和,即 sum[i] 表示前i个 nums 数组元素之和。

一维数组前缀和有以下关系：$sum[i]=sum[i-1]+nums[i-1]$

• 现在我们对前缀和有了一定的了解，那么二维数组的前缀和该如何表示呢？
  我直接给出结论：$sum[i][j]=nums[i][j]+sum[i-1][j]+sum[i][j-1]$

这个关系对应的位置实际上就是在 [i,j] 矩阵的基础上，加上左边和上面，最后不断递推便可得到二维的前缀和

现在给出前缀和处理代码：

//求出二维前缀和
for(int i=1;i<=n;i++){
    for(int j=1;j<=m;j++){
        int t;cin>>t;
        sum [i][j] = sum [i-1][j] + sum [i][j-1] - sum [i-1][j-1] + t;
    }
}

---

第二步：根据二维前缀和得出某k区间和

行和列都为 k 的矩阵(以 [i,j] 为右下角)和都可以表示为：$sum[i][j]-sum[i-k][j]-sum[i][j-k]+sum[i-k][j-k]$(道理很简单自己可以去画图观察)

//用于形成上面这个区间值的函数
int getVal(int i,int j){
    return sum[i][j] - sum[i-k][j] - sum[i][j-k] + sum[i-k][j-k];
}

后面求和都用到该函数

---

第三步：以第二步为基础得出任意一点的左\\右上角、左\\右下角、任意两列\\两行的最大k区域和值

量	$lu[i][j]$	$ld[i][j]$	$ru[i][j]$	$rd[i][j]$	$ver[i][j]$	$hor[i][j]$
含义	左上角最大 k∗k矩阵数字和	左下角最大 k∗k 矩阵数字和	右上角最大k*k 矩阵数字和	右下角最大 k*k 矩阵数字和	i 到 j 列最大 k*k 矩阵数字和	i 到 j 行最大 k*k 矩阵数字和

实现代码：

//求出某个点的左上角最大k区域值
for(int i=k;i<=n;i++){
    for(int j=k;j<=m;j++){
        lu[i][j] = max(max(lu[i][j-1],lu[i-1][j]),getVal(i,j));
    }
}

//求出某个点左下角最大k区域值
for(int i=n-k+1;i>=1;i--){
    for(int j=k;j<=m;j++){
        ld[i][j] = max(max(ld[i][j-1],ld[i+1][j]),getVal(i+k-1,j));
    }
}

//求出右上角最大k区域值
for(int i=k;i<=n;i++){
    for(int j=m-k+1;j>=1;j--){
        ru[i][j] = max(max(ru[i][j+1],ru[i-1][j]),getVal(i,j+k-1));
    }
}

//求出右下角最大k区域值
for(int i=n-k+1;i>=1;i--){
    for(int j=m-k+1;j>=1;j--){
        rd[i][j] = max(max(rd[i][j+1],rd[i+1][j]),getVal(i+k-1,j+k-1));
    }
}

这里开始处理是真滴妙！！！，由于无法直接得出任意两行或者两列的最大 k 区域值的答案，可以先计算 [i,i+k-1]，由于这个区间没次都只是计算 i+1 之后的框定，所以当你计算完这个后，再把框选的长度调整为 k+1 ，则可以得到 k+1 跨度的k 区域最大值答案，以此类推完成计算 k+1 跨度后继续计算 k+2 …由于每次都是用的新的东西取值不会覆盖之前的区间跨度答案，所以便得到了任意区间跨度的k区间最大值答案！！

//求出任意两列\\两行间的最大k区域值
//此处仅处理[i,i+k-1](i<=n-k+1)的情况
for(int i=1;i<=m-k+1;i++){
    for (int j = 1; j<=n-k+1; j++){
        ver[i][i+k-1] = max(ver[i][i+k-1],getVal(j+k-1,i+k-1));
    }
}
for(int i=1;i<=n-k+1;i++){
    for (int j = 1; j<=m-k+1; j++){
        hor[i][i+k-1] = max(hor[i][i+k-1],getVal(i+k-1,j+k-1));
    }
}

//开始由[i,i+k-1]递推[i,i+k-1+...]
for(int len = k+1;len<=m;len++){
    for(int i=1,j=i+len-1;j<=m;j++,i++){
        ver[i][j] = max(ver[i][j-1],ver[i+1][j]);
    }
}
for(int len = k+1;len<=n;len++){
    for(int i=1,j=i+len-1;j<=n;j++,i++){
        hor[i][j] = max(hor[i][j-1],hor[i+1][j]);
    }
}

---

最后一步：枚举得到答案

由于是要分为三个区域取k矩阵，所以一共可以分为以下六种情况进行枚举。

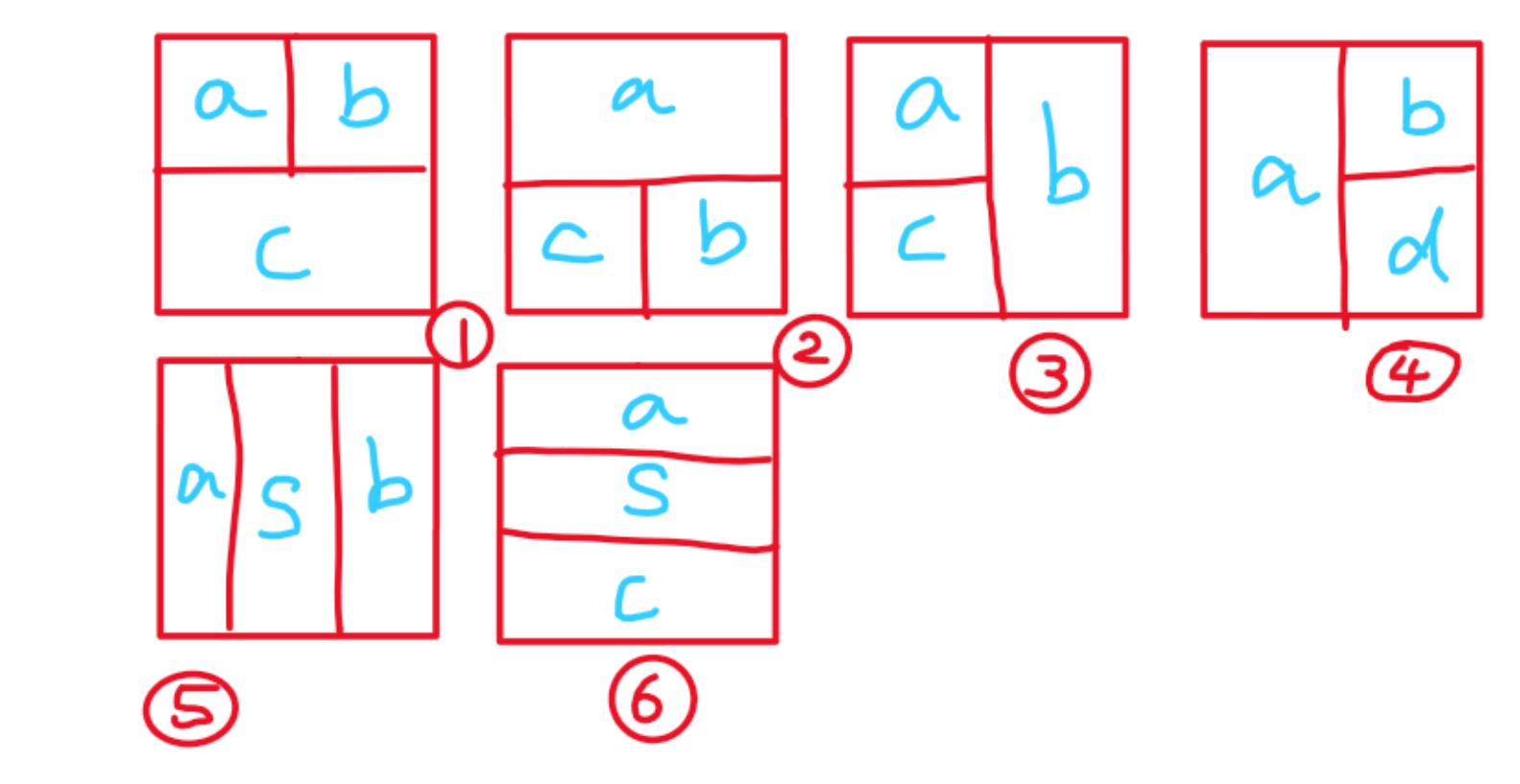
• 对于前四种情况可以通过前面求出的某点的左上角、右上角最大值等等把以上四种情况的最大值都枚举。
  如下：

  int ans = 0;
  //前四种分割方式      (i,j相当于一个点)
  	for(int i=1;i<=n;i++) {
  		for(int j=1;j<=m;j++) {
  			ans=max(ans,hor[i+1][n]+lu[i][j]+ru[i][j+1]);
  			ans=max(ans,hor[1][i]+ld[i+1][j]+rd[i+1][j+1]);
  			ans=max(ans,ver[j+1][m]+lu[i][j]+ld[i+1][j]);
  			ans=max(ans,ver[1][j]+ru[i][j+1]+rd[i+1][j+1]);
  		}
  	}
  

• 对于后面两种也可以通过将 i,j 当成两条线的形式不断枚举。
  如下：

  //另外的两种分割方式    (i,j相当于两条线)
  	for(int i=1;i<=n;i++) {
  		for(int j=i+1;j<=n;j++) {
  			ans=max(ans,hor[1][i]+hor[i+1][j]+hor[j+1][n]);
  		}
  	}
  	for(int i=1;i<=m;i++) {
  		for(int j=1;j<=m;j++) {
  			ans=max(ans,ver[1][i]+ver[i+1][j]+ver[j+1][m]);
  		}
  	}
  //最后得到的ans便是枚举出的最大值！
  

---

代码汇总得出答案

#include<bits/stdc++.h>
using namespace std;
const int size = 1510;
int n,m,k;
int sum[size][size] = {0};
int lu[size][size] = {0};
int ld[size][size] = {0};
int ru[size][size] = {0};
int rd[size][size] = {0};
int ver[size][size] = {0};
int hor[size][size] = {0};
//用于形成上面这个区间值的函数
int getVal(int i,int j){
    return sum[i][j] - sum[i-k][j] - sum[i][j-k] + sum[i-k][j-k];
}
//为了效率直接用getchar封装一个取值函数
int read() {
	char ch=getchar();
	int f=1,x=0;
	while(ch<'0'||ch>'9') {
		if(ch=='-')
			f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9') {
		x=x*10+ch-'0';
		ch=getchar();
	}
	return f*x;
}
int main(){
cin>>n>>m>>k;
//求出二维前缀和
for(int i=1;i<=n;i++){
    for(int j以上是关于(采油区域)二维前缀和+动态规划关系+分类讨论的主要内容，如果未能解决你的问题，请参考以下文章
 
 APIO2009 采油区域
 算法动态规划 ④ ( 动态规划分类 | 坐标型动态规划 | 前缀划分型动态规划 | 前缀匹配型动态规划 | 区间型动态规划 | 背包型动态规划 )
 算法动态规划 ④ ( 动态规划分类 | 坐标型动态规划 | 前缀划分型动态规划 | 前缀匹配型动态规划 | 区间型动态规划 | 背包型动态规划 )
 304. 二维区域和检索 - 矩阵不可变（动态规划）
 经典动态规划
 动态规划 解决二维最大子序和问题---滚动数组