给定数额买物品最多数量的三种解法(计数排序贪心dp)

Posted 2021-07-12 C_YCBX Py_YYDS

文章目录

• 题目
• 解法一(没错我开始竟然想到的是背包)
• 解法二：朴素排序+贪心
• 解法三：计数排序+贪心

题目

oj平台

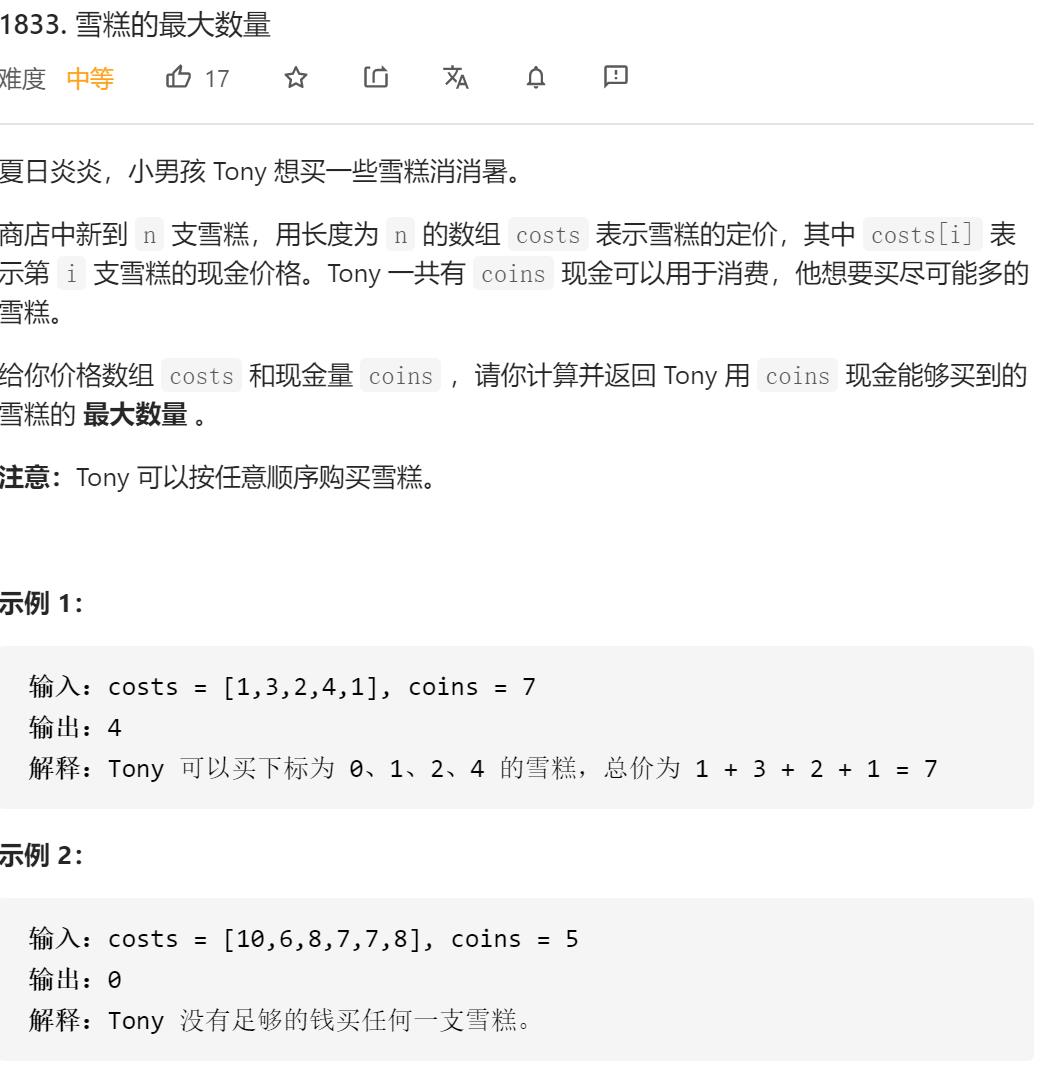
解法一(没错我开始竟然想到的是背包)

可惜O(n^2)复杂度终究过不了(害我还优化了蛮久)

class Solution {
public:
    int maxIceCream(vector<int>& costs, int coins) {
        int n = costs.size();
        int dp[coins+1];memset(dp,0,sizeof(dp));
        for(int i=1;i<=n;i++){
            for(int j = coins;j>=costs[i-1];j--){
                    dp[j] = max(dp[j],dp[j-costs[i-1]]+1);
            }
        }
        return dp[coins];
    }
};

解法二：朴素排序+贪心

O(n*logn)效率还行

class Solution {
public:
    int maxIceCream(vector<int>& costs, int coins) {
        sort(costs.begin(),costs.end());
        int res = 0;
        long long sum = 0;
        for(int i=0;i<costs.size();i++){
            sum += costs[i];
            if(sum<=coins)
                res++;
            else 
                break;
        }
        return res;
    }
};

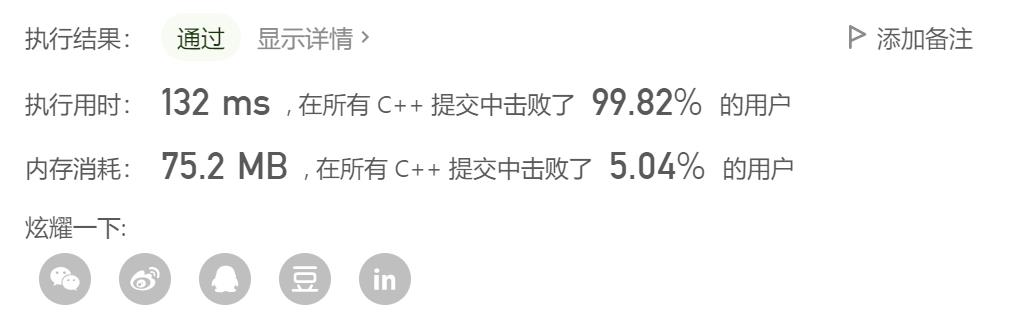
解法三：计数排序+贪心

这应该是此题C++效率的天花板了吧。。

class Solution {
public:
    int maxIceCream(vector<int>& costs, int coins) {
        //找最小值和最大值再建表，有利于内存的节省
        int mx = *max_element(costs.begin(),costs.end());
        int mn = *min_element(costs.begin(),costs.end());
        int mp[mx-mn+1];memset(mp,0,sizeof(mp));
        //建立计数表
        for(int i=0;i<costs.size();i++)
            mp[costs[i]-mn]++;
        long long sum = 0;
        long long res = 0;
        for(int i=0;i<=mx-mn;i++){
            long long tmp = sum;
            sum += (long long)mp[i]*(mn+i);
            if(sum<=coins)
                res+=mp[i];
            else{
    //如果不够直接硬凑，向下取整嘛
                int&& target = coins - tmp;
                res += target/(i+mn);
                break;
            }
        }
        return res;
    }
};