详细分析二分查找算法

Posted 2021-07-11 猿猿HHH

假设一张0.001cm的纸可以无限次数折叠，那它折叠多少次的高度可以从地面到达月球？
答案是log（3.510^（1000001000*100/0.001))，结果约等于45。这结果是否与你的感觉有所差距？
因此，可想而知二分查找算法中，折半查找的思路的效率有多高了。现在我们就来详细讨论下二分查找算法。

算法具体思路

现在给出一个排序的数组，例如是{1，2，3，4，5，6，7，8，9}，查找出元素3在数组中的下标？
思路一：最直接的办法—遍历，从数组第一个元素遍历到数组最后一个元素，找出3，显然，时间复杂度为O（n）。可是，题目给出的是排序的数组，凭感觉就知道这肯定不是最优解。
思路二：题目给出的是按照升序排列后的数组，那可否采用折中的办法，用数组中间的元素与目标值比较，把数组不断地进行对半拆分呢？这就是二分查找算法，显然最坏情况下，执行的次数为logn，该算法的时间复杂度为O（logn）。
思路二具体代码如下：

class Main{
	public int find(int[] nums,int target){
		int left = 0,right = nums.length-1;
		while(left<=right){
			int mid = left + (right-left)/2;
			if(nums[mid]==target) return mid;
			else if(nums[mid]<target) left = mid+1;
			else right = mid-1;
		}
		return -1;
	}
}		

注意，计算数组中间元素下标的时候，一般采用“int mid = left + (right-left)/2”，而不是“int mid = （left + right)/2”，防止“mid”越界，超越int的范围发生错误。

进阶版本，把数组旋转，如下面例题：

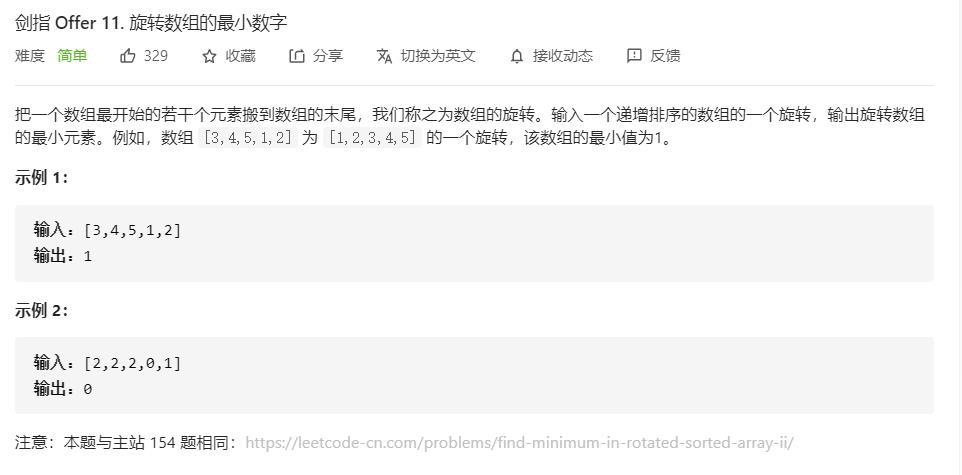
大体思路：中间元素与右指针比较，拆分数组时，舍弃右半数组的话中间指针保留，中间元素与右指针元素相等的情况，右指针减一。

实现代码：

class Solution {
    public int minArray(int[] numbers) {
        int left = 0,right = numbers.length-1;
        while(left<right){
            int mid = left+((right-left)>>2);
            if(numbers[mid]>numbers[right]) left = mid+1;
            else if(numbers[mid]<numbers[right]) right = mid;
            else right--;
        }
        return numbers[left];
    }
}

提交结果：