面向对象程序设计（荣誉）实验四 deque,stack,queue

Posted 2021-07-11 上山打老虎D

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了面向对象程序设计（荣誉）实验四 deque,stack,queue相关的知识，希望对你有一定的参考价值。

1.双向队列(deque)

题目描述

双向队列只能在队尾和队头做出队，入队的操作。

现在给你一系列的操作，请输出最后队列的状态。

命令格式：

LIN X X表示一个整数，命令代表队头进队操作；

RIN X 表示X队尾进队操作；

ROUT 表示队尾删除一个元素的操作，当队列为空时，命令不合法；

LOUT 表示队头删除一个元素的操作，当队列为空时，命令不合法。

输入

第一行包含一个整数M(M<=10000)，表示有M个操作；
以下M行每行包含一条命令；
命令可能不合法，对于不合法的命令，请在输出中处理

输出

输出的第一行包含队列进行了M次操作后的状态，从左往右输出，每两个之间用空格隔开，最后也有空格；若队列为空，输出EMPTY。
以下若干行处理不合法的命令（如果存在）；
对于每一条不合法的命令，请输出一行X ERROR
其中X表示是第几条命令

样例输入

8
LIN 5
RIN 6
LIN 3
LOUT
ROUT
ROUT
ROUT
LIN 3

样例输出

3
7 ERROR

题解

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
deque<int> q;
vector<int> error;
int main(){
	int m;
	cin >> m;
	for(int i = 1; i <= m; i++){
		string op;int num;
		cin >> op;
		if(op == "LIN"){
			cin >> num;
			q.push_front(num);
		}
		if(op == "RIN"){
			cin >> num;
			q.push_back(num);	
		}
		if(op == "ROUT"){
			if(q.empty()){
				error.push_back(i);
				continue;
			} 
			q.pop_front();
		}
		if(op == "LOUT"){
			if(q.empty()){
				error.push_back(i);
				continue;
			} 
			q.pop_back();
		}
	}
	
	if(q.size() == 0){
		puts("EMPTY");
	}else{
		for(int i = 0; i < q.size(); i++){
			cout<<q[i]<<" ";
		}cout<<endl;
	}
	if(error.size()){
		for(int i = 0; i < error.size(); i++){
		cout<<error[i]<<" ERROR\\n";
		}
	}
}

2.括号匹配(stack)

题目描述

给定一个表达式e，包含各种字符，如字母、数字、运算符、标点、空格和括号()[]{}等, 判断其中括号是否匹配，如是，则返回0, 否则根据错误类型返回1-3:

错误类型包括1、2、3类型：

类型1：

左右括号不匹配，如"(]", “(((]))))”, “((}”,“let {x=a[0)*(b+c); y=b}”

类型2:

发现有左括号不存在与之匹配的右括号，有多余的左括号，如"(", “(([]”, “()(()"

类型3：

发现右括号不存在与之匹配的左括号，有多余的右括号，如")", “())”,"(())”。

输入

第一行输入测试次数

第二行开始输入字符串

输出

如果成功匹配则输出yes

如果不成功则输出no，然后输出类型

样例输入

3
()
(]
(([]

样例输出

yes
no 1
no 2

题解

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;

string str;
int main(){
	int t;
	cin >>t;
	while(t--){
		stack<int> s;
		cin >> str;
		int flag = 0;
		int i;
		for(i = 0; i < str.size(); i++){
			if(str[i] == '('||str[i] == '['||str[i]=='{'){
				s.push(str[i]);	
			}
			if(str[i] == ')'||str[i] == ']'||str[i]=='}'){
				if(s.size() == 0){
					flag = 3;
					break;
				}
				char t = s.top();
				if(str[i] == ')' && t == '('){
					s.pop();continue;
				}
				if(str[i] == ']' && t == '['){
					s.pop();continue;
				}
				if(str[i] == '}' && t == '{'){
					s.pop();continue;
				}
				flag = 1;
				break;
			}
			
		}
		if(s.size() != 0 && flag != 1){ 
				flag = 2;
		}
		if(flag) cout<<"no "<<flag<<endl;
		else cout<<"yes\\n"; 
	}
}

3.田忌赛马(deque)

题目描述

田忌和大王赛马。每人分别有n匹马。给出所有马的速度，田忌可自行决定用第i匹与大王的第j匹马比赛。赢一场积1分，输一次扣1分，平局得0分。田忌赛马最多能得几份？

输入

第一行输入测试次数t

每次测试首先输入每个人马的数量n。

随后两行给出马的速度，第一行为田忌马的速度，第二行为大王马的速度。假设已按速度升序排序。

输出

输出田忌最多能赢的场数。

样例输入

2
3
92 83 71
95 87 74
2
20 20
20 20

样例输出

1
0

题解

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;

string str;
int main(){
	int t;
	cin >>t;
	while(t--){
		int cnt = 0, n, num, my;
		deque<int> other;
		cin >> n;
		for(int i = 0; i < n; i++){
			cin >> num;
			other.push_back(num);	
		}
		for(int i = 0; i < n; i++){
			cin >> my;
			if(my> other.back()){
				cnt++;
				other.pop_back();
			}
			else{
				if(my < other.front()){
					cnt--;
				}
				other.pop_front();
			}
		}
		cout<<cnt<<endl;
	}
}

4.火车站(stack)

题目描述

火车站只有一条铁路，所有的火车都停在那里。所以所有的火车都是从一边进站，从另一边出站。如果A列先进入铁路，然后B列在A列离开之前进入铁路，那么A列在B列离开之前不能离开。下图说明了问题所在。车站里最多有9列火车，所有的火车都有一个ID（编号从1到N），火车按照O1的顺序进入火车，火车是否可以按照O2的顺序驶出。
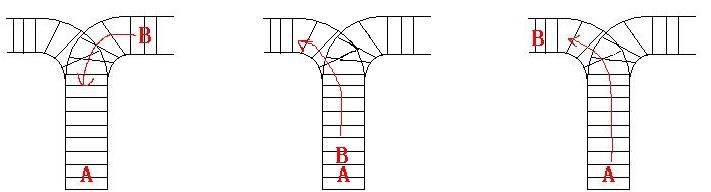
在这里插入图片描述

输入

输入包含几个测试用例。

每个测试用例由一个整数（列车数）和两个字符串组成。两个字符串分别为列车入站顺序和列车出站顺序。

输出

如果不能按照指定顺序出站，输出“No”。

如果可以，输出“Yes”，然后输出出入站顺序（对于进入铁路的列车，应输出“in”，对于出铁路的列车，应输出“out”）。在每个测试用例之后打印一行包含“FINISH”。

样例输入

3
3 123 321
3 abc cab
3 123 123

样例输出

Yes
in
in
in
out
out
out
FINISH
No
FINISH
Yes
in
out
in
out
in
out
FINISH

题解

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
string in,out;
int main(){
	int t,n;
	cin >>t;
	while(t--){
		int flag = 1;
		cin >> n >> in >> out;
		stack<char> s;
		vector<string> ans;
		int pos = 0, i;
		for(i = 0; i < out.size() && pos < out.size(); i++){
			ans.push_back("in");
			s.push(in[i]);
			
			while(s.size() && s.top() == out[pos]){
				pos++;
				s.pop();
				ans.push_back("out");	
			}
		}
		if(pos == i && pos == out.size()){
			puts("Yes");
			for(int i = 0; i < ans.size();i++){
				cout<<ans[i]<<endl;
			}
		}else puts("No");
		puts("FINISH");
	}
}

5.银行单队列多窗口模拟(queue)

题目描述

假设银行有K个窗口提供服务，窗口前设一条黄线，所有顾客按到达时间在黄线后排成一条长龙。当有窗口空闲时，下一位顾客即去该窗口处理事务。当有多个窗口可选择时，假设顾客总是选择编号最小的窗口。

本题要求输出前来等待服务的N位顾客的平均等待时间、最长等待时间、最后完成时间。

输入

输入第1行给出正整数N（≤1000），为顾客总人数；随后N行，每行给出一位顾客的到达时间T和事务处理时间P，并且假设输入数据已经按到达时间先后排好了顺序；最后一行给出正整数K（≤10），为开设的营业窗口数。这里假设每位顾客事务被处理的最长时间为60分钟。

输出

在一行中输出平均等待时间（输出到小数点后1位）、最长等待时间、最后完成时间，之间用1个空格分隔，行末不能有多余空格。

样例输入

9
0 20
1 15
1 61
2 10
10 5
10 3
30 18
31 25
31 2
3

样例输出

6.2 17 62

题解

#include<bits/stdc++.h>

#define P pair<int,int>
using namespace std;
int endtime[15];
int k;

int getID(int start_time, int &minWait) {
    minWait = 0x3f3f3f;
    int id;
    for (int i = 1; i <= k; i++) {
        if (endtime[i] <= start_time) {
            minWait = 0;
            return i;
        }
        if (endtime[i] - start_time < minWait) {
            minWait = endtime[i] - start_time;
            id = i;
        }
    }
    return id;
}

int main() {
    int n, pos, time, len;
    cin >> n;
    queue<P > people;
    for (int i = 0; i < n; i++) {
        cin >> time >> len;
        people.push(P(time, len));
    }
    cin >> k;
    double sum = 0;
    int maxWait = 0;
    while (!people.empty()) {
        P now = people.front();
        people.pop();
        int wait, id = getID(now.first, wait);
        sum += wait;
        maxWait = max(maxWait, wait);
        endtime[id] = now.first + now.second + wait;
    }
    int last = 0;
    for (int i = 1; i <= k; i++) {
        last = max(last, endtime[i]);
    }
    printf("%.1f", sum / (1.0 * n));
    cout << " " << maxWait << " " << last << endl;
}

6.六度空间（queue)

题目描述

六度空间理论指出：你和任何一个陌生人之间所间隔的人不会超过六个，也就是说，最多通过6个中间人你就能够认识任何一个陌生人。验证这一理论需要大数据量。现在，只需要计算任意两个人通过多少个中间人能互相认识。

假设有 n 个人，他们的编号为 1~n，其中有一些人相互认识，现在 x 想通过一些中间人认识 y（如果 a 认识 b，b 认识 c，那么 a 可以通过 b 来认识 c），编程求出 x 最少需要通过多少人才能认识 y。

思路：x入队列。只有队列非空，取队头元素，队头元素为y，结束。否则，访问队头元素所在的行，他认识的人还未入对，则入队。因还有通过多少人认识，入队除元素外，加层次。x层次为0。x认识的为1，再下一次为2。

该题是从x出发，一层层找他认识的人，直到找到y，或队列空，即找不到y。

输入

第一行，测试次数t

每组测试数据格式如下：

第 1 行 3 个整数 n、x、y，2≤n≤100；
接下来的 n 行是一个 n×n 的邻接矩阵，
a[i][j]=1 表示 i 认识 j，a[i][j]=0 表示不认识。
保证 i=j 时，a[i][j]=0，并且 a[i][j]=a[j][i]。

输出

每组测试数据，输出一行，输出x 认识 y 最少需要通过的人数。如果x通过中间的人不能认识y，输出no。

样例输入

2
5 1 5
0 1 0 0 0
1 0 1 1 0
0 1 0 1 0
0 1 1 0 1
0 0 0 1 0
5 4 5
0 1 0 1 0
1 0 1 0 0
0 1 0 0 1
1 0 0 0 0
0 0 1 0 0

样例输出

2
3

题解

#include<bits/stdc++.h>

using namespace std;
int n;
int mp[105][105], dis[105];

void bfs(int s) {
    dis[s] = 0;
    queue<int> q;
    q.push(s);
    while (q.size()) {
        int u = q.front();
        q.pop();
        for (int i = 1; i <= n; i++) {

            if (mp[u][i] && dis[i] == 0) {

                q.push(i);
                dis[i] = dis[u] + 1;

            }
        }
    }

}

int main() {
    int t, s, to;
    cin >> t;
    while (t--) {
        cin >> n >> s >> to;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                cin >> mp[i][j];
            }
            dis[i] = 0;
        }

        bfs(s);
        if (dis[to] == 0) cout << "no" << endl;
        else cout << dis[to] - 1 << endl;
    }
}

以上是关于面向对象程序设计（荣誉）实验四 deque,stack,queue的主要内容，如果未能解决你的问题，请参考以下文章

面向对象程序设计（荣誉）实验一 String

面向对象程序设计（荣誉）实验三算法及list

面向对象程序设计（荣誉）实验六 set,bitset,multimap

面向对象程序设计（荣誉）实验七 unordered_set

面向对象程序设计（荣誉）实验五 priority_queue,map

面向对象程序设计（荣誉）大作业

面向对象程序设计（荣誉）实验四 deque,stack,queue

目录

1.双向队列(deque)

题目描述

输入

输出

样例输入

样例输出

题解

2.括号匹配(stack)

题目描述

输入

输出

样例输入

样例输出

题解

3.田忌赛马(deque)

题目描述

输入

输出

样例输入

样例输出

题解

4.火车站(stack)

题目描述

输入

输出

样例输入

样例输出

题解

5.银行单队列多窗口模拟(queue)

题目描述

输入

输出

样例输入

样例输出

题解

6.六度空间（queue)

题目描述

输入

输出

样例输入

样例输出

题解