算法设计与分析实验一排序算法性能分析

Posted 2021-07-11 上山打老虎D

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了算法设计与分析实验一排序算法性能分析相关的知识，希望对你有一定的参考价值。

实验一排序算法性能分析

一、实验目的与要求
- 1、实验基本要求
- 2、实验亮点
二、实验内容与方法
三、实验步骤与过程
四、实验结论或体会
五、思考

一、实验目的与要求

1、实验基本要求

①掌握选择排序、冒泡排序、合并排序、快速排序、插入排序算法原理
②掌握不同排序算法时间效率的经验分析方法，验证理论分析与经验分析的一致性。

2、实验亮点

①除了基本五种排序算法，额外选择了基数排序，希尔排序和堆排序三种排序算法进行性能分析并对一些算法提出优化方案。
②使用Tableau进行绘图，完成数据可视化
③对实验过程中发现的相关问题进行了探究并解决
④分析了每一种情况下理论时间消耗与实际时间消耗偏差的原因。
⑤实现了对部分算法的优化以及思考题对一万亿数据的排序问题

二、实验内容与方法

排序问题要求我们按照升序排列给定列表中的数据项，目前为止，已有多种排序算法提出。本实验要求掌握选择排序、冒泡排序、合并排序、快速排序、插入排序算法原理，并进行代码实现。通过对大量样本的测试结果，统计不同排序算法的时间效率与输入规模的关系，通过经验分析方法，展示不同排序算法的时间复杂度，并与理论分析的基本运算次数做比较，验证理论分析结论的正确性。

三、实验步骤与过程

（一）独立算法性能分析

1. 冒泡排序

（1）算法实现原理
①比较相邻的元素。如果第一个比第二个大，就交换他们两个。
②对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
③针对所有的元素重复以上的步骤，除了最后一个。
④持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

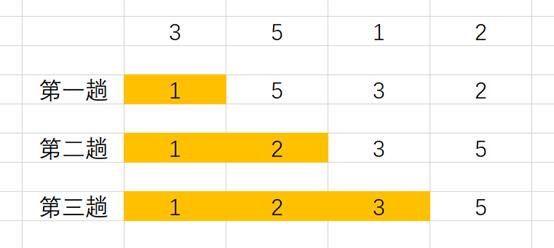
下面以使用冒泡排序3,5,1,2这四个数字为例，以图示介绍冒泡排序，见下图

在这里插入图片描述

（2）源代码

BUBBLESORT(A)
	for i = 1 to A.length-1
		for j = A.length downto i + 1
			if A[j] < A[j - 1]
				exchange A[j] with A[j - 1]

（3）算法性能分析：
①时间复杂度分析：
若文件的初始状态是正序的，一趟扫描即可完成排序。所需的关键字比较次数C和记录移动次数M均达到最小值

$C_{min}=n-1$

$M_{min}=0$

所以，冒泡排序最好的时间复杂度为 $O (n)$
若初始文件是反序的，需要进行n-1趟排序。每趟排序要进行n-i次关键字的比较 $(1 \leq i \leq n - 1)$ ，且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值：
$C_{max}=\\frac{n(n-1)}{2}=O(n^2 )$
$M_{max}=\\frac{3n(n-1)}{2}=O(n^2 )$

冒泡排序的最坏时间复杂度为 $O(n^2 )$
综上，因此冒泡排序总的平均时间复杂度为 $O(n^2 )$

②数据测试分析：
使用随机数生成器生成了从 $10^1$ 到 $10^6$ 的不同数据量级的随机数，通过使用冒泡排序进行排序并获取了程序运行时间。为降低偶然性，对20组数据取平均值，选择 $10^5$ 时运行时间为理论值并做表如下：

数据量级	平均时间(ms)	平均时间对数	理论值(ms)	理论值对数
$10^1$	0.000160	-3.795880017	0.000123	-3.9102255
$10^2$	0.006225	-2.205860644	0.0122963	-1.9102255
$10^3$	0.572565	-0.242175203	1.22963	0.08977445
$10^4$	102.0520	2.00882152	122.963	2.08977445
$10^5$	12296.30	4.08977445	12296.3	4.08977445
$10^6$	1236880	6.092327567	1229630	6.08977445

通过获得的数据，使用 $10^5$ 时的时间消耗为基准理论值，使用Tableau做图像并拟合如图：
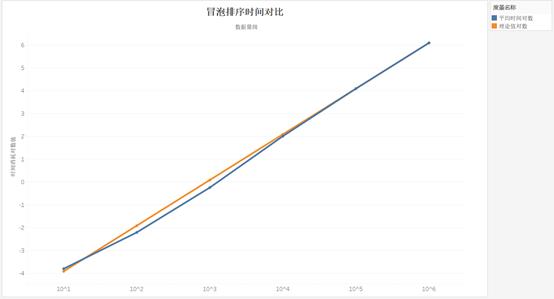
在这里插入图片描述
由于冒泡排序算法时间复杂度为 $O(n^2 )$ ，故，数量级扩大10倍时，时间消耗应扩大100倍。由上图，可得随着数据量的增大，拟合效果越好，所有实验数据符合 $O(n^2 )$ 的时间复杂度。
从上图可知，实际时间消耗曲线与理论时间消耗基本拟合，冒泡排序算法的时间复杂度满足 $O(n^2 )$ 。

2. 选择排序

（1）算法实现原理
①首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
②从剩余未排序元素中继续寻找最小（大）元素，放到已排序序列的末尾。
③重复上述过程直至所有元素均排序完毕。

下面以使用选择排序3,5,1,2这四个数字为例，以图示介绍选择排序，见下图
在这里插入图片描述

（2）源代码

SELECTSORT(ele)
	for i=0 to n-2
    min=i
    for j= i+1 to n-1
        if ele[min]>ele[j]  min=j
    swap(ele[i],ele[min])

（3）算法性能分析
①时间复杂度分析：
选择排序的交换操作介于 $0$ 与 $n - 1$ 次之间。选择排序的比较操作为 $n (n - 1) / 2$ 次之间。选择排序的赋值操作介于 $0$ 和 $3 (n - 1 ）$ 次之间。比较次数为 $O(n^2 )$ 。比较次数与关键字的初始状态无关，总的比较次数 $N = (n - 1) + (n - 2) + . . . + 1 = n (n - 1) / 2$ 。
交换次数 $O (n)$ ，最好情况是，已经有序，交换0次；最坏情况交换 $n - 1$ 次，逆序交换 $n / 2$ 次。因此选择排序的时间复杂度为 $O(n^2 )$

②数据测试分析：
使用随机数生成器生成了从 $10^1$ 到 $10^6$ 的不同数据量级的随机数，通过使用选择排序进行排序并获取了程序运行时间。为降低偶然性，对20组数据取平均值，选择 $10^5$ 时运行时间为理论值并做表如下：

数据量级	平均时间(ms)	平均时间对数	理论值(ms)	理论值对数
$10^1$	0.00011	-3.958607315	0.00002544	-4.5944829
$10^2$	0.003785	-2.421934116	0.002544	-2.5944829
$10^3$	0.325995	-0.486789061	0.2544	-0.5944829
$10^4$	29.286	1.466660058	25.544	1.40728891
$10^5$	2554.4	3.407288906	2554.4	3.40728891
$10^6$	257163	5.410208483	255440	5.40728891

通过获得的数据，使用 $10^5$ 时的时间消耗为基准理论值，使用Tableau做图像并拟合如图：
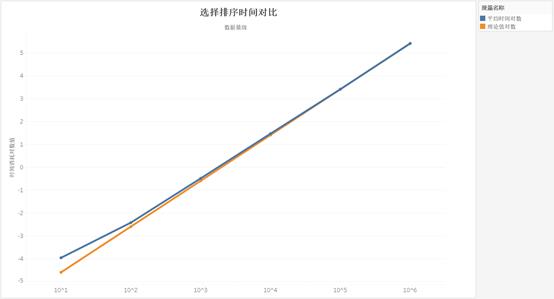
在这里插入图片描述
由于选择排序算法时间复杂度为 $O(n^2 )$ ，故，数量级扩大10倍时，时间消耗应扩大100倍。由上图，可得随着数据量的增大，拟合效果越好，所有实验数据符合 $O(n^2 )$ 的时间复杂度。
从上表和上图中可以发现整体时间消耗都大致满足数量级扩大10倍，时间消耗扩大100倍的规律。但对于 $10^1,10^2$ 数量级时存在较大误差，拟合效果较差。通过分析可知，选择排序中进行了很多次相互调换元素（相互赋值）的操作，从而造成了时间浪费。我进行了如下两次对比实验，使用库函数swap和手写调换元素的函数进行对比，可以发现，使用swap函数的小数据拟合效果要明显好于手写。因此，小数据下，较差的拟合效果是因为较多次交换占用了更多时间，当数据较小时，数据交换造成的时间损耗更明显。但当数据变多时，这种影响被冲淡，故拟合效果比较好。

3. 插入排序

（1）算法实现原理
①假设前面 $n - 1$ (其中 $n \geq 2$ )个数已经有序的，现将第n个数插到前面有序序列中，并找到合适位置，使得插入第 $n$ 个数后仍为有序序列
②按照此法对所有元素进行插入，直至整个序列为有序序列

（2）源代码

INSERTION-SORT(A)
    for j=2 to A.length:
        key=A[j]
        //将A[j]插入已排序序列A[1..j-1]
        i=j-1
        while i>0 and A[i]>key
            A[i+1]= A[i]
            i=i-1
        A[i+1]=key

下面以使用插入排序3,5,1,2这四个数字为例，以图示介绍插入排序，见下图
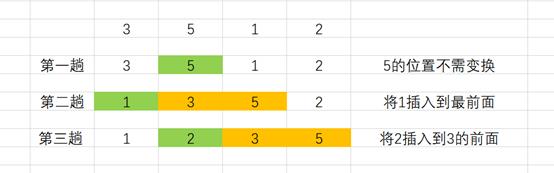
在这里插入图片描述