算法设计与分析 实验二 分治法求解最近点对问题

Posted 上山打老虎D

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了算法设计与分析 实验二 分治法求解最近点对问题相关的知识，希望对你有一定的参考价值。

分治法求解最近点对问题

一、实验目的与要求

1、实验基本要求

（1） 掌握分治法思想。
（2） 学会最近点对问题求解方法。

2、实验亮点

（1）通过暴力法以及分治法详细介绍“最近点对”问题的实现方法
（2）完成两种算法的图形界面可视化，使算法执行过程更清晰
（3）完成数据运行效率的对比
（4）自行绘制了算法示意图和算法流程图，实验展示更清晰
（5）完成了分治法在三维下的推广

二、实验内容与方法

  1. 对于平面上给定的N个点，给出所有点对的最短距离，即，输入是平面上的N个点，输出是N点中具有最短距离的两点。
  2. 要求随机生成N个点的平面坐标，应用蛮力法编程计算出所有点对的最短距离。
  3. 要求随机生成N个点的平面坐标，应用分治法编程计算出所有点对的最短距离。
  4. 分别对N=100,1000,10000,100000，统计算法运行时间，比较理论效率与实测效率的差异，同时对蛮力法和分治法的算法效率进行分析和比较。
  5. 如果能将算法执行过程利用图形界面输出，可获加分。

三、实验步骤与过程

（一）一些准备工作

1、实验流程

通过随机数生成器生成double型点集数据。然后对点对集合分别使用暴力穷举法与分治法进行运算，编程计算出所有点对的最短距离及运行时间，最后进行算法效率分析与对比得出实验结论。

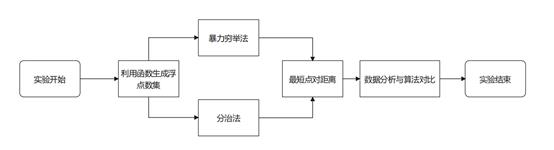
在这里插入图片描述

2、数据生成与去除重复点

可以通过C++自带函数生成随机值。但随机值生成过程中有可能存在生成重复点的情况，因此需要对重复的点进行剔除。
在此我使用unordered_set结构并利用哈希完成对重复点的剔除。
①首先定义点结构体：

//定义点结构体  

struct Point {
    double x, y;
};

②重载比较函数与哈希函数

//重载比较函数
struct eqfunc {
    bool operator()(const Point &p1, const Point &p2) const {
        return ((p1.x == p2.x) && (p1.y == p2.y));
    }
};
	  
//重载哈希函数
struct hashfunc {
    size_t operator()(const Point &P) const {
        return size_t(P.x * 201928 + P.y);
    }
};

③使用函数生成数据并利用哈希对重复点进行剔除

//利用哈希函数进行去重
unordered_set<Point, hashfunc, eqfunc> hash;
//遍历赋值并哈希去重
for (int i = 0; i < length; i++) {
	point[i].x = dist(eng);
	point[i].y = dist(eng);
	if (hash.find(point[i]) == hash.end()) 	{
		hash.insert(point[i]);
		}else {
          i--;
        }
}

对于每个生成的随机数，分别赋值给横纵坐标，再利用哈希函数，如果在集合中找不到，则说明点未重复，则进行下一个点的生成。如果找到点，则将计数器自减1，并重新生成该点的横纵坐标值。

（二）暴力穷举法

1、算法描述

暴力穷举法即遍历求出每个点之间的距离，并选择距离最小的点进行输出。
具体流程图如下：
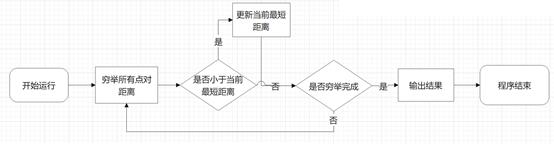
在这里插入图片描述

2、时间复杂度分析

不妨将问题看成一个求n边无向完全图的问题。则对于 n n n个顶点有每个顶点存在连边 n − 1 n-1 n−1条，又因为是无向图，则共有连边 C = n ( n − 1 ) 2 C=\\frac{n\\left(n-1\\right)}{2} C=2n(n−1)​。因此时间复杂度为 O ( n 2 ) O\\left(n^2\\right) O(n2)

3、编程实现

double ans = INF; //设定初始结果为无穷大
for (int i = 0; i <= length - 1; i++)
{
    for (int j = i + 1; j <= length - 1; j++)
    {
        //遍历每一组可能，并选择最小值存入结果
        ans = min(ans, dis(point[i], point[j]));
    }
}

设置初始结果为INF。通过外层的循环遍历各点，再内层的循环遍历还未与当前点比较过的点，当发现存在两点间距离小于目前结果时，则更新结果值为更小的距离，依次循环穷举所有点对间距离。

（三）分治法

1、算法描述

基于暴力穷举法，我们在实际运算中不难发现，存在一些“显然距离很远”的点对，对这些点对的距离运算并进行比较常常是一种无用功，将造成时间空间的双重浪费。因此能否找到一种方法精简暴力穷举法，降低无用比较次数呢？
与排序算法类似，完成实验一后，不难发现：对于排序算法，快速排序与归并排序与其余三个排序算法比都是比较省时间的。这说明，将一个大整体分为几个小部分进行“分而治之”是解决类似问题的好方法。因此，相似地，我们可以使用分治法，利用“分而治之”的思想对问题实现简化。依据分治法，我们可以设计出如下算法：
①对所有点按照其横坐标进行排序；
②若 n = 1 n=1 n=1，返回无穷大；
n = 2 n=2 n=2，计算距离并返回；
n > 2 n>2 n>2，以该组数组下标中值分割，即mid=(l+r)/2,mid_x=point[mid].x，将规模为n的问题分解为两个规模为 n 2 \\frac{n}{2} 2n​的子问题并重复步骤②，直到得到两个子问题的解 mindis1,mindis2；
③合并子问题的点并将其按y坐标排序；
④设mindis为两个子问题解中的较小值，遍历当前规模下所有点，找出横坐标范围在[mid_x-mindis,mid_x+mindis]的所有点；
⑤将步骤④中的所有点与按y坐标排好序后的其后6个基准点（具体算法证明将在下面完成）进行比较，如果距离小于 mindis 则更新 mindis 的值。

具体流程图如下：
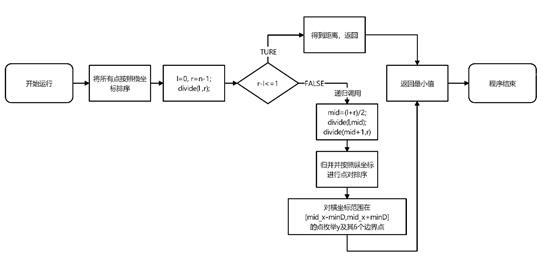
在这里插入图片描述

2、算法解释与正确性分析

（1）点集分块：
我们不妨将平面分为两个大致相等的点集再对问题进行考虑。
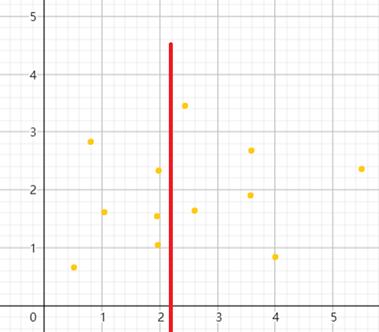
在这里插入图片描述
将平面的点分为两个点集，此时对于某点对中两个点p_1,p_2存在如下三种情况：
① p 1 , p 2 p_1,p_2 p1​,p2​都位于左侧点集
② p 1 , p 2 p_1,p_2 p1​,p2​都位于右侧点集
③ p 1 , p 2 p_1,p_2 p1​,p2​一个位于左侧点集，另一个位于右侧点集
对于情况①与②，可以通过递归进行解决，难点在于如何处理两个点不处于同一个点集的情况。

（2）鸽笼查找
不妨设左右两侧点集的最小距离为 d l d_l dl​, d r d_r dr​。因此有如下结论：

左、右侧点集中每个点对间距离均分别大于等于 d l d_l dl​, d r d_r dr​
因此，仅需对下图中蓝色方框内的异侧点对进行检测即可：

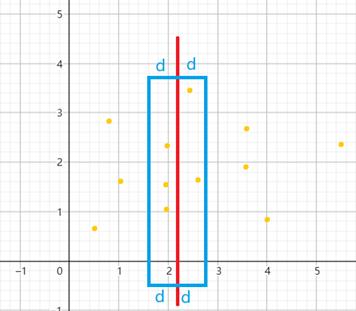
其中， d = min ⁡ ( d l , d r ) d=\\min{\\left(d_l,d_r\\right)} d=min(dl​,dr​)。
对于蓝色区域内的点，如果仍然采用暴力穷举法对每个点对进行检测，不能实质性降低时间复杂度以节省时间。因此，我们可以利用鸽笼原理，找到对应的基准点进行检测。
如下图，当对 [ l − δ , l + δ ] \\left[l-\\delta,l+\\delta\\right] [l−δ,l+δ]中的点进行归并后，这些点在数组中关于y坐标已经有序，不妨设最终情况为 p L , p R p_L,p_R pL​,pR​两点分别位于点集 P L , P R P_L,P_R PL​,PR​，且该点对间距离小于 δ \\delta δ，则 p L , p R p_L,p_R pL​,pR​两点一定位于下图中 2 δ × δ 2\\delta\\times\\delta 2δ×δ的浅绿色矩形内。这是因为根据分析，当且仅当点对位于该浅绿色区域内时，两点间纵坐标之差小于 δ \\delta δ，任何其他不在该范围内的点横坐标或纵坐标之差必定大于 δ \\delta δ，距离必定大于 δ \\delta δ，此时，该点对间距离一定不为最小，故无需进行比较。
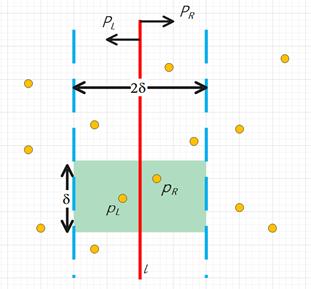
在这里插入图片描述
此时，对于下图中矩形左半边的 δ × δ \\delta\\times\\delta δ×δ正方形，因为 P L P_L PL​中所有点之间最小距离为 δ \\delta δ，依鸽笼原理，该正方形内最多有4个点（如下图）。类似地，P_R中也最多有4个点可以位于该 δ × δ \\delta\\times\\delta δ×δ正方形内。又因为两个正方形存在一条边完全重合，故有两个点为同一个点，因此在判断时只需判断每个点与其余6个基准点间距离关系即可。

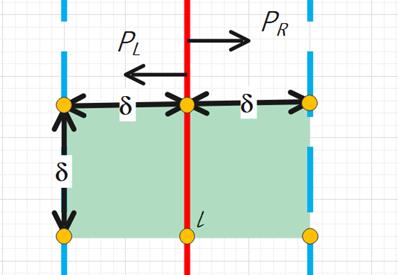
在这里插入图片描述

（3）点集排序

对于算法中③合并子问题时，需要对点进行按照纵坐标的排序，此时不应直接在递归调用中使用排序算法进行排序。否则时间递归式将变为 T ( n ) = 2 × T ( n 2 ) + O ( n log ⁡ n ) T\\left(n\\right)=2\\times T\\left(\\frac{n}{2}\\right)+O\\left(n\\log{n}\\right) T(n)=2×T(2n​)+O(nlogn)，最终时间复杂度将变为 O ( n log ⁡ 2 n ) O\\left(n\\log^2{n}\\right) O(nlog2n)。因此需要使用类似归并排序的思路，即将已经排序的数组 Y l Y_l Yl​和 Y r Y_r Yr​进行合并形成有序数组。

3、时间复杂度分析

①使用了归并方法后对纵坐标的排序在递归过程中的每一层都为线性效率，在具体算法实现中对每次递归中按照纵坐标的排序与归并排序中合并操作十分类似。即按照纵坐标将有序数组 Y L , Y R Y_L,Y_R YL​,YR​进行合并从而形成有序数组Y。这是由于分治函数中当递归至仅有两个点时将直接合并并向上返回，因此，返回时待合并的两个数组 Y L , Y R Y_L,Y_R YL​,YR​是有小规模合并而来，因此 Y L , Y R Y_L,Y_R YL​,YR​一定是纵坐标有序的，继续合并后的数组也为纵坐标有序的数组，这样保证了每次操作一定范围内的点集时，点集内点都已经为纵坐标有序
通过分析算法，易得每次合并操作中比较的交换次数满足如下式子
1 2 ( r i g h

以上是关于算法设计与分析 实验二 分治法求解最近点对问题的主要内容，如果未能解决你的问题，请参考以下文章

分治法二（平面最近点对）

算法分析与设计实验报告 Project5

前端面试 ——“算法设计与分析”

算法设计与分析 实验四 动态规划求解流水线问题

分治&暴力求解最近点对问题 + 时间性能量化分析

算法设计与分析知识点整理