算法设计与分析实验六最大流解决论文评审问题

Posted 2021-07-11 上山打老虎D

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了算法设计与分析实验六最大流解决论文评审问题相关的知识，希望对你有一定的参考价值。

一、实验目的与要求

1、实验目的：

（1）掌握最大流算法思想。
（2）学会用最大流算法求解应用问题。

2、实验亮点：

（1）正确构建了流网络，并详细分析了流网络的结果
（2）给出了流网络与问题解的关系
（3）使用多种方法正确计算了给定网络的最大流
（4）对多种算法实现过程中必要定理进行了严谨的证明

二、实验内容与方法

使用最大流解决论文评审问题：
（1）有m篇论文和n个评审，每篇论文需要安排a个评审，每个评审最多评b篇论文。请设计一个论文分配方案。
（2）要求应用最大流解决上述问题，画出m=10，n=3的流网络图并解释说明流网络图与论文评审问题的关系。
（3）编程实现所设计算法，计算a和b取不同值情况下的分配方案，如果没有可行方案则输出无解。

三、实验步骤与过程

（一）设计流网络

要想利用网络流解决问题，第一步当然是构建流网络。为了让流网络结构更加清晰，我采用了层次的概念对流网络进行构建。下图为构建出的网络流结果，其中，省略了一些重复的节点。
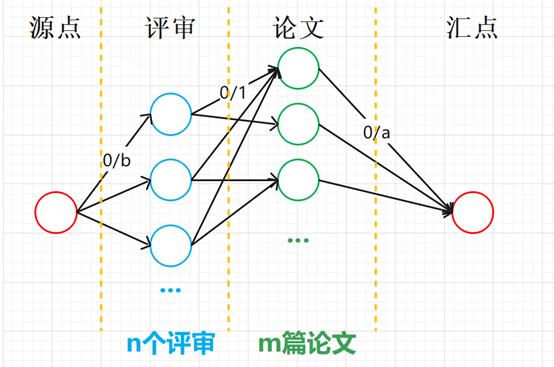
在这里插入图片描述

根据题意，可以构建出如上流网络。其中，流网络共分四层。第一层只有源点，第四层只有汇点。中间第二层表示各个评审，第三层表示各个待评审的论文。
源点→评审： 源点分别指向各个评审节点且容量都为每个评审的最大评审论文数。由于需要对各个论文进行评审，所以源点与每个评审间存在有向边。又因为每个评审最多可以评审b篇论文，因此，从源点到评审节点的最大流量为b。

评审→论文： 对于每个已经分配的评审，评审需要评阅论文，因此存在由评审到论文的有向边。又因为对于每个评审，其评阅论文的状态只有0或1即表示未评阅或已评阅。因此从评审到论文的有向边的最大流量为1。

论文→汇点： 完成论文的评阅后将流网络汇入汇点即可。又因为，每个论文至少由a名评审进行评阅，则从论文节点到汇点有最大容量为a的有向边。当 $doc_1$ 到汇点的容量为x时，表示论文 $doc_1$ 被x个评审评阅了。

下面以 $m = 10, n = 3$ （10篇论文，3位评审）时构建流网络为例，展示构建的完整流网络：
在这里插入图片描述
网络流说明与上方说明相同，此处不赘述。

（二）流网络中最大流与论文评审问题解的关系

首先，我们知道，流网络最大流下各边的流量就是一组值班问题的解：

当流网络流入汇点总量不为论文数与每篇论文需要评审数的积（m×a）时，说明有部分论文没有被规定数量（a）的评审评阅，此次论文评审问题无解；
当流网络流入汇点总量为论文数与每篇论文需要评审数的积（m×a）时，最大流为论文数与每篇论文需要评审数的积（m×a），此次论文评审问题有解。
此时关键路径【评审→论文】中某条边的流量不为 0，说明这条边被选中，即出发点评审对终点论文进行了评阅。

第一层与第二层之间的最大容量保证了每位评审的最大论文评阅数，第二层与第三层间的边表示了评审与论文的关系，即是否评阅。第三层与汇点间的最大容量限制表示了每个论文需要评审的数量。

显然，如果这个问题有解，即每篇论文都有a位评审进行评阅，那么从论文层到汇点间边的流量必为最大容量限制a。此时，最后一层与第一层间所有路径容量必全部流满，则此时流网络必为最大流，即论文评审问题的解一定对应流网络中的最大流情况。且论文评审问题是否有解的依据是最大流是否大于论文数与每篇论文需要评审数的积（m×a）。

（三）最大流的计算

经过上述流网络的分析与构建，论文评审问题已经转化为求给定流网络的最大流问题。对于最大流的求解有很多种方式，本次实验将介绍Edmonds-Karp 算法改进后的 Dinic 算法。
接下来，将介绍 Edmonds-Karp 算法以及该算法涉及的关键定理，并介绍 Dinic 算法以及具体的Dinic 算法的实现方法。

1、Edmonds-Karp 算法

（1）算法思想：

因为所有流量都将从源点 s 出发，经过中间点后最终汇至汇点 t。因此最大流的网络可以拆分成一系列增广路的集合。其中，每条增广路的流量就是当前增广路上所有边的容量限制的最小值。因此可以通过不断搜索增广路径，并消去增广过程中产生的这条增广路径所消耗的流量，并不断更新流量完成最大流问题的求解。
在这里插入图片描述
由于增广路的搜索需要一定的顺序，不同的顺序会导致不同的结果。因此可能会因为搜索顺序不合适导致最大流求解错误。因此，可以引入残留网络，完成对错误搜索增广路产生的流量退回。
在残留网络中对每一条边增加一条反向边，其容量与原边相同，流量为原边最大限制容量与原边已使用流量之差。
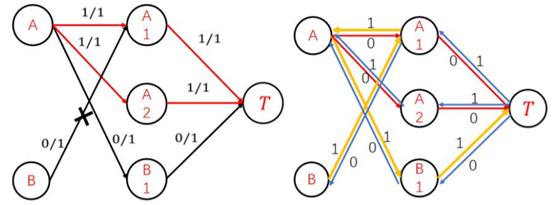
在这里插入图片描述
如上图，不引入残留网络时可能先找到两条通路 $(A, A 1, T)$ 与 $(A, A 2, T)$ ，这将导致流经后面 B1 时已经流量满，而无法连接节点造成最大流求解错误。引入残留网络后就可以将 $(A, A 1, T)$ 这条通路给 B，最终将得到正确的最大流结果。

（2）算法关键定理及其证明：

①增广路定理：
残留网络中任何一条从 s 到 t 的有向通路都对应原图中一条增广路。只需求解出该道路中所有残量的最小值 $d_{min}$ ，并把所有对应边流量增加 $d_{min}$ 即可，这个过程被称为增广。显然，网络流中的流量可以增大，当且仅当当前网络中存在增广路。因此当残留网络中不存在增广路，则当前流即为最大流。这就是著名的增广路定理，它介绍了增广路解决最大流的思路，Edmonds-Karp算法和 Dinic 算法都是基于增广路方法的具体实现。

②证明增广路径长度递增：
不妨设 $p$ 为第一次 BFS找到的增广路，则 $p$ 必为残留网络 $(s, t)$ 中最短路径。在进行增广后， $p$ 上关键边 $(u, v)$ 将在残留网络中删去并增加反向边 $(v, u)$ 。设第一次找到的增广路径是 $p = (s \to u \to v \to t)$ ，关键边为 $(u, v)$ 。此时进行增广操作后，将从残留网络中删去正向边 $(u, v)$ ，并增加反向边 $(v, u)$ 。
为了证明增广路径长度递增，我们不妨假设下一次 BFS 搜索出现了长度更短的路径 $p^{'}$ ，则一定出现反向边 $(v, u) ， p^{'} = (s \to v \to u \to t)$ 。而 BFS 性质保证第一次搜索中 $d i s (s, u)$ 与 $d i s (v, t)$ 都是最短的，此时有
$d i s (s, t) = d i s (s, u) + d i s (v, t) + 1$
若出现了更短的边，则有
$∣ p^{'} ∣ = d i s^{'} (s, v) + d i s^{'} (u, t) + 1 < ∣ p ∣$
而
$d i s (s, v) \leq d i s^{'} (s, v), d i s (u, t) \leq d i s^{'} (u, t)$
与假设矛盾，因此不存在长度更短的路径 $p^{'}$ ，即BFS 找到的增广路径长度是递增的。
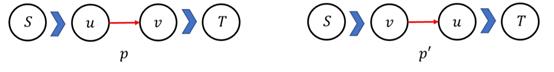
在这里插入图片描述
③证明Edmonds-Karp算法迭代具有有穷上界
对于任一残留网络，在沿任一条增广路径增加流后，处于该条路径上所有关键边都将从残留网络中消失。并且任意一条增广路上都至少存在一条关键边。
因此，只需证明对于|E|中的每条边来说，其成为关键边的次数是有穷的并且为定值。此处先给出结论如下：
$∣ E ∣$ 中的每条边成为关键边的次数最多为 $\\frac{|V|}{2}$ 次

接下来给出证明：
不妨设 u 和 v 为集合 V 中的两个节点，且这两个节点由 E 中的一条有向边连通。由于增广路径都是最短路径，因此当边 $(u, v)$ 第一次成为关键边时，此时有：
$δ_f (s,v)=δ_f (s,u)+1$
在对流进行增加后，边 $(u, v)$ 将被从残留网络中删除。并且，以后也不会重新出现，在另一条增广路径上，直到从 $u$ 到 $v$ 的网络流减小后为止，并且只有当 $(u, v)$ 出现在增广路径上时，这种情况才会发生。如果当这一事件发生时 $f^{'}$ 是 $G$ 的流，则有
$δ_f' (s,u)=δ_f' (s,v)+1$
依②中证明，有：
$δ_f (s,v)≤δ_f' (s,v)$
联立得：
$δ_f' (s,u)=δ_f' (s,v)+1≥δ_f (s,v)+1=δ_f (s,u)+2$