Lenet实现mnist数据集分类

Posted 2021-07-11 ZHW_AI课题组

目录

• 1.作者介绍
• 2.MINST数据集的介绍
• 3.LeNet网络结构
• • 输入层
  • C1层
  • S2层
  • C3层
  • S4层
  • C5层
  • F6和输出层
• 4.结果输出及损失函数的解释
• • 损失函数
  • 结果展示
• 5.LeNet代码附详细注解

1.作者介绍

陈锡伟,男，西安工程大学电子信息学院，2020级硕士研究生，张宏伟人工智能课题组。
研究方向：机器视觉与人工智能
电子邮件：[e-mail]

2.MINST数据集的介绍

MINST数据集是手写0到9组成的数据集，来自 250 个不同人手写的数字构成，分为六万张训练集和1万张测试集，包含以下四个文件：
Training set images: train-images-idx3-ubyte.gz (9.9 MB, 解压后 47 MB, 包含 60,000 个样本)
Training set labels: train-labels-idx1-ubyte.gz (29 KB, 解压后 60 KB, 包含 60,000 个标签)
Test set images: t10k-images-idx3-ubyte.gz (1.6 MB, 解压后 7.8 MB, 包含 10,000 个样本)
Test set labels: t10k-labels-idx1-ubyte.gz (5KB, 解压后 10 KB, 包含 10,000 个标签)
也就是一个标签对应一张图，这样方便计算机确认自己识别的是否是对的

3.LeNet网络结构

LeNet-5是一个较简单的卷积神经网络包含了深度学习的基本模块：卷积层，池化层，全连接层下图就是网络的基本流程图，接下来我们将逐层分析

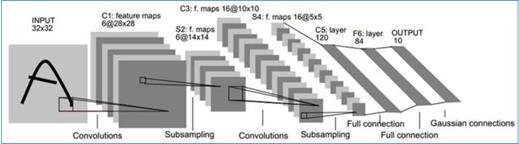
输入层

首先是输入层INPUT,输入32*32大小的原始图像

C1层

接下来是C1层，第一个卷积层。卷积层的目的就是为了获取图像特征，获取 的方式就是通过卷积核实现。比如说，曲线卷积核就可以提取曲线这一图像特征。C1使用的卷积核大小是55，一共有六个卷积核，步长（卷积核扫过图片前一次与后一次相隔的距离）为1。
下图就是卷积的工作原理原图66，卷积核3*3，图中就是正在进行卷积，Kernel就是卷积核，紫色是图片该部分与卷积核进行卷积运算，结果就是第三张图蓝色的部分。第三张图就是我们获得的特征图。

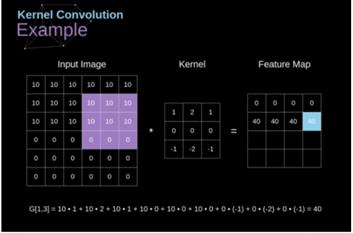
使用六种卷积核分别与原图进行卷积后就会获得六个大小为28*28的特征图，也就是我们C1显示的图像

S2层

下一个是S2,池化层。池化大小是22，步长为2。池化层的目的是减少计算参数，因为我们目前获得的特征图是六层的2828的，所包含的参数数量是十分庞大的，这就需要我们减少参数，池化层的作用就是这个。如何压缩呢，目前池化有两种，一种是通过选择框的数据求和再取平均值然后在乘上一个权值和加上一个偏置值，组成一个新的图片，另一种是取四个数中的最大值。。如下图4x4的图片经过采样后还剩2x2，直接压缩了4倍。本层具有激活函数，为sigmod函数，而卷积层没有激活函数。同时池化层也不含卷积核

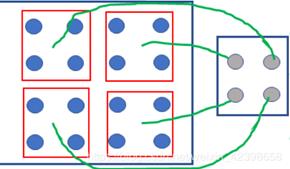
池化完成后就会获得如S2所示的14*14的六层特征图

C3层

C3层同样是卷积层，卷积核大小为5*5，个数为16但是这一步的卷积方式跟前面有所不同，这一层的卷积核为16个且并不是全连接而是部分连接，有些是C3连接到S2三层、有些四层、甚至达到6层，通过这种方式提取更多特征，下表就是这16个卷积核与S2层的六个特征图结合的方式

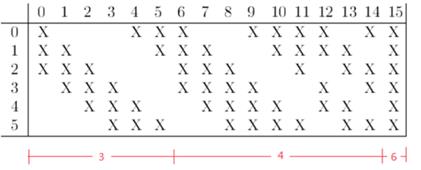
比如表格第一列代表的就是16个卷积核中的第一个卷积核，它是与S2六层特征图中的1，2，3三层进行卷积，然后将卷积的结果相加求和，再加上一个偏置，再取sigmoid得出卷积后对应的特征图，也就是C3的第一个特征图。其它列也是类似（有些是3个卷积模板，有些是4个，有些是6个）总共16个特征图。

S4层

S4与S2在结构核作用上一致，同样是池化作用，池化大小为22，个数为16。不再赘述，生成16个55的特征图

C5层

C5全连接层，大小为120。我们都知道图片是一个二维的数组，而全连接层就是要将他们降成一维的数组。方法同样是使用卷积。比如我们全连接前一层的特征图大小是55的，那么我们同样用55大小的卷积核扫过图像就可以只得到一个数，那么使用120个大小为55的卷积核就可以得到我们的C5层，120的一维数组。

F6和输出层

F6和输出层：全连接层中数组的每个数都代表着用于分类的最基本特征，比如有耳朵，有尾巴，有眼睛…（只是比如）最后再经过一个分类器（也是一个全连接层）,假设要分猫，狗，兔子，那么对这些特征再进行一次计算，将其中的某几个特征求和，输出最后的10的矩阵（输出层的10），每个数代表了各个类别的概率（或得分），本次项目代表的就是数字0到9的概率，采用的是径向基函数RBF来计算概率，也就是下图一。F6层中之所以大小是84的原因就是出于输出层的设计。计算机ASC码值的字符图，也就是下图二每一个都对应一个712的比特图，也就是84大小。而我们的数字0到9也在内这样方便我们对每一个像素点进行估计，确定输出的是哪一个。

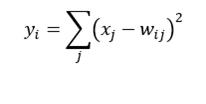
4.结果输出及损失函数的解释

损失函数

损失函数，就是用来估量你模型的预测值f(x)与真实值Y的不一致程度，它是一个非负实值函数,通常使用L(Y, f(x))来表示，损失函数越小，模型的鲁棒性（内部稳定性）就越好。

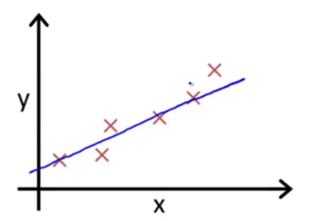
比如上面这张图，直线就是我们的预测值，而叉叉就是真实值，他们两的差值就是误差，我们自然是希望误差变小的，所以定义损失函数（用来表现预测与实际数据的差距程度）

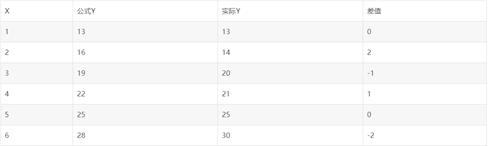
总差距程度，用公式Y-实际Y的绝对值：2+1+1+2+0+0=6为后续数学计算方便，我们通常使用平方损失函数代替绝对损失函数，将绝对值改为平方。那么可以看到，当总差距程度越小时我们的结果越准确，也就是为什么希望损失函数小。

结果展示

所以我们在训练的时候可以通过损失函数来判断我们模型的精确程度，同时来调节我们的内部参数，最终在训练完成后达到高识别度。
我们在使用MINST训练集训练完成模型后，就可以使用测试集进行测试了，将测试集图片输入模型，模型自己判断输入的图片对应哪一个数字，然后跟图片的标签进行对比来判断是不是正确的。准确率就是这么来的

5.LeNet代码附详细注解

这里要连接网络下载数据集，可能会很慢，如果报错请重新下载

import torch
import torchvision as tv
import torchvision.transforms as transforms
import torch.nn as nn
import torch.optim as optim
import argparse
# 定义是否使用GPU
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
torch.backends.cudnn.enabled = False
# 定义网络结构，只是定义，没有运行顺序
class LeNet(nn.Module):
    def __init__(self):
        super(LeNet, self).__init__()
        #构造网络有两种方式一个是seqential还有一个是module,前者在后者中也可以使用，这里使用的是sequential方式，将网络结构按顺序添加即可
        self.conv1 = nn.Sequential(     #input_size=(1*28*28)
            #第一个卷积层，输入通道为1，输出通道为6，卷积核大小为5，步长为1，填充为2保证输入输出尺寸相同
            nn.Conv2d(1, 6, 5, 1, 2), #padding=2保证输入输出尺寸相同
            #激活函数,两个网络层之间加入，引入非线性

            nn.ReLU(),      #input_size=(6*28*28)
            #池化层，大小为2步长为2
            nn.MaxPool2d(kernel_size=2, stride=2),#output_size=(6*14*14)
        )
        self.conv2 = nn.Sequential(
            nn.Conv2d(6, 16, 5),
            nn.ReLU(),      #input_size=(16*10*10)
            nn.MaxPool2d(2, 2)  #output_size=(16*5*5)
        )
        #全连接层，输入是16*5*5特征图，神经元数目120
        self.fc1 = nn.Sequential(
            nn.Linear(16 * 5 * 5, 120),
            nn.ReLU()
        )
        #全连接层神经元数目输入为上一层的120，输出为84
        self.fc2 = nn.Sequential(
            nn.Linear(120, 84),
            nn.ReLU()
        )
        #最后一层全连接层神经元数目10，与上一个全连接层同理
        self.fc3 = nn.Linear(84, 10)

    # 定义前向传播过程，输入为x，也就是把前面定义的网络结构赋予了一个运行顺序
    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        # nn.Linear()的输入输出都是维度为一的值，所以要把多维度的tensor展平成一维
        x = x.view(x.size()[0], -1)
        x = self.fc1(x)
        x = self.fc2(x)
        x = self.fc3(x)
        return x
#使得我们能够手动输入命令行参数，就是让风格变得和Linux命令行差不多
parser = argparse.ArgumentParser()
parser.add_argument('--outf', default='./model/', help='folder to output images and model checkpoints') #模型保存路径
parser.add_argument('--net', default='./model/net.pth', help="path to netG (to continue training)")  #模型加载路径
opt = parser.parse_args()

# 超参数设置
EPOCH = 8   #遍历数据集次数
BATCH_SIZE = 64      #批处理尺寸(batch_size)一次训练的样本数，相当于一次将64张图送入
LR = 0.001        #学习率

# 定义数据预处理方式，将图片转换成张量的形式,因为后续的操作都是以张量形式进行的
transform = transforms.ToTensor()

#下载四个数据集
# 定义训练数据集
trainset = tv.datasets.MNIST(
    root='./data/',
    train=True,
    download=False,
    transform=transform)

# 定义训练批处理数据
trainloader = torch.utils.data.DataLoader(
    trainset,
    batch_size=BATCH_SIZE,
    shuffle=True,
    )

# 定义测试数据集
testset = tv.datasets.MNIST(
    root='./data/',
    train=False,
    download=True,
    transform=transform)

# 定义测试批处理数据
testloader = torch.utils.data.DataLoader(
    testset,
    batch_size=BATCH_SIZE,
    shuffle=False,
    )

# 定义损失函数loss function 和优化方式（采用SGD）
net = LeNet().to(device)
criterion = nn.CrossEntropyLoss()  # 交叉熵损失函数，通常用于多分类问题上
optimizer = optim.SGD(net.parameters(), lr=LR, momentum=0.9) #梯度下降法求损失函数最小值

# 训练
if __name__ == "__main__":
      #八次遍历训练
    for epoch in range(EPOCH):
        sum_loss = 0.0
        # 读取下载的数据集
        for i, data in enumerate(trainloader):
            inputs, labels = data
            inputs, labels = inputs.to(device), labels.to(device)

            # 梯度清零
            optimizer.zero_grad()

            # forward + backward正向传播以及反向传播更新网络参数
            outputs = net(inputs)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()

            # 每训练100个batch打印一次平均loss，基本上是一直减小的，一个epoch有9个因为是6w张，一次batch64个
            sum_loss += loss.item()
            if i % 100 == 99:
                print('[%d, %d] loss: %.03f'
                      % (epoch + 1, i + 1, sum_loss / 100))
                sum_loss = 0.0
        # 每跑完一次epoch测试一下准确率
        with torch.no_grad():
            correct = 0
            total = 0
            for data in testloader:
                images, labels = data
                images, labels = images.to(device), labels.to(device)
                outputs = net(images)
                # 取得分最高的那个类
                _, predicted = torch.max(outputs.data, 1)
                total += labels.size(0)
                correct += (predicted == labels).sum()
            print('第%d个epoch的识别准确率为：%d%%' % (epoch + 1, (100 * correct / total)))
    #torch.save(net.state_dict(), '%s/net_%03d.pth' % (opt.outf, epoch + 1))