排序的那些事

Posted 2021-07-09 Jack Chao

排序的那些事（一）

排序可以说事计算机算法入门的一件事情。各种各样的排序，有的好有的差。
那让我们来看看这些排序的各种魅力吧。

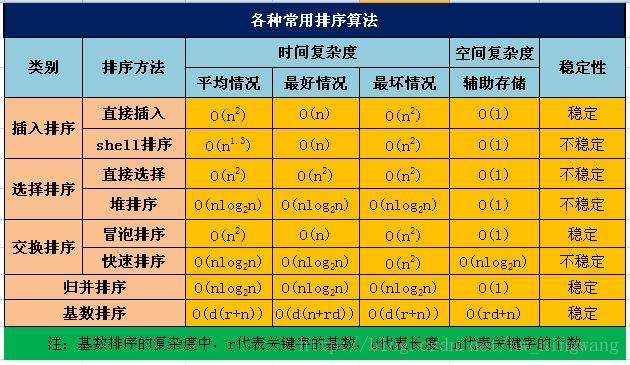
这张图片是我从网上借鉴过来的。这张图片很好的介绍了所有的基本排序。

直接插入排序

直接插入排序是一种最简单的排序方法，它的基本操作是将一个记录插入到已经排好序的有序表中，从而得到一个新的记录增加1的有序表。也就是选一个放一个。这个的时间复杂都市O（n^2）;
但是当我学到后面可以发现，这个O(n^2)比冒泡和选择的要快一点。
话不多说先上代码：

void InsortSort(int* a, int n) //插入排序  a 是数组 ， n是数组的大小
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;                   //定义一个变量指向排好数组的最后一个变量。
		int temp = a[end + 1];       // 定义一个变量，这个变量是排好数组的后面一个变量。用来插入到有序数组的变量。
		while (end >= 0)    //这个循环就是整个排序最重要的地方。整个循环就是让我们的还没排序的变量找到自己应该在的地方。
		{
			if (a[end] > temp)  //这边采用的是升序，如果想降序就可以改变这里。
			{
				a[end + 1] = a[end];     //如果没排序的值小于已经排序好数组的最后一个，那么就让排好序的最后一个数字放到后面，让出自己的位置。
				end--;    //end--是为了跟前面的数字依次比较。
			}
			else
			{
				break;
			}
		}
		a[end + 1] = temp;     //将没排序的放到应该在的位置。然后循环继续，将排好序的数组不断扩大。
	}
}

关于直接插入排序的解释大都放到代码那边了。相信文字的力量还是没办法让你理解。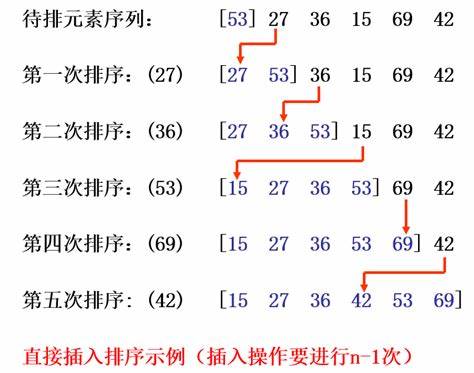

希尔插入排序

希尔排序是对直接插入排序的优化。我们知道，前面这个直接插入排序是一个个比较的。而插入 排序对于接近顺序的数组排序是很快的。那么，希尔就找到了这个突破口。在一个个排序之前先进行预处理。
话不多说，先看代码

//希尔排序，是对直接插入排序的优化
//第一步：预处理，让数组接近有序
//第二步：进行插入排序
void ShellSort(int* a, int n)
{
	int gap = n;    //先定义一个变量，来方便预处理。
	while(gap>1)
	{
		gap /= 2;  //在习惯上，我们会每次缩小两倍来改变变量
		for (int i = 0; i < n - gap; i++)  //这边循环的解释同直接插入排序
		{
			int end = i; 
			int temp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > temp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = temp;
		}
	}
}

我们可以看到大部分的代码和直接插入差不多。那么这个希尔排序是怎么实现的呢？
看图：

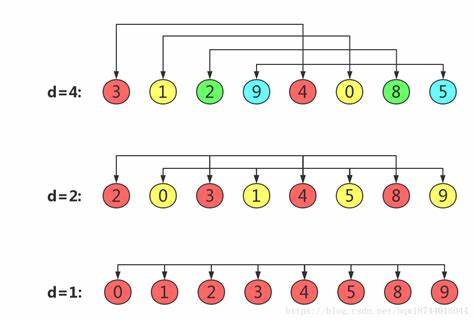
这边的d就是代码里面的gap；希尔排序就是多次的直接插入排序。
如果我们按照普通思维，我们会发现，希尔排序的时间花费好像比直接插入排序高，其实不然。希尔排序的时间复杂度是O(log2n)；其实希尔排序还有其他的变形，这边只是带大家了解一下，之后会出，关于这些排序代码的详细代码。

选择排序

这个应该是最容易理解的一个排序了。就是从一大堆的数字中找到最大（最小）然后把他们放到最开始或最后面，实现逆序或者顺序。
话不多说，先看代码：

void selectSort(int* a, int n)
{
	int t = 0;  //用于交换的变量
	int i = 0;  //控制趟数的变量
	int j = 0;  //用于元素之间比较的代码
	int flag = 0; //用于标记最大值的下标
	for (i = 0; i < n-1; i++)
	{
		int max = a[i];   //假定一个最大值
		for (j = i+1; j < n; j++)
		{
			if (max < a[j])
			{
				max = a[j];     //如果最大值不是max就改变
				flag = j;
			}
		}
		if (max != a[i])
		{
			t = a[i];
			a[i] = a[flag];   //如果最大值和最开始的值不一样了就交换
			a[flag] = t;
		}
	}
}

这个代码相信大家都有了解，不过我还是找了图给大家加深了解

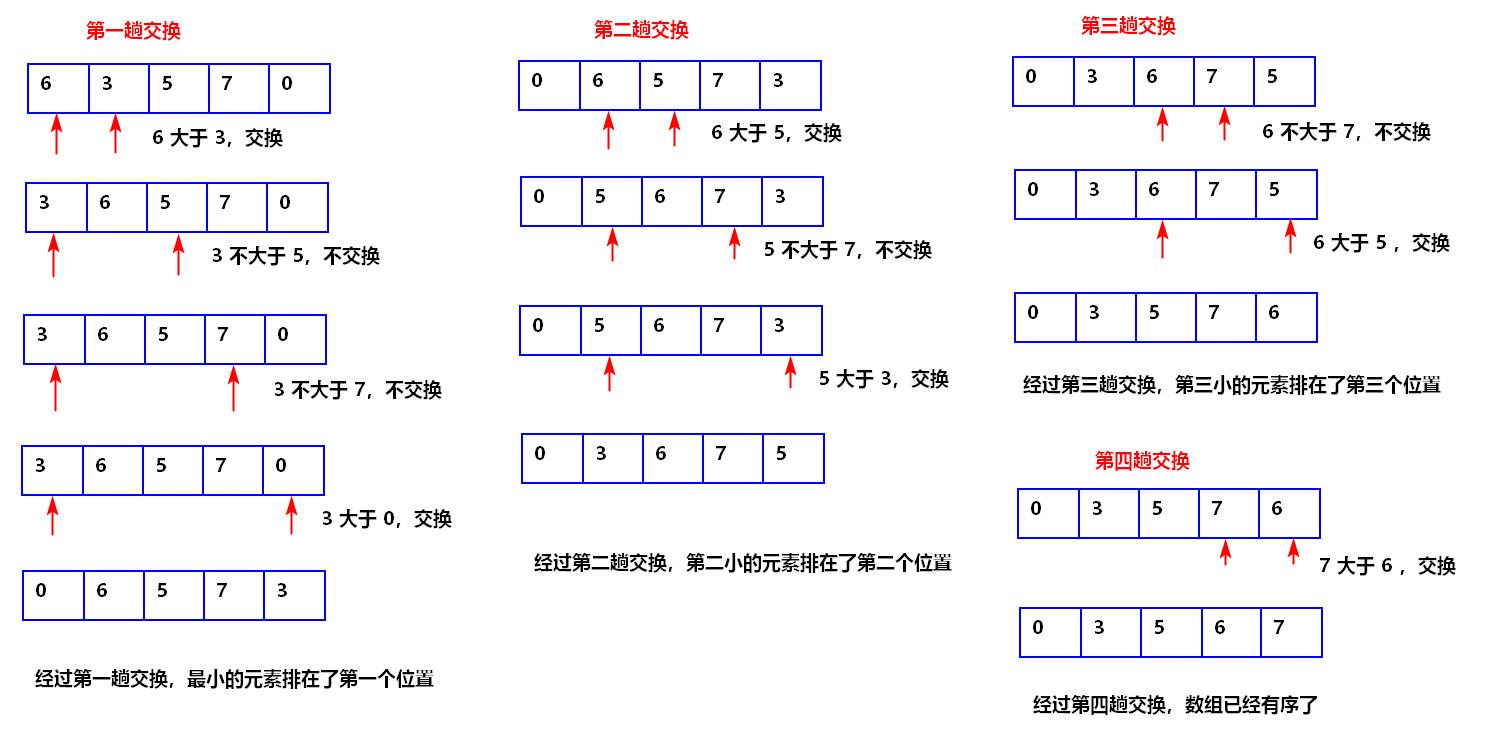
堆排序

堆排序是什么呢？那我们先了解堆是什么，在了解堆是什么之前，先了解什么是树。什么是二叉树。这些名词的提出，是不是把大家吓坏了。其实这个很好理解。

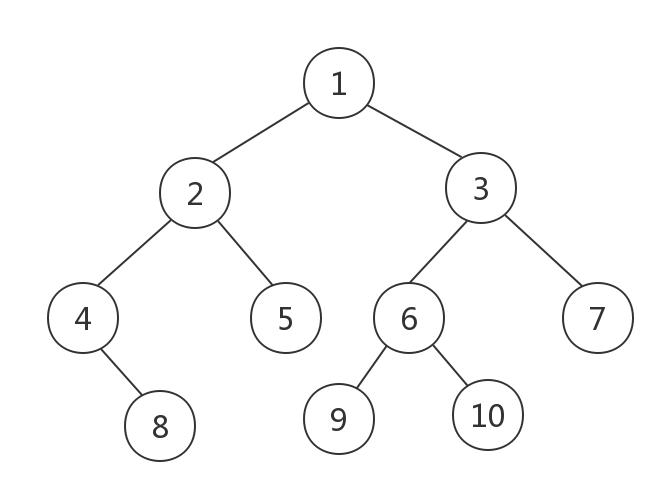
形状像这样的就是二叉树。就是每一个节点下面都有两个节点。每个初始节点就像家长一样，底下两个就是他的孩子
那什么是堆呢？
就是二叉树的一部分

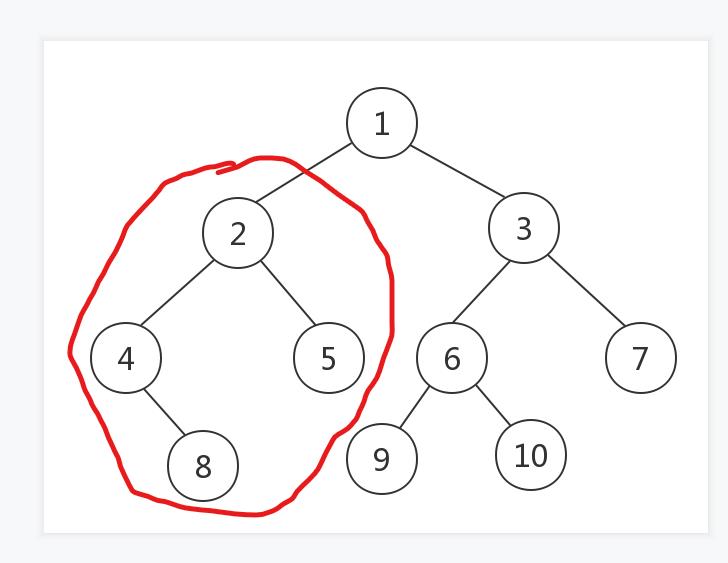
红圈标识的就是堆。
其实堆排序体现了分治的思想。就是把大问题分解成一个个小问题。然后解决小问题，最后解决大问题。
话不多说
先看代码

void Swap(int* a, int* b)
{
	int t = 0;
	t = *a;           //这个函数用来交换
	*a = *b;
	*b = t;
}
void AdjustDwon(int* a, int n, int root)
{
	int parent = root;    //先确定家长
	int child = parent * 2 + 1;  //利用家长节点求出孩子节点。这个地方的寻找是有公式的。公式就是这个表达式。不过这个求出来的是左孩子，右孩子要加1；
	while (child<n)
	{
		if (child < n-1 && a[child + 1] > a[child]) //这边就是让一个个小堆能有序。
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);  
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int* a, int n)
{
	for (int i = (n - 2) / 2; i >= 0; i--)
	{
		AdjustDwon(a, n, i);
	}
	//排升序建大堆。那么什么是大堆呢？那就是孩子小于家长，右孩子大于左孩子；小堆相反。
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDwon(a, end, 0);   //实现排序的实现。
		--end;
	}
}

堆排序的思想比较抽象，而且要一定的代码储备量；为了更好的理解，我也配上了图：

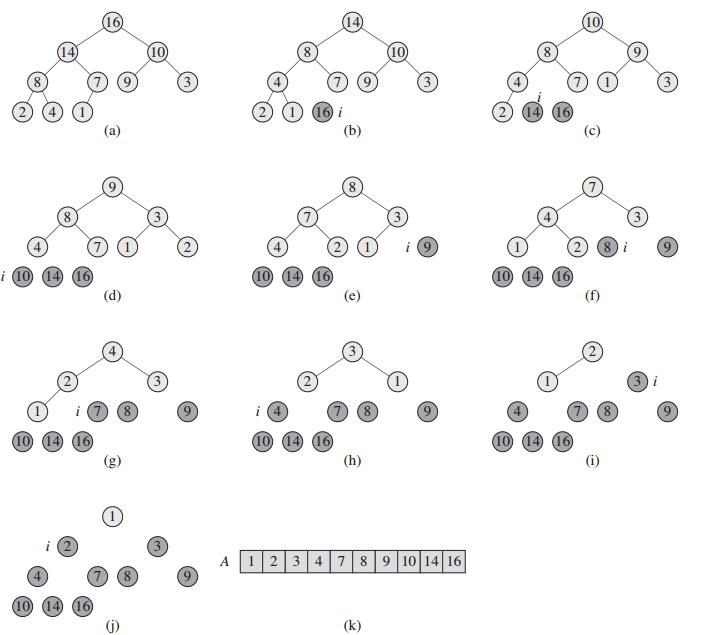
冒泡排序

这个排序型如其名。是一个一个跟身边的比较，然后实现排序的。
话不多说，先上代码：

void popSort(int* a, int n)
{
	int i = 0;   //用于控制趟数；
	int j = 0;    //用于控制比较的两个数字
	int t = 0;    //用于交换
	for (i = 0; i < n - 1; i++)
	{
		for (j = 0; j < n - i - 1; j++)
		{
			if (a[j] > a[j + 1])        //用前一个和后一个比较，就像泡泡一样逐步变大。
			{
				t = a[j];  
				a[j] = a[j + 1];    //交换的代码
				a[j + 1] = t;
			}
		}
	}
}

这个代码像直接插入，直接选择一样是比较简单的代码，同样，这三者的时间复杂度类似。都是O(n^2);
图片如下：

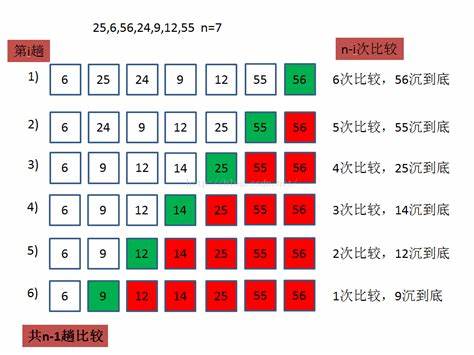
快速排序

快速排序如他的名字一样十分快速。
快到什么地步呢？
代码详见

void QuickSort(int* a, int left ,int right)
{
	if (left >= right)  //判断是不是只有一个元素了
	{
		return;
	}
	int begin = left, end = right;
	int pivot = begin;
	int key = a[begin];   //选出关键值
	while (begin < end)
	{
		while (begin < end && a[end] >= key)  //观察关键值和最后一个值的大小关系。
		{
			end--;
		}
		a[pivot] = a[end];
		pivot = end;
		while (begin < end && a[begin] <= key)  //观察关键值和最开始一个值的大小关系。
		{
			begin++;
		}
		a[pivot] = a[begin];
		pivot = begin;
	}       //以上两个比较都是为了，关键值的左边都是小于他的，右边都是大于他的。
	pivot = begin;
	a[pivot] = key;
	QuickSort(a, left, pivot - 1);    //这边用到了递归和分治的思想。
	QuickSort(a, pivot + 1, right);
}

快速排序的大体就是利用关键值的左边都是小于他的，右边都是大于他的。然后形成升序。
图片：

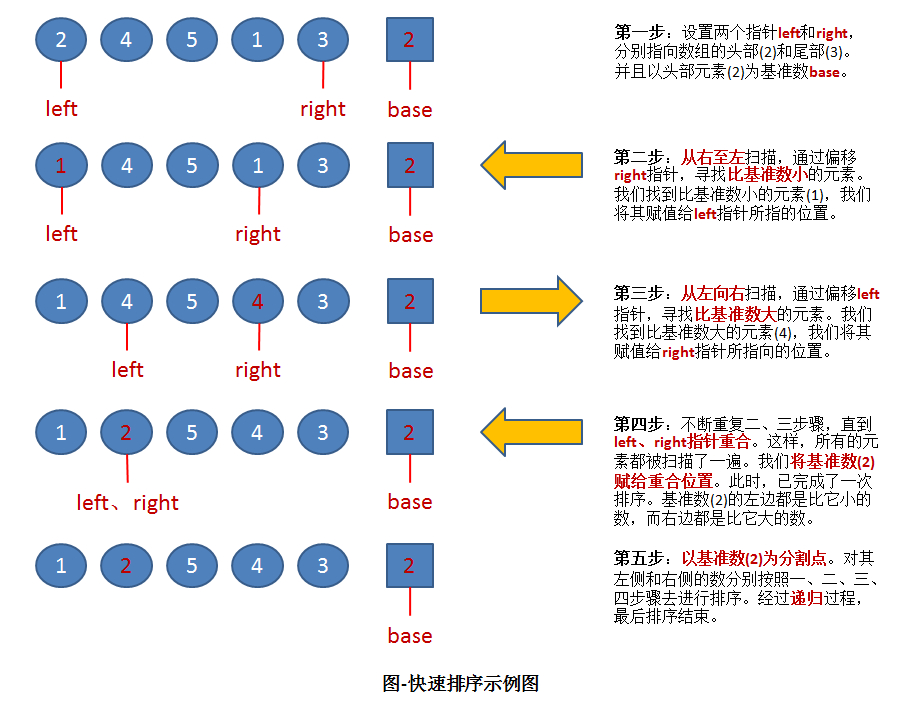
快速排序有三种变形。这个我们下次分享。
剩下的两种排序，我将会在下个文章里面介绍一下。
最后感谢大家的阅读，如果有帮到你，那是我的荣幸。谢谢大家的支持。我就怕我哪边没解释清楚，最后误人子弟。如果有不懂的也可以问我。我有空一定回复。最后，让我们一起成长吧！！！！